有一类螺旋槽的轴向剖面呈半圆形(如滚珠丝杠和滚珠丝杠螺母上的螺旋槽)。这类螺旋槽在半径较小时,常采用半圆头成形车刀(包括装圆刀片的可转位车刀和手工刃磨的车刀)车削。下面讨论用半径与槽半径相同的车刀进行粗车的等截面积切削(见图2-16)数据。
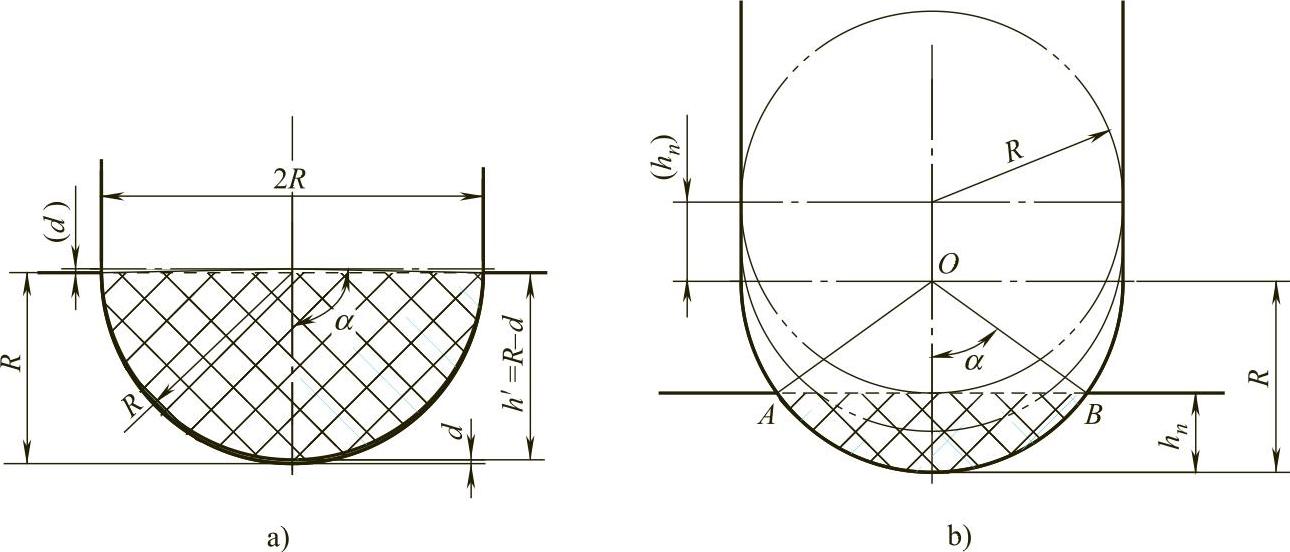
图2-16 半圆形螺纹的等截面积切削
a)半圆形螺纹的粗车总截面积 b)半圆形螺纹的某刀累计切去面积
如图2-16a所示,先计算粗车应切去的总面积S3和粗车各刀应切去的面积S4。
当圆半径为R时,半圆面积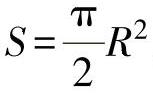 。
。
确定精车留量d后,粗车总深h′=R-d。
扇形半角 。
。
扇形面积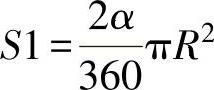
等腰三角形面积S2=dRsinα
粗车总面积S3=S1-S2。
如果N=10,即分10刀车,则每刀应车面积S4=S3/N。
第n刀累计切去的面积Sn=nS4。
【例3】当槽和刀的R都等于5mm时:
半圆面积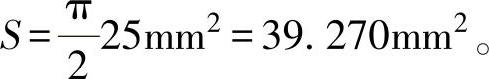
如确定精车留量d=0.04mm,那么粗车总深h′=R-d=4.96mm。
扇形半角
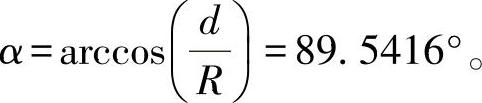
扇形面积

等腰三角形面积S2=dRsinα=0.04mm×5mm×sin89.5416°=0.2mm。
粗车总面积S3=S1-S2=38.87mm2。
如果N=10,即分10刀车,每刀应车面积S4=S3/N=3.887mm2。
第n刀累计切去的面积Sn=nS4=3.887n。
那么10刀切去的累计面积应分别为:
S1=3.887mm2
S2=7.774mm2
S3=11.661mm2
S4=15.548mm2
S5=19.435mm2
S6=23.322mm2
S7=27.209mm2
S8=31.096mm2
S9=34.983mm2
S10=38.87mm2
下面推导第n刀累计背吃刀量hn与累计切去面积Sn的关系式(见图2-16b)。
等腰三角形OAB的面积

扇形半角

扇形面积 。
。
阴影面积Sn=S1-S2。

这就是第n刀累计背吃刀量hn与累计切去面积Sn的关系式。
第n刀累计切去面积又等于nS4(每刀切去面积),所以有

用普通数学解这个方程(即求累计背吃刀量hn与刀序n的关系)有困难。
下面介绍两种方法来得到各刀的累计背吃刀量。
第一种是用作圆法来获取各刀累计背吃刀量的近似值。以半径等于5mm、精车留量取0.04mm、共10刀粗车的例子来说明具体的做法。
如图2-17a所示,例子中的AB长4.96mm。此法分两步。第一步是作各刀背吃刀量h与切去面积S之间的关系曲线。先为作曲线准备一组(10对)数据。把线段AB平移复制到右侧,成为线段CD。从C点向右作一段长度等于CD的水平线CE,并连接D、E两点。直接用作图法把∠CED10等分。这9条等分线与CD线有9个交点。从这9个交点和C点作水平线与AB线相交,生成10个交点(含A点)。依次标注出各交点与B点之间的距离,此距离即为10个累计背吃刀量(注意此时尚不是等截面积)。把这10点作为下象限点作10个R5mm半圆,再用“查询”工具查得这10个半圆在BD线之下(即累计切去)的面积。图中的S1~S10是查得的数据。这样就可得到依次10个累计背吃刀量和依次10个切去面积组成的10组数据。
再作关系曲线,如图2-17b所示。面积S作为横坐标轴,各刀背吃刀量h作为纵坐标轴,建立一个直角坐标系。用刚得到的10组数据作图可得到10个交点,用作图中的“样条”从零点开始依次连接这10个点,就可得到各刀背吃刀量h与切去面积S之间的关系曲线。
第二步是利用刚才得到的关系曲线来获取等截面积切削条件下的各刀背吃刀量。如图2-18所示,先把图2-17b复制过来,删去20条细实线和20个数据,仅保留坐标轴和关系曲线,用前面算得的等截面积切削条件下10刀应切去面积值作为横轴上的10个点,通过这10个点作铅垂线与曲线相交,再通过这10交点作水平线与纵坐标轴相交,标出纵坐标轴上10个点对应的h值,即为等截面积切削条件下10刀各自的累计背吃刀量。此数据精度可达0.01mm,在此已足够了。
这种作图法叙述起来好像较复杂,但实际做起来很简单,也很快。(https://www.xing528.com)
第二种是用宏程序协助计算来获取各刀累计背吃刀量的近似值。
O201程序是作者开发出的可直接用于这种计算的宏程序。使用时,只要把槽半径(即刀头半径)R、精车留量d和粗车刀数这3个数据分别赋给变量#1、#2和#3后运行,就可以从#131~#140变量位逐个查询得到各刀的累计背吃刀量。所编程序数据的精度也是0.01mm,足够使用。

图2-17 作各刀背吃刀量h与切去面积S之间的关系曲线
a)为作各刀背吃刀量h与切去面积S之间的关系曲线准备数据 b)利用a图中所得数作h=f(s)的关系曲线

图2-18 用h与S的关系曲线获取各刀的累计背吃刀量
图2-19所示为用图2-16所示半圆形螺纹的3个已知数据代入O201程序后的运行结果,图中右侧最下部的#131~#140位上显示的就是第1~10刀依次的累计背吃刀量。
下面对O201宏程序做简单介绍,供有兴趣的读者参考。
此宏程序由四部分组成。N1~N3为第一部分,赋已知条件的值。N10~N22为第二部分,先把粗车总深均分500档(段),再计算各档(刀)的累计切去面积,并依次存入#500~#999变量内,本例中每段的长度为0.0092mm。图2-19中显示的#982~#999值是最后18档的累计切去面积。N30~N34为第三部分,用于计算在等截面积切削条件下各刀应切去的累计面积,并将其分别存入变量#101~#110中(结果在图2-19中)。N40~N53为第四部分,是找出等截面积切削条件下多刀的累计背吃刀量(精确到0.01mm),并将其存在#131开始的变量中。
第四部分分两步。第一步是分别找出与等截面积切削条件下各刀应切去面积最接近的档面积对应的档序号,该任务由N44~N50段内循环完成;第二步是依次算出这10个档序号对应的累计背吃刀量,该任务由N41~N53段外循环完成。
此宏程序的原理有一定的普遍适用性。至于手段,可以用宏程序,也可以c语言或别的高级语言程序。用c语言等高级语言编制的程序在计算机上的运算速度更快。
O201;
N1 #1=5; (#1代表槽的半径和车刀刀头半径R,是已知条件,本例中为5mm)
N2 #2=0.04; (#2代表精车留量d,是已知条件,本例中为0.04mm)
N3 #3=10; (#3代表粗车总刀数N,是已知条件,本例中为10)
N10 #4=500; (#4代表粗车总深分档数N2,此值仅用于计算)
N11 #5=1; (#5代表第n档,赋初始值1)
N12 #6=[#1-#2]/#4; (#6代表每档的深度Δh值)
N13 #7=#6; (#7代表本档的深度hn值,赋初始值)
N14 WHILE[#5LE#4]DO1; (计算各档累计面积循环的循环头)
N15 #8=ACOS[[#1-#7]/#1]; (#8代表本档的扇形半角α)
N16 #9=3.1416∗#1∗#1∗#8/180; (#9代表本档的扇形面积S1)
N17 #10=[#1-#7]∗#1∗SIN[#8]; (#10代表本档的等腰三角形面积S2)
N18 #11=#9-#10; (#11代表本档的累计切削面积S3)
N19 #[499+#5]=ROUND[#11∗1000]/1000; (把各档的累计切削面积存起来)
N20 #7=#7+#6; (深度h增加一个档深Δh)
N21 #5=#5+1; (档序号增加1)
N22 END1; (计算各档累计面积循环的循环尾)
N30 #100=#999/#3; (把粗车总面积转存入#100变量中)
N31 #12=1; (#12代表粗车分刀序号,赋初始值)
N32 #[100+#12]=ROUND[#100∗#12∗1000]/1000; (把本刀的累计应切面积存起来)
N33 #12=#12+1; (粗车分刀序号增加1)
N34 IF[#12LE#3]GOTO32; (如果粗车分刀序号不超过粗车总刀数N,那么返回执行N32段)
N40 #12=1; (#12代表粗车分刀序号,此重赋初始值)
N41 WHILE[#12LE#3]DO3; (算出与本刀应切面积最接近那个数对应的档序号所对应的切削深度循环的循环头)
N42 #5=1; (#5代表第n档,重赋初始值1)
N43 #13=1000000; (#13代表一个库,在库里预存一个足够大的值)
N44 WHILE[#5LE#4]DO2; (寻找与本刀应切面积最接近那个数对应的档序号循环的循环头)
N45 #14=#[499+#5]; (把本档的累计切削面积存放到#14变量中)
N46 IF[ABS[#14-#[100+#12]]LTABS[#14-#13]]THEN#13=#14; (找500个数中与本刀应切面积最接近的数)
N47 IF[#14EQ#13]THEN#15=#5; (#15代表与本刀应切面积最接近那个数对应的档序号)
N48 IF[#13GT#14]GOTO51; (如算出的本档累计切削面积已比库里的大,就跳出循环)
N49 #5=#5+1; (档序号增加1)
N50 END2; (寻找与本刀应切面积最接近那个数对应的档序号循环的循环尾)
N51 #[130+#12]=ROUND[#15∗#6∗1000]/1000; (计算并存储与本刀应切面积最接近那个数的档序号对应的切削深度)
N52 #12=#12+1; (粗车分刀序号增加1)
N53 END3; (算出与本刀应切面积最接近那个数的档序号对应的切削深度循环的循环尾)
N99 M00;

图2-19 半圆形螺纹的等截面积切削宏程序计算结果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




