短路电流热效应的优化处理

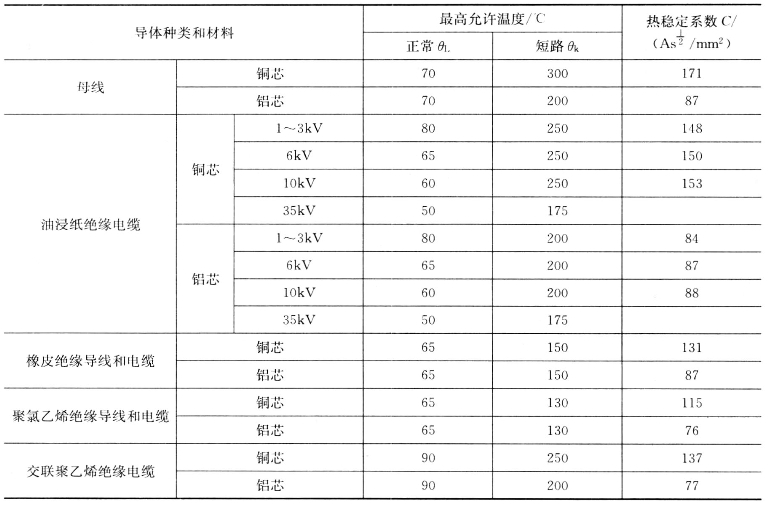
当系统发生短路故障时，通过导体的电流要比正常工作电流大很多倍。虽然继电保护装置能在很短的时间内切除故障，但导体的温度仍有可能被加热到很高的程度，导致电气设备的损坏。如果导体在短路时的最高温度不超过设计规程规定的允许温度（见表4-6），则认为导体是满足热稳定要求的。所以短路时发热计算的目的是确定导体在短路时的最高温度，再与该类导体在短路时的最高允许温度相比较。

表4-6　导体在正常和短路时的最高允许温度及热稳定系数

1.短路时导体发热计算的特点

1）由于短路时间很短，温度上升速度很快，可以认为短路过程是一个绝热过程，即短路电流产生的热量不向周围介质散发，全部用来使导体的温度升高。

2）由于导体的温度上升得很高，不能把导体的电阻和比热容看成常数，而是随温度而变化的。

3）由于短路电流的变化规律复杂，要想把短路电流在导体中产生的热量直接计算出来是很困难的，通常用等效发热的方法进行分析计算。

2.短路时导体的发热计算

图4-27表示短路前后导体的温度变化情况。导体在短路前正常负荷时的温度为，设在时刻发生短路，导体温度按指数规律迅速升高，在时刻保护装置动作将故障切除，这时导体的温度为。短路切除后，导体内无电流，不再产生热量，只向周围介质散热，最后冷却到周围介质温度θ0。

要确定短路后导体的最高温度，就必须先求出实际的短路电流或在短路时间内产生的热量，即

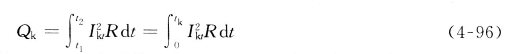
式中，为短路全电流的有效值（A）；R为导体的电阻（Ω）；为短路电流作用时间（s）。

由于短路电流的变化规律比较复杂，按式（4-96）计算相当困难，因此一般用稳态短路电流来代替实际短路电流，并设定一个假想时间，认为短路电流在短路时间内产生的热量，恰好等于稳态短路电流在假想时间内产生的热量，即

式中，为假想时间，如图4-28所示。

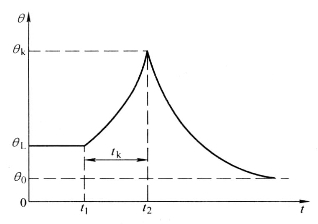
图4-27　短路前后导体的温度变化

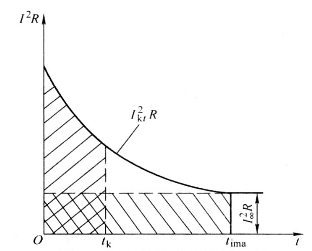
图4-28　短路发热的假想时间

（1）假想时间的计算　假想时间与短路电流的变化特性有关。短路电流分为周期分量和非周期分量，根据式（4-28），短路电流的有效值可表示为

代入式（4-97），便有

设假想时间也分为相应的周期分量假想时间和非周期分量假想时间，即

则有

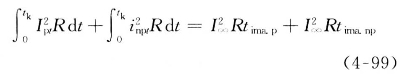
根据式（4-99），周期分量假想时间可表示为

令系数，可根据短路电流周期分量的变化曲线作出β"与的关系曲线，如图4-29所示，则周期分量假想时间可按t查曲线求出。

当短路点离电源较远时（无限容量系统），可认为，因此周期分量假想时间就等于短路的延续时间，即。等于距离短路点最近的保护装置的实际动作时间和断路器的跳闸时间之和。对于快速和中速断路器，可取；低速断路器，可取。

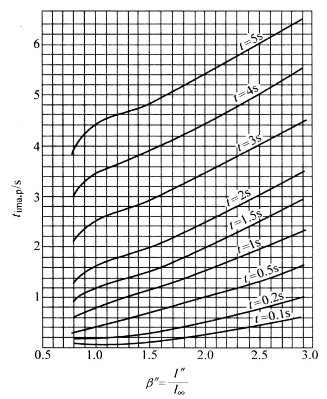
图4-29　β"与的关系曲线

短路电流非周期分量假想时间只有在短路时间较短时才考虑，可用下式表示：

由于

将平均值及t=0.1s代入上式得

在无限容量系统中，β"=1，故。总的假想时间为

（2）短路时导体的最高温度　由于短路时间很短，可认为短路电流产生的热量全部用来使导体的温度升高，而不向周围介质散热，则热平衡方程式可表示为

式中，G为导体的质量；A为导体的截面；l为导体的长度；为导体材料的密度；c为导体材料的比热容；为导体在短路时间内的温升。

式（4-104）可表示为

故(https://www.xing528.com)

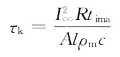
设令，则上式变为

因此，短路时导体的最高温度为

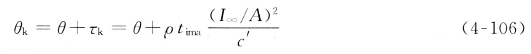
由于导体的电阻率ρ和比热容c是随温度而变化的，因此导体的最高温度很难直接计算出来，工程上多采用查曲线的近似方法计算。图4-30是按铜、铝、钢的比热容、密度、电阻率等的平均值作出的K=f（θ）曲线，横坐标为导体加热系数K，纵坐标为导体温度θ。

（3）根据曲线确定的方法（见图4-31）

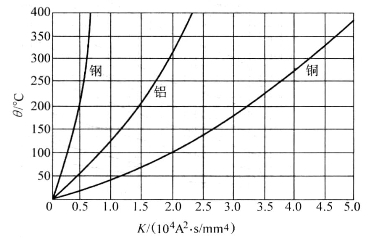
图4-30 用来确定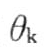的曲线

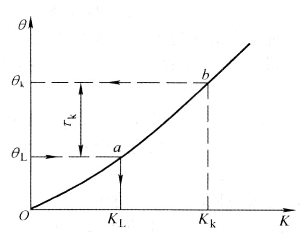
图4-31　根据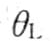确定的步骤

1）根据正常负荷电流确定短路前导体的温度；如果难以确定，可选用导体材料的正常最高允许温度。

2）在纵坐标上查出值，并向右在对应的材料曲线上查出a点，再由a点在横坐标上查出加热系数。

3）利用下式计算短路时的加热系数：

式中，A为导体的截面（mm2）；为三相短路稳态电流（A）；为假想时间（s）；和分别为正常和短路时的加热系数（A2·s/mm4）。

4）从横坐标上找出的值，并向上在对应的曲线上查出b点，再由b点向左在纵坐标上查出值。

3.短路时的热稳定校验

（1）一般电器的热稳定校验　一般电器满足热稳定的条件为

式中，为电器的热稳定试验电流；t为电器的热稳定试验时间（s）。

（2）母线、绝缘导线及电缆的热稳定校验　满足热稳定的条件为

式中，为导体在短路电流通过时的最高允许温度，可查表4-6。

由于计算短路时导体的最高温度比较麻烦，因此也可根据热稳定条件计算导体的最小允许截面。由式（4-107）得

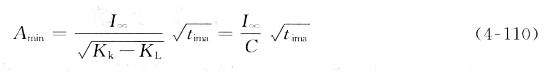
式中，C为导体的热稳定系数，可查表4-6；为三相短路稳态电流（A）。

只要所选导线截面A＞Amin，热稳定就能满足要求。

例4-4　已知某降压变电所低压侧10kV母线上的短路电流为，继电保护动作时间，断路器分闸时间，采用矩形母线平放布置，母线的相间距离s=250mm，母线支持绝缘子的跨距l=1m，跨距数大于2，母线的工作电流。试选择母线截面并进行短路的动稳定和热稳定校验。

解：（1）截面选择　根据，在附录表A-9中选择矩形50mm×5mm的铝母线。

（2）热稳定校验　短路电流的假想时间为

查表4-6得，铝母线的热稳定系数，因此最小允许截面为

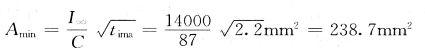
实际选用的母线截面A=50mm×5mm=250mm2＞Amin，所以热稳定满足要求。

（3）动稳定校验　10kV母线三相短路时的冲击电流为

1）确定母线截面形状系数：由于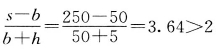，故K≈1。

2）母线受到的最大电动力为

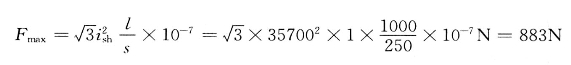
3）母线的弯曲力矩为

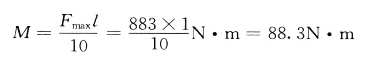
4）母线的截面系数为

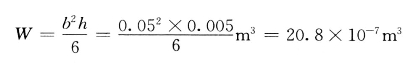
5）母线的计算应力为

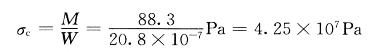
铝母线排的最大允许应力，所以动稳定满足要求。