电力系统简单不对称短路有单相接地短路、两相短路和两相接地短路。为了简化计算,假定短路是金属性的,即不计短路点的弧光电阻和接地电阻。无论是哪一种短路,利用对称分量法,都可按式(4-54)写出短路点各序网的电压方程。式(4-54)的三个方程式中包含了六个未知量。因此,还需根据不对称短路的边界条件列出另外三个方程式,才能进行求解。
1.单相接地短路
图4-14表示a相接地短路,短路点的边界条件为
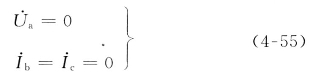
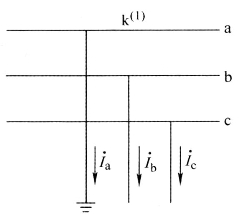
图4-14 单相接地短路
将式(4-55)转换为对称分量的形式,并经整理后可得用序分量表示的边界条件为
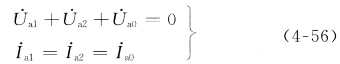
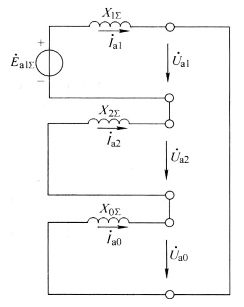
图4-15 单相接地短路的复合序网
将基本序网方程式(4-54)和边界条件方程式(4-56)联立求解,可得短路点的正序分量电流为
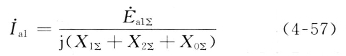
式(4-57)还可根据复合序网求得。所谓复合序网,是指根据边界条件所确定的短路点各序之间的关系,由各序网络互相连接起来所构成的网络。由式(4-56)可见,由于各序电流相等,所以正序网、负序网、零序网应互相串联;同时因各个序量电压之和等于零,故三个序网串联后应短接。这就决定了单相接地短路时的复合序网如图4-15所示。显然,由此网络可直接得到式(4-57)。
从图4-15可得到短路点电流和电压的各序分量为
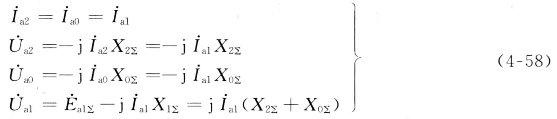
短路点的故障相电流为
![]()
则单相接地短路电流为
![]()
短路点非故障相对地电压为
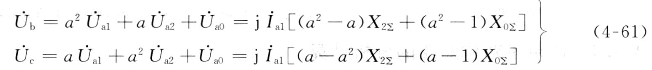
图4-16为单相(a相)接地短路时短路点的电压和电流相量图。图中以正序电流![]() 为参考相量,
为参考相量,![]() 与
与![]() 大小相等、方向相同,
大小相等、方向相同,![]() 超前
超前![]() ,而
,而![]() 和
和![]() 0均滞后
0均滞后![]() 。图中示出的电压相量关系对应的是
。图中示出的电压相量关系对应的是![]() 的情况,此时
的情况,此时![]() 与
与![]() 的夹角
的夹角![]() 。
。
2.两相短路
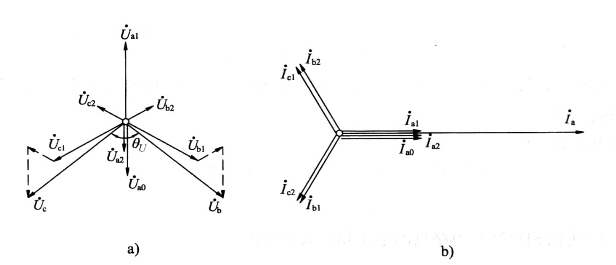
图4-16 单相接地短路时短路点的电压和电流相量图
a)电压相量图 b)电流相量图
图4-17表示b、c两相短路的情况,短路点的边界条件为

将式(4-62)转换为对称分量的形式,并经整理后可得用序分量表示的边界条件为

由式(4-63)可见,由于![]() ,所以零序网络开路;又因
,所以零序网络开路;又因![]() ,所以两相短路的复合序网是由正序网和负序网并联而成的,如图4-18所示。
,所以两相短路的复合序网是由正序网和负序网并联而成的,如图4-18所示。
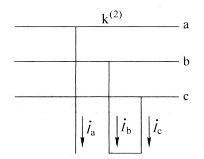
图4-17 两相短路
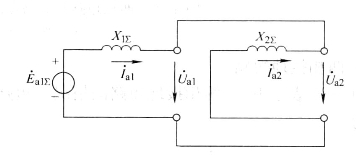
图4-18 两相短路的复合序网
根据复合序网,可得两相短路时短路点电流和电压的各序分量为
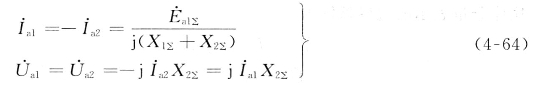
短路点的故障相电流为
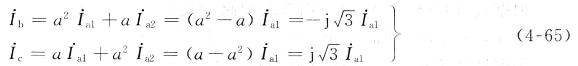
当在远离发电机的地方发生两相短路电流时,可认为![]() ,两相短路电流为
,两相短路电流为
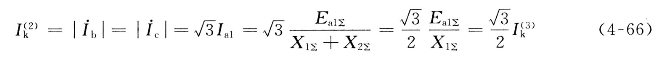
式(4-66)表明,当![]() (故障点远离电源)时,两相短路电流为同一地点三相短路电流的
(故障点远离电源)时,两相短路电流为同一地点三相短路电流的![]() 倍。(https://www.xing528.com)
倍。(https://www.xing528.com)
短路点各相对地电压为
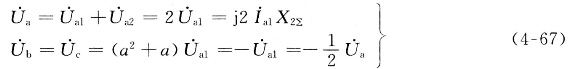
图4-19为两相短路时短路点的电压和电流相量图。
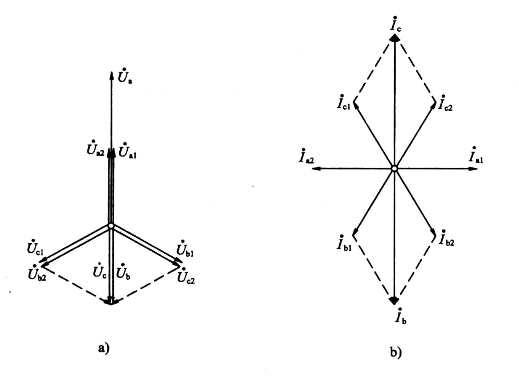
图4-19 两相短路时短路点的电压和电流相量图
a)电压相量图 b)电流相量图
3.两相接地短路
图4-20表示b、c两相接地短路的情况,短路点的边界条件为
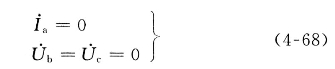
将式(4-68)转换为对称分量的形式,并经整理后可得用序分量表示的边界条件为
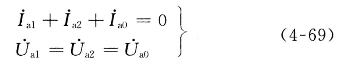
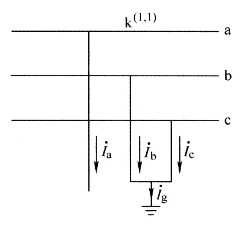
图4-20 两相接地短路
根据式(4-69)可作出两相接地短路的复合序网如图4-21所示,它是由正序网、负序网和零序网并联而成的。
根据复合序网,可得两相接地短路时短路点电流和电压的各序分量为
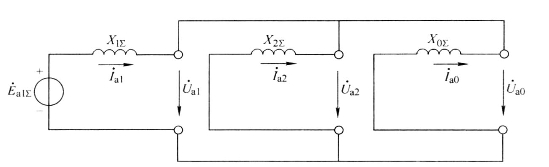
图4-21 两相接地短路的复合序网
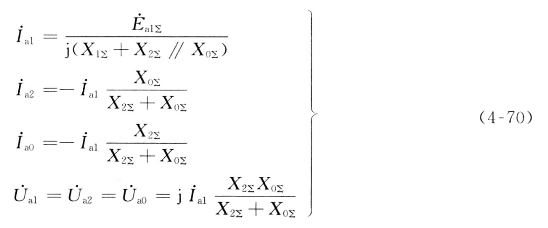
短路点的故障相电流为
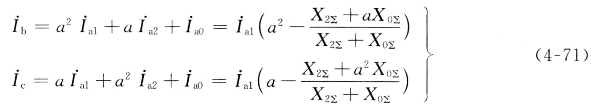
则两相接地短路电流为
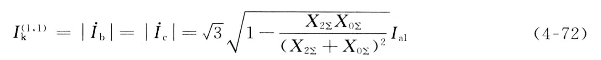
两相接地短路时,流入地中的电流为

短路点非故障相电压为
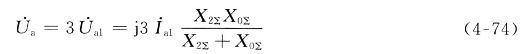
图4-22为两相接地短路时短路点的电压和电流相量图。图中示出的电流相量关系对应的是![]() 的情况,此时
的情况,此时![]() 与
与![]() 的夹角
的夹角![]() 。
。
4.正序等效定则
观察以上各种不对称故障时的正序电流计算式可知,故障相正序电流绝对值![]() 可用以下通式表示:
可用以下通式表示:

式中,![]() 为对应短路类型(n)的附加电抗。
为对应短路类型(n)的附加电抗。
式(4-75)表明,在简单不对称短路的情况下,短路点的正序电流分量,与在短路点每一相中接入附加电抗![]() 而发生三相短路的电流相等。这就是正序等效定则。
而发生三相短路的电流相等。这就是正序等效定则。
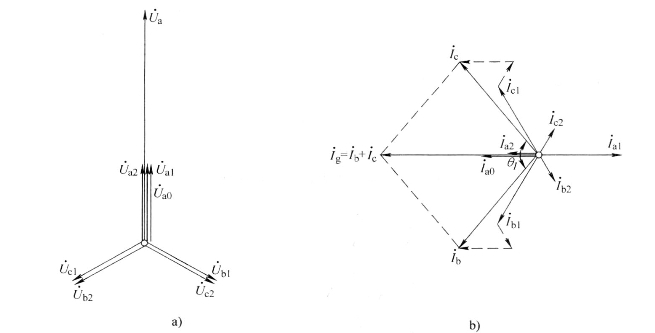
图4-22 两相接地短路时短路点的电压和电流相量图
a)电压相量图 b)电流相量图
此外,各种不对称故障时短路电流的绝对值![]() 与其正序电流的绝对值
与其正序电流的绝对值![]() 成正比,即
成正比,即
![]()
式中,![]() 为比例系数,其值随短路类型而异。
为比例系数,其值随短路类型而异。
各种不同短路类型的附加电抗![]() 和比例系数
和比例系数![]() 见表4-4。
见表4-4。
表4-4 各种短路时的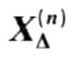 和
和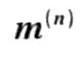 值
值

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




