相关和回归分析：了解变量间关系的方法

在生产过程中，许多现象是互相联系、互相制约的，如果现象A是现象B的原因，则现象B就是现象A的结果。A和B的这种关系叫因果关系。如果不考虑原因和结果的区别，只从现象A与现象B之间有关系而言，这种关系就叫相关关系。

在质量管理中研究两个质量特性之间的关系时，当测定值xi增大时，yi值的平均值也增大，xi减小时，yi值的平均值也减小，那么，x和y之间存在相关关系。如果x和y之间存在函数关系，而这种函数关系又是不确定的，那么，x和y之间存在回归关系，这个函数叫回归函数或回归。

1.相关分析

相关分析是对变量之间的相关关系进行分析，其目的是找出变量之间的相关程度和相关类型。相关分析的主要方法如下。

（1）相关图法。通过相关图（图1-15）可以直观地判断变量之间是否存在相关关系以及相关程度是否密切。同时，还可看出变量之间的相关关系属何种类型的相关。

当一个变量随着另一个变量增加而减少时，为负相关[图1-15（c）]；反之，为正相关[图1-15（b）]。当一个变量随着另一个变量的增加而增加，在到一定程度时又随着另一变量的增加而减小时，称为正负相关[图1-15（d）]。

（2）相关系数法。为了定量地分析变量之间的相关程度，通常采用相关系数法。其计算公式如下：

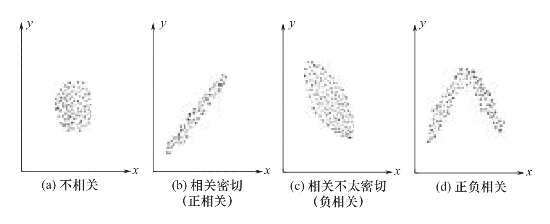
图1-15　相关图

式中：r——相关系数。

可以证明，相关系数r的范围是-1≤r≤1。

当时，则变量之间的相关程度比较密切，越接近1，则相关程度越密切；当r值为正数时，则变量之间的相关关系为正相关，当r值为负数时为负相关。当r值为零时则变量之间是不相关或正负相关。

2.回归分析

回归分析是对变量之间不确定的函数关系进行分析，以便用一个变量来说明另一个变量。如果两个变量之间存在线性函数关系，可用下列直线方程式来表示：

y=a+bx(www.xing528.com)

该直线方程式为y对x的回归方程式。为了使回归直线能够比较准确地反映实际情况，就需要合理地确定a和b，其计算公式如下：

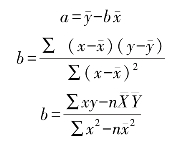
因为回归直线能够比较准确地反映实际情况，可以应用回归直线方程式对产品质量和工程质量进行预测和控制。

例如，经测试获得梳棉机道夫速度与生条棉结杂质的数据如下。

道夫速度（x）18　21　24　27　30　33

棉结杂质（y）30.4　34.7　35.5　36.5　37.5　39.4

求棉结杂质对道夫速度的回归方程式：

首先计算和：

然后计算a和b：

把a和b代入回归方程式，得到棉结杂质对道夫速度的回归方程式为：

y=a+bx=22.49+0.51x

根据这个方程式，在给定道夫速度的情况下，可求出相应的棉结杂质粒数，这为预测和控制棉结杂质提供了理论根据。

回归方程式的应用范围一般应在试验数据范围内（本例中适用于道夫速度在18～33r/min）。如需扩大应用范围，要有理论根据。另外，回归方程式的应用只能由给定x值求相应的y值，而不能由y值求x值。