直方图又称频数分布图,它是进行质量控制的既简便又有效的方法。
1.直方图的用途
(1)直观地分析质量数据集中和离散的情况。
(2)直观地看出各组数据所占的比重。
(3)直观地判断工程质量是否满足质量标准的要求。
例:经测试获得浆轴回潮率的数据见表1-3。
表1-3 浆轴回潮率(%)
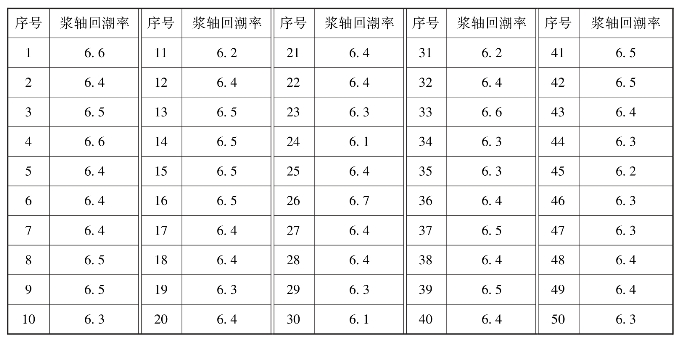
根据以上数据绘制出直方图,如图1-5所示。
从浆轴回潮率直方图可以直观地看出:质量集中情况较好,在靠近平均数6.25~6.5范围内的频数比重占82%,但集中的位置偏离标准中心(下偏),并且距标准下限太近,而距标准上限太远。因此,需要采取措施提高平均数,使其处于标准中心的位置。另外,全部数据都在标准上下限范围以内,说明工程质量能够满足质量标准的要求,在正常的情况下不采取措施也不会产生疵品。
2.直方图的使用与分析
直方图做好后,要检定其分布情况及与标准的差异情况。
(1)看分布形态。直方图一般可分为正常型直方图和异常型直方图两种。正常型直方图的特点是图形呈左右对称的山峰形状,如图1-6所示。异常型直方图情况较多,是注意的重点。异常型直方图的特点是图形左右不对称的山峰形状。
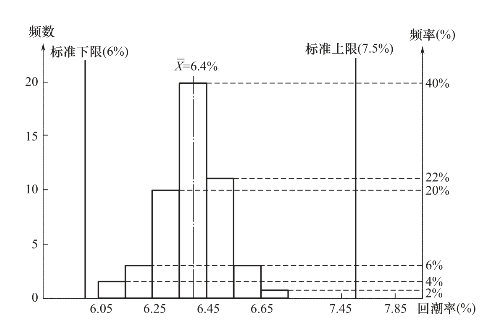
图1-5 浆轴回潮率直方图
(2)将实际分布情况与标准进行比较,判断工程质量是否正常。正常情况是分布图形左右对称,并且图形与标准上下限之间有一定余量,如图1-7所示。(https://www.xing528.com)
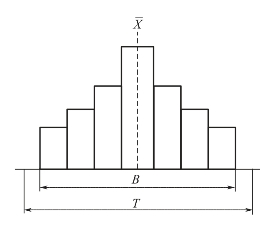
图1-6 正常型直方图
B—产品范围(实际质量差异范围)
T—标准界限(设计标准范围)
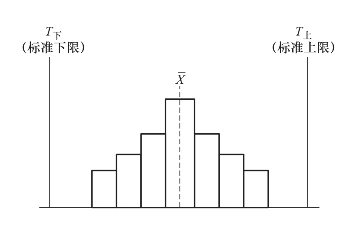
图1-7 正常情况下的直方图
非正常情况有以下几种。
①图形分布与标准上下限之间余量太大或太小,如图1-8所示。
②图形分布与标准上下限之间没有余量,或超出标准上下限,如图1-9所示。
③图形分布偏离标准中心,如图1-10所示。
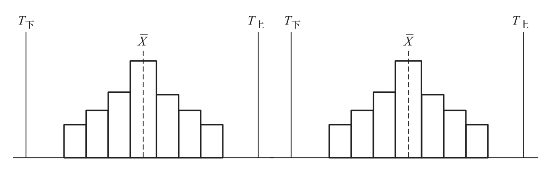
图1-8 非正常情况下的直方图(一)
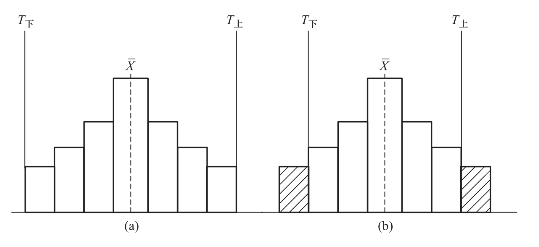
图1-9 非正常情况下的直方图(二)
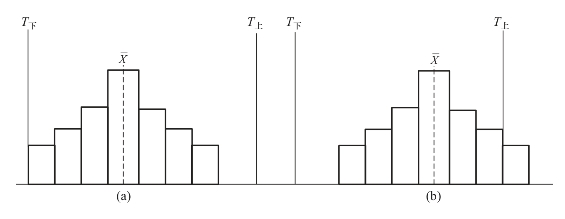
图1-10 非正常情况下的直方图(三)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




