【摘要】：在质量控制中常用的集中性特征数是算术平均数。由上式可得：u的平均值u为：2.离散性特征数离散性特征数表示产品质量离散程度的大小，在质量控制中常用的离散性特征数有极差与均方差。
由于产品质量具有波动性，所以通过随机取样获得的质量数据不会完全一样。为了对产品质量进行分析和判断，就需要用一定的特征数来表示产品质量。
1.集中性特征数
集中性特征数表示产品质量集中的位置或质量水平，如算术平均数、中位数和众数等。在质量控制中常用的集中性特征数是算术平均数。其计算公式如下。
（1）不分组时：
式中：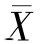
X——算术平均数；
X——随机变量；
f——频数；
n，∑f——总频数。
（2）分组时：
X=X0+cu
式中：X0——基数（一般取频数最大的一组变量值）；
c——组距；
u——随机变量距基数的组距数。(www.xing528.com)
由上式可得：
u的平均值
u为：
2.离散性特征数
离散性特征数表示产品质量离散程度的大小，在质量控制中常用的离散性特征数有极差与均方差。
（1）极差（R）：极差表示产品质量的波动范围，其计算公式如下：
R=Xmax-Xmin
式中：Xmax——随机变量的极大值；
Xmin——随机变量的极小值。
（2）均方差（σ）：均方差表示一批数据的离散程度，其计算公式如下：
不分组时：
分组时：
在质量管理中，为了全面反映产品质量的分布情况，必须同时使用算术平均数，而不能只说明离散情况，极差只能说明产品质量的波动范围，而且不能说明其他各个数据的离散情况。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
