图10.4示意了CBOW的分层网络结构,其中第一层,也就是最上面的那一层称为输入层。输入的是若干个词的词向量,在神经网络概率语言模型中,从隐含层到输出层的计算量是主要影响训练效率的地方,CBOW和Skip-gram模型考虑去掉隐含层。实践证明,新训练的词向量的精确度可能不如NNLM模型(具有隐含层),但可以通过增加训练语料的方法来完善。第三层是方框里面的二叉树,叫霍夫曼树,W代表一个词,Wsyn1代表非叶子结点,是一类词的集合,可以继续分下去。
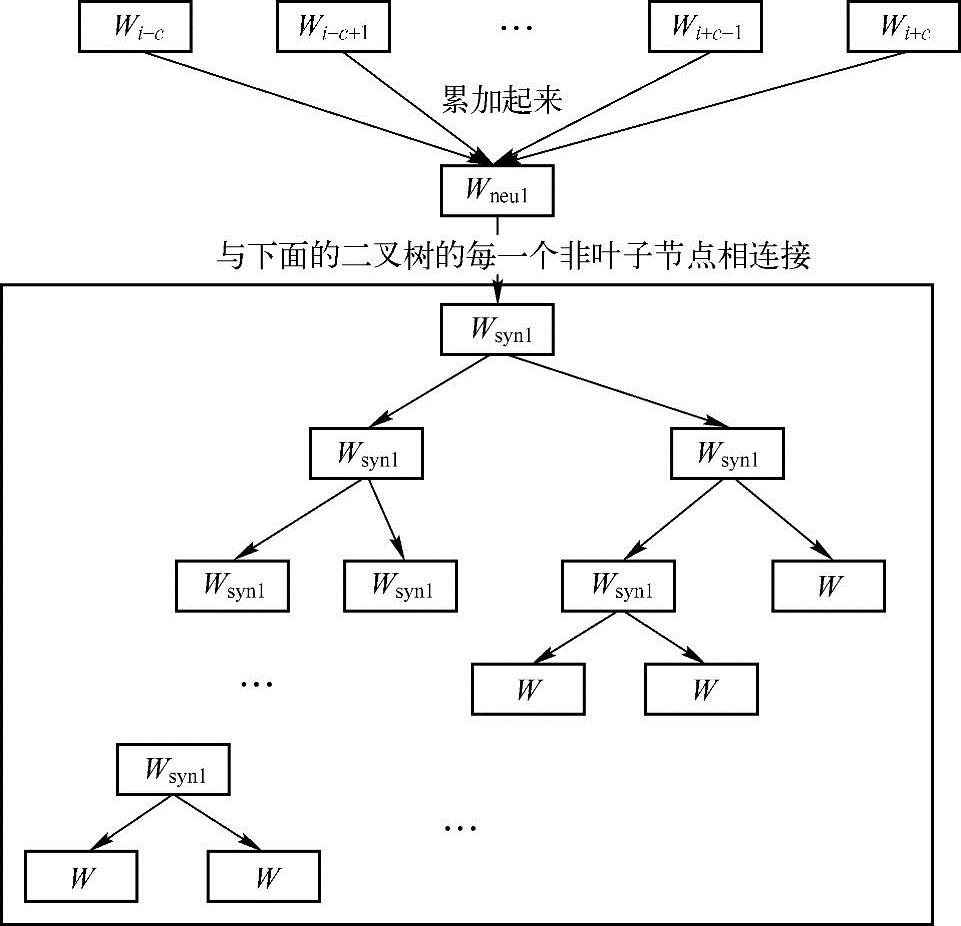
图10.4 HCBOW网络结构
这个网络结构的功能是——判断一句话是否是自然语言。怎么判断呢?使用的是概率,就是计算“一列词的组合”这句话的概率的连乘(联合概率)是多少,如果比较低,那么就可以认为不是一句自然语言,如果概率高,就是一句正常的话。
为描述方便,引入一些记号:
pw:从根结点出发到达w对应结点的路径。
Iw:路径pw中包含结点的个数。
pw1,p2w,…,pwIw:路径pw中Iw个结点。
dw2,dw3,…,dwIw∈{0,1}:词w的霍夫曼编码,它由Iw-1位构成,dwi表示路径pw中第i个结点对应的编码(根结点不对应编码)。
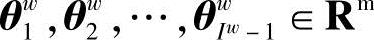 :路径pw中非叶子结点对应的向量,
:路径pw中非叶子结点对应的向量,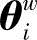 表示路径pw中第i个非叶子结点对应的向量。
表示路径pw中第i个非叶子结点对应的向量。
图10.5显示了霍夫曼编码对应符号解释的例子。
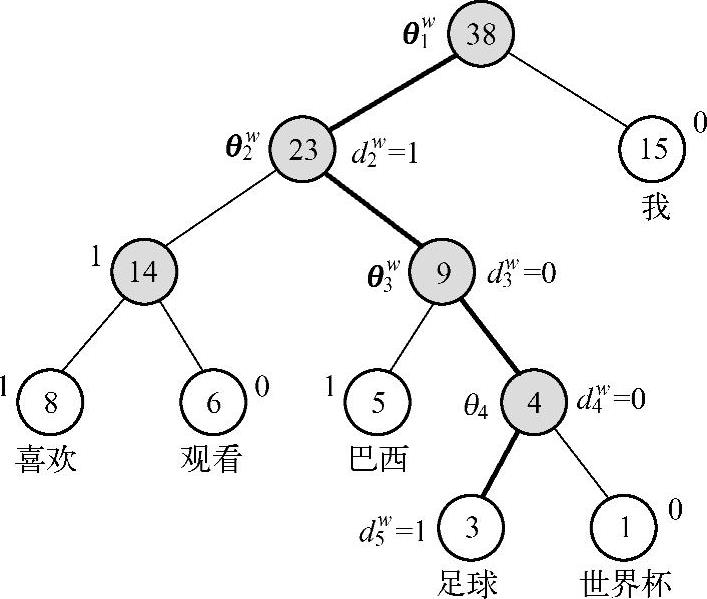
图10.5 霍夫曼编码的例子
以图10.5为例解释引入的记号:w=“足球”,Iw=5,pw1、p2w、pw3、p4w、pw5为路径pw上的5个结点,d2w、dw3、d4w、dw5分别为1、0、0、1,即“足球”的霍夫曼编码1001,θw1、θw2、θw3、θ4w分别表示路径pw上4个非叶子结点对应的向量。
那么,在图10.5所示网络结构下,如何计算p(w|Context(w))?即如何利用向量xw以及霍夫曼树计算p(w|Context(w))。
以图10.5中词“足球”为例,从根结点到达“足球”这个叶子结点,中间经历了4次二分类,左为正类,右为负类。由于一个结点被分为负类的概率为
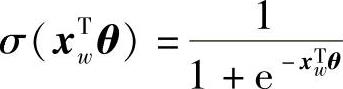
一个结点被分为正类的概率为
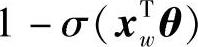
所以,第1次分类概率为
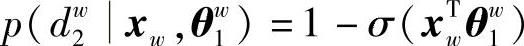
第2次分类概率为

第3次分类概率为
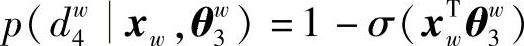
第4次分类概率为(https://www.xing528.com)
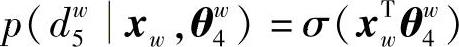
则有

应用HCBOW,需要清楚以下问题:
(1)p(w|Context(w))计算
对字典D中的任意词w,霍夫曼树必存在一条从根结点到词w的唯一路径pw,路径pw上存在Iw-1的分支。将每个分支看作一次二分类,每次分类产生一个概率,将这些概率连乘起来就是所需的概率:
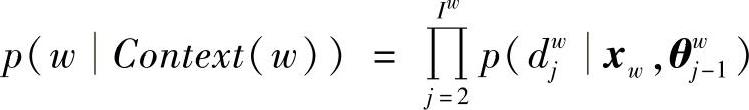
其中
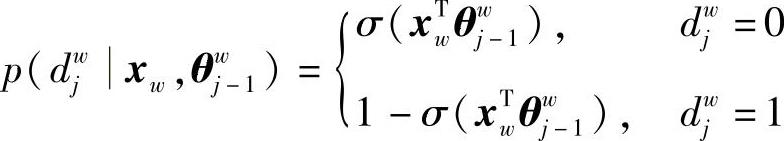
或写成
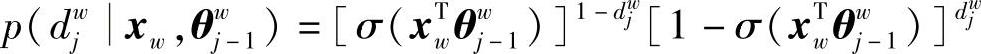
(2)参数修正
对数似然目标函数为
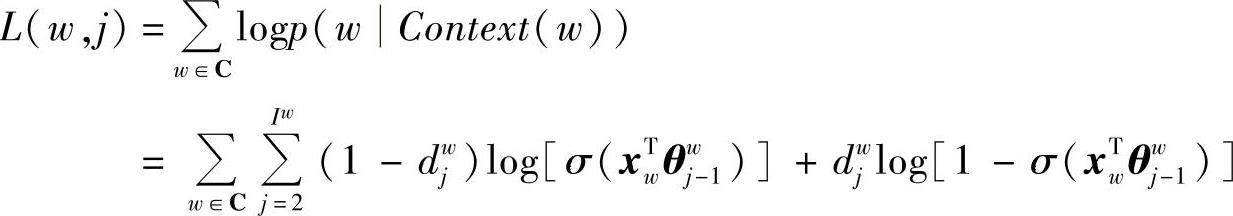
所以,目标函数梯度为
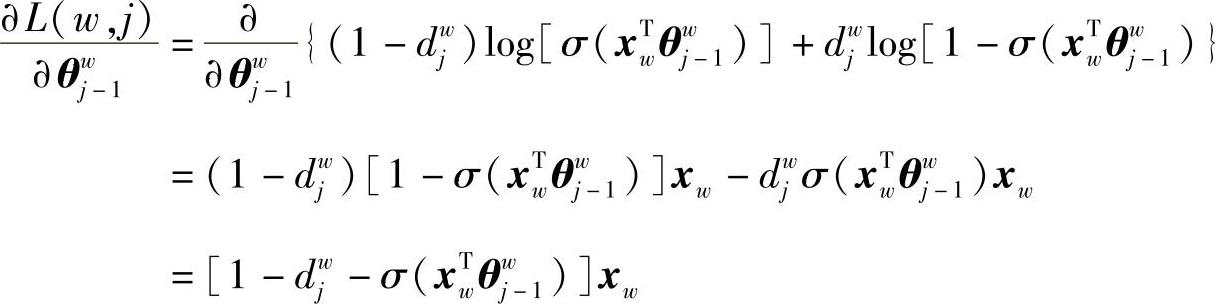
同理,利用L(w,i)中xw和θiw-1的对称性,有
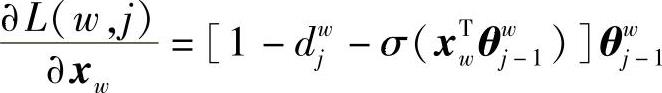
利用随机梯度上升修正参数:θiw的修正公式为
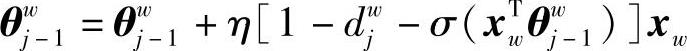
式中,η为学习率。
v(w)的修正公式为
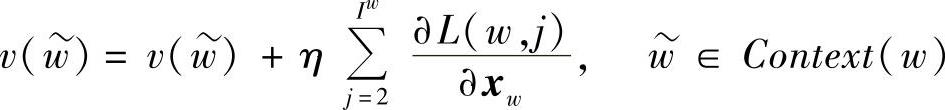
由于xw是v(w)的和,所以要把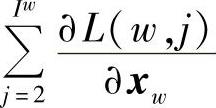 贡献到Context(w)中每一个词向量上。
贡献到Context(w)中每一个词向量上。
(3)伪代码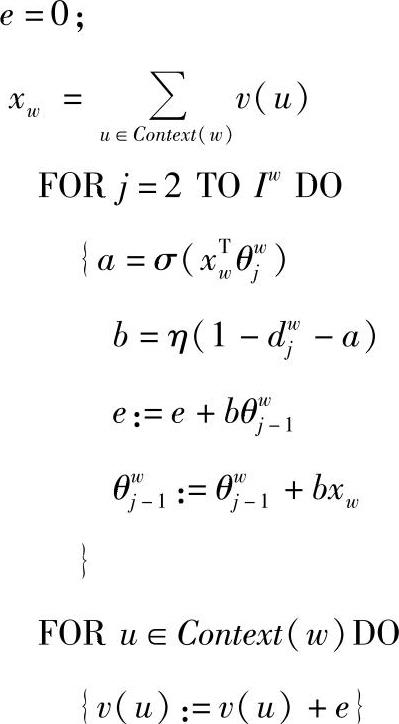
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




