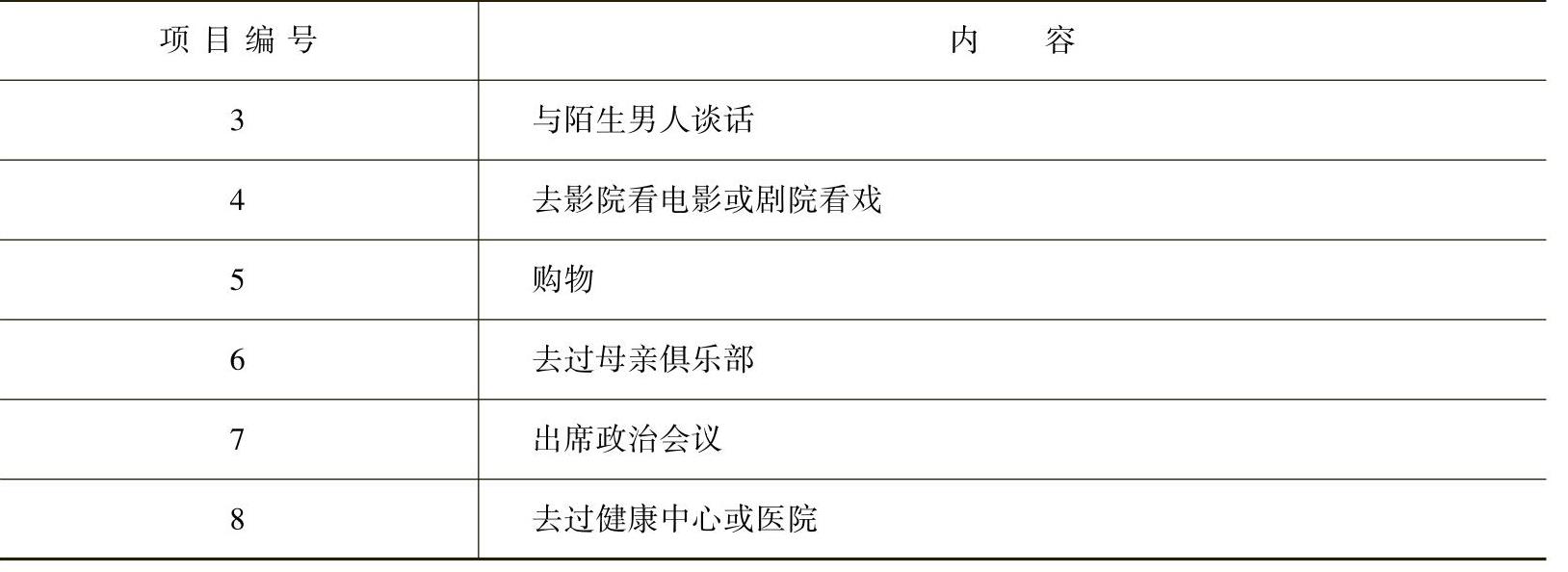
作为对孟加拉国妇女生育率定期调查的一部分,Huq和Cleland收集了社会自由流动性数据。他们对8445名农村妇女是否可以单独从事某些活动进行了问卷调查(见表6.1)。
表6.1 妇女的社会自由流动性所使用的变量

(续)
【例6.2】使用这个示例数据构建自编码网络。
(1)加载依赖的包和数据
>require(RcppDL)
>require("ltm")
>data(Mobility)
>data<=Mobility
(2)数据准备
从8445个样本中不重复抽取了1000个样本观测值。其中800个观测值用作训练集,剩下200个观测值用作测试集。
>set.seed(17)
>n=nrow(data)
>sample<=sample(1:n,1000,FALSE)
>data<=as.matrix(Mobility[sample,])
>n=nrow(data)
>train<=sample(1:n,800,FALSE)创建训练样本和测试样本代码如下:
>x_train<=matrix(as.numeric(unlist(data[train,])),nrow=nrow(data[train,]))
>x_test<=matrix(as.numeric(unlist(data[-train,])),nrow=nrow(data[-train,]))
需要进行检查以确保有正确的样本容量。训练集应该为800个观测值,测试集应该有200个观测值。
>nrow(x_train)
[1]800
>nrow(x_test)
[1]200
所有这些看起来都还不错。现在把原来的响应变量从属性R对象中删除。在这个例子中,将Item3(与一个不了解的男人说话)作为响应变量。下面代码示例怎样将Item3从属性对象中删除:
>x_train<=x_train[,-3]
>x_test<=x_test[,-3]
(3)建模
接下来使用RcppDL包中的Rsda函数构造降噪自编码网络。需要用两个响应变量。首先为训练样本创建响应变量。
>y_train<=data[train,3]
>temp<=ifelse(y_train==0,1,0)
>y_train<=cbind(y_train,temp)
对于测试样本,遵循相同的程序。
>y_test<=data[-train,3]
>temp1<=ifelse(y_test==0,1,0)
>y_test<=cbind(y_test,temp1)
现在来详细说明模型。以上构造了一个没有任何噪声的堆栈自编码网络,两个隐藏层,每层包含10个结点。
>hidden=c(10,10)
>fit<=Rsda(x_train,y_train,hidden)(https://www.xing528.com)
Rsda默认的噪声等级是30%。因为是从一个常规的堆栈自编码网络开始的,所以将噪声设置为0。
>setCorruptionLevel(fit,x=0.0)
注意:可以在Rsda包中设置很多参数。
>setCorruptionLevel(model,x)也可以为微调和预训练阶段选择样本数量和学习率。
setFinetuneEpochs
setFinetuneLearningRate
setPretrainLearningRate
setPretrainEpochs
预训练和微调模型相当简单。
>pretrain(fit)
>finetune(fit)
(4)模型部署
因为样本很小,所以模型收敛很快。可以使用测试样本来看看对响应变量预测的概率。
>predProb<=predict(fit,x_test)
>head(predProb,6)
[,1] [,2]
[1,] 0.4481689 0.5518311
[2,] 0.4481689 0.5518311
[3,] 0.4481689 0.5518311
[4,] 0.6124651 0.3875349
[5,] 0.4481689 0.5518311
[6,] 0.8310412 0.1689588
观察到模型预测的前三个观测值中有45%属于1类,55%属于2类。来看看它是怎样实现的。
>head(y_test,3)

虽然第一个观测错过了!然而,第二个和第三个观测值正在被正确地分类。最后,构建混淆矩阵。
>pred1<=ifelse(predProb[,1]>=0.5,1,0)
>table(pred1,y_test[,1],dnn=c("Predicted","Observed"))
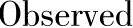

接下来,重建模型。这一次添加25%的噪声。
>setCorruptionLevel(fit,x=0.25)
>pretrain(fit)
>finetune(fit)
>predProb<=predict(fit,x_test)
>pred1<=ifelse(predProb[,1]>=0.5,1,0)
>table(pred1,y_test[,1],dnn=c("Predicted","Observed"))
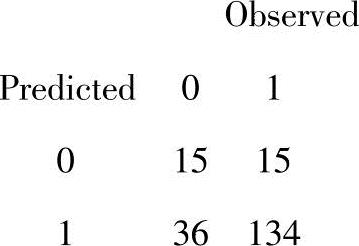
这个混合矩阵与没有任何噪声的堆栈自编码网络的一样。所以,在这种情况下添加噪声没有多少好处。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




