【例5.1】建立一个SAE模型,压缩R-LOG图像并提取隐含特征。
(1)加载依赖的包和数据
>require(autoencoder)
>require(ripa)
autoencoder包包含需要的函数来建立稀疏自编码网络。Ripa包包含一个R-LOG图像,加载图像如图5.6所示。
>data(logo)
图5.6 图像R-LOG
查看图像的特征:
>logo
size:77×101
type:grey
这是一个灰度大小77×101像素的图像。
(2)建模
首先,复制这张图像并赋值给x_train。用t()转置图像来使得它适合autoencoder包的使用。
>x_train<-t(logo)
x_train是101行(样本),77列(属性)的灰度图像。
现在使用autoencoder函数建立SAE模型。
>set.seed(2016)
>fit<-autoencode(X.train=x_train,X.test=NULL,
nl=3,N.hidden=60,
unit.type="logistic",
lambda=1e-5,
beta=1e-5,
rho=0.3,
epsilon=0.1,
max.iterations=100,
optim.method=c("BFGS"),
rel.tol=0.01,
rescale.flag=TRUE,
rescaling.offset=0.001)
第二行表示模型将保存在R对象fit;并将x_train里的图像数据传输到函数中。参数n1代表层数被设置为3。使用逻辑激活函数,隐藏结点数目为60。lambda是一个权重衰减参数,通常设置为一个较小的值;beta有着相同的值,它是稀疏性惩罚项的权重。稀疏度设置为0.3(rho)并按正态分布N(0,epsilon2)采样。iterations的最大值设置为100。注意:rescale.flag=true统一重新调节训练矩阵x_train,因此它的值位于0~1之间(logistic激活函数)。
查看fit相关的属性:
attributes(fit)
$names
[1]"W" "b"
[3]"unit.type" "rescaling"
[5]"nl" "sl"
[7]"N.input" "N.hidden"
[9]"mean.error.training.set" "mean.error.test.set"
$class
[1]"autoencoder"下面代码`查看训练集均值误差:
>fit$mean.error.training.set
[1]0.3489713
(3)模型预测
正如看到的,SAE经常对提取隐藏结点的特征是有用的。使用hidden.output=TRUE实现预测。
>features<-predict(fit,X.input=x_train,hidden.output=TRUE)
由于隐藏结点的数目设置为60,属性的数目为77,特征是原始图像的紧凑表示,可视化表示为图5.7所示。
>image(t(features$X.output))
转置函数t()用于重新定位特征来匹配图5.7。
图5.7 从fit提取隐藏结点的特征
注意,使用Nelder-Mead、准线性牛顿(Quasi-Newton)法和共轭梯度算法的Autoencoder函数在数据包中被称为优化函数。目前的优化方法包括:
1)“BFGS”是一种拟牛顿方法,它使用函数值和梯度来建立一个图像表面进行优化。
2)“CG”是一个共轭梯度算法,通常比BFGS方法更脆弱。它的主要优点是运行时不需要存储大量的矩阵。
3)“L-BFGS-B”允许每个变量被给一个较低或者较高的限制。
压缩特征如何捕获原始图像?使用hidden.out=FALSE的预测函数来重建值。
>pred<-predict(fit,X.input=x_train,hidden.output=FALSE)均方误差显得相当小。
>pred$mean.error
[1]0.3503714(https://www.xing528.com)
重建图像(见图5.8),表明用SAE表示原始图像相当得好!
>recon<-pred$X.output
>image(t(recon))
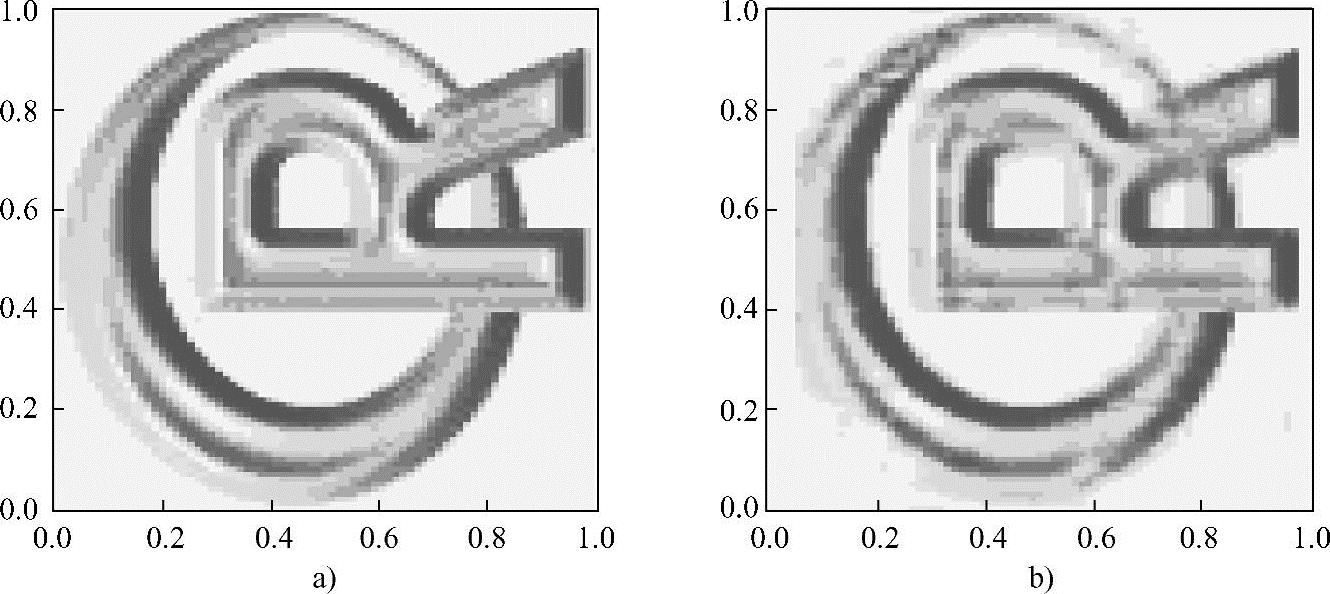
图5.8 原始标志和稀疏Autoencoder重建标志
a)原始标志 b)稀疏Autoencoder重建标志
【例5.2】用SAE和R执行一个可使用的软体动物分析。
通过本例的学习,思考如何把使用的方法来适应自己的研究。
鲍鱼、海洋蜗牛、蛤、扇贝、海参、章鱼和鱿鱼都属于一类海洋生物(软体动物)。本例使用来自UCI机器学习档案的鲍鱼数据集来预测鲍鱼的年龄(通过壳上环数),给定大量的属性,例如外壳尺寸(高度、长度、宽度)和重量(壳重、去壳重量、脏器重量、整个重量)。下面代码是如何使用R链接到数据集:
>aburl="http://archive.ics.uci.edu/ml/machine-learning-databases/abalo ne/abalone.data"
使用read.table加载数据并存储到R对象data。
>names=c("sex","length","diameter","height","whole.weight",
"shucked.weight","viscera.weight",
"shell.weight","rings")
>data=read.table(aburl,header=F,sep=",",col.names=names)
使用summary函数来考查不寻常的观测数据。
>summary(data)
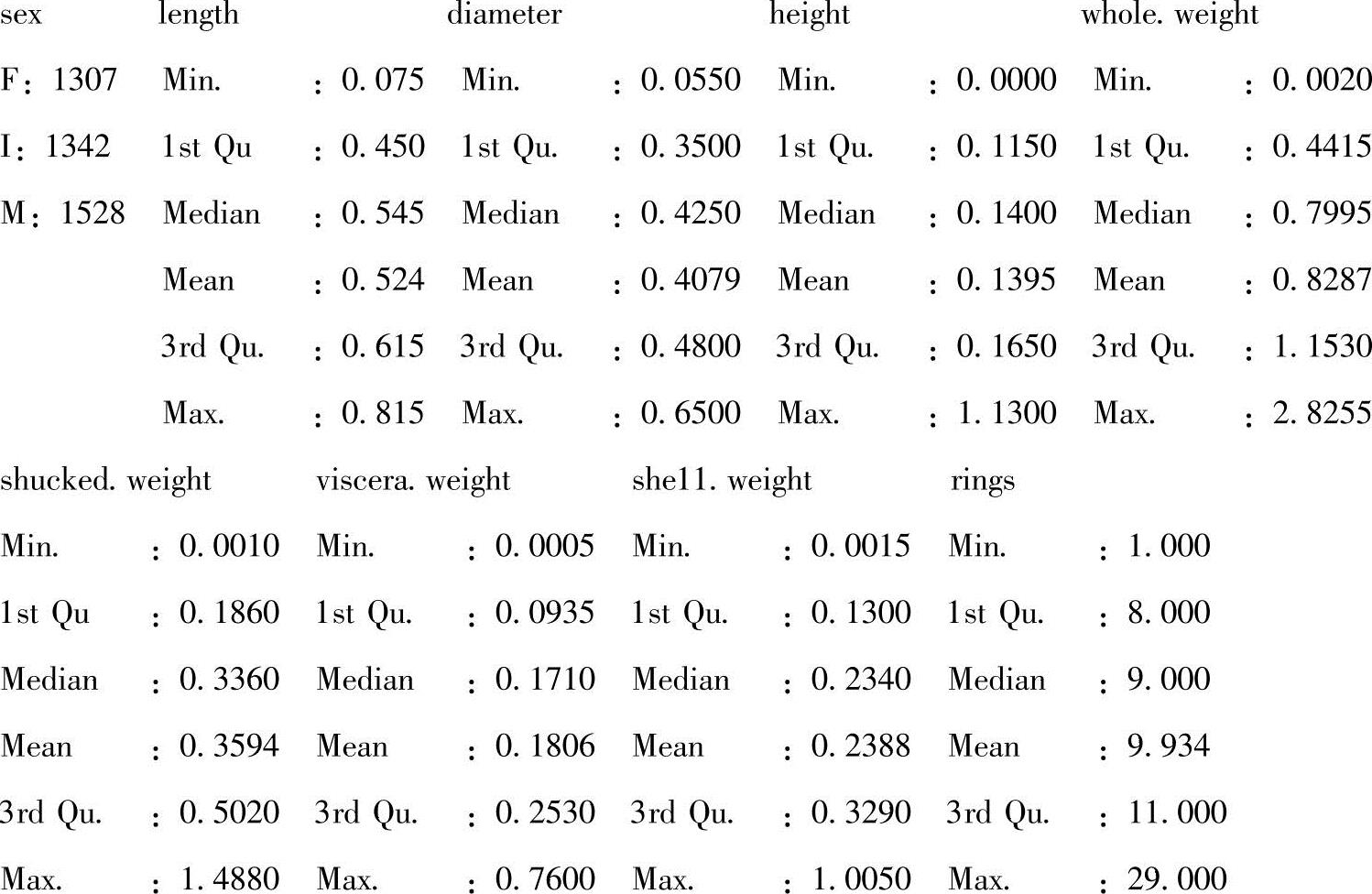
可以看出,鲍鱼高度存在问题;一些蜗牛高度为0,这是不可能的。进一步考查:
>data[data$height==0,]
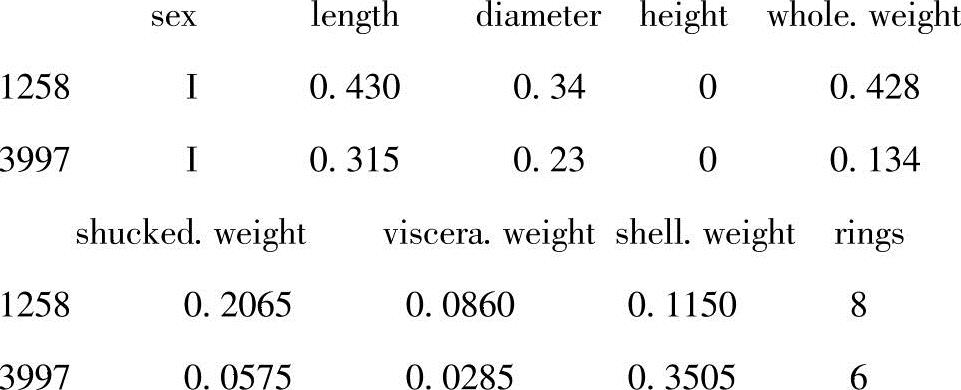
显现出了两个蜗牛高度为0的观测数据(样本编号为1258和3997)。需要删除这些观测样本。
>data$height[data$height==0]=NA
>data<-na.omit(data)
>data$sex<-NULL #去掉性别列
>summary(data)
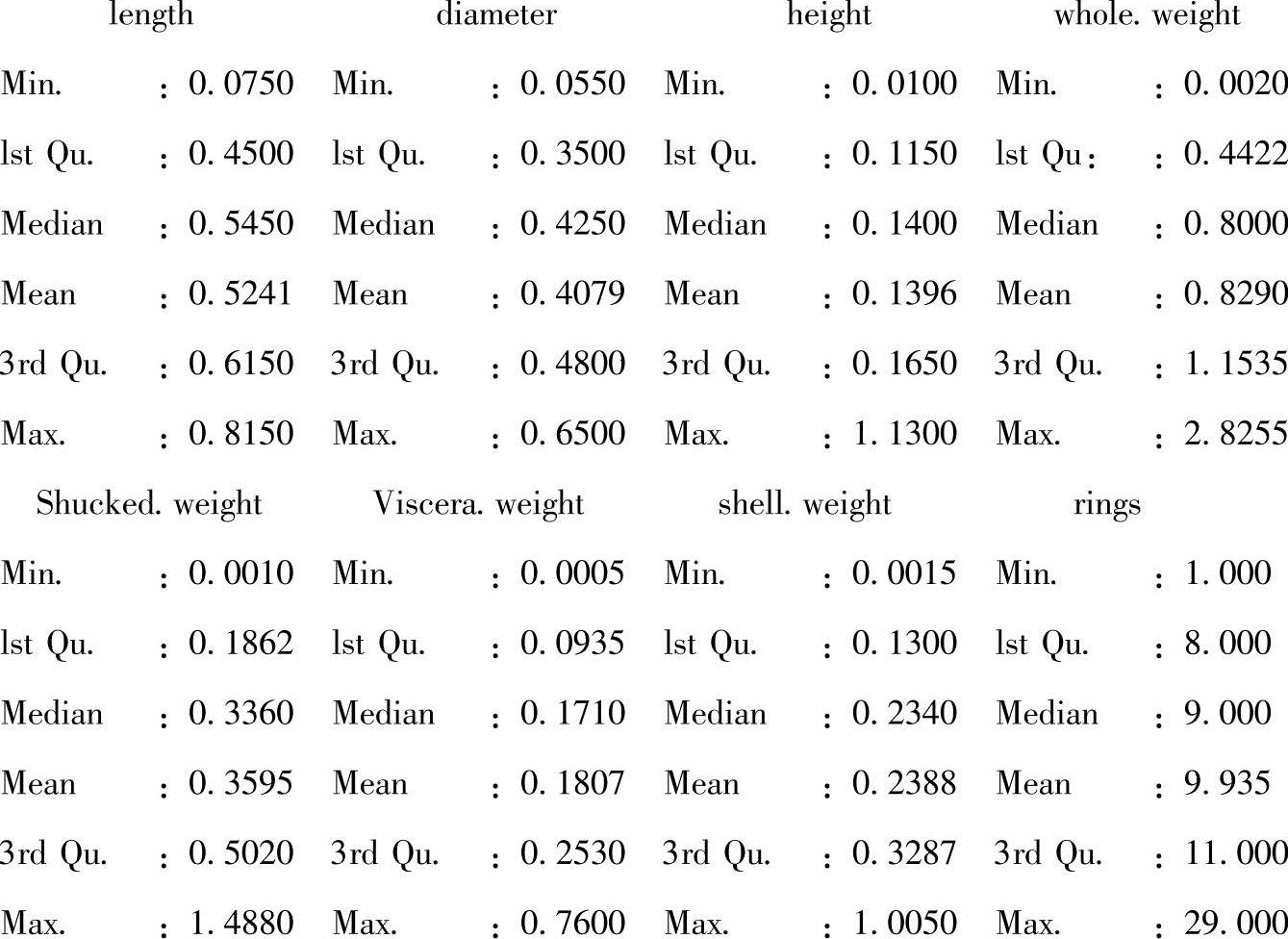
似乎数据都是合理的。接下来,转换数据,将它转换为一个矩阵,并将结果存储于R对象data1。

lambda=1e-5,
beta=1e-5,
rho=0.07,
epsilon=0.1,
max.iterations=100,
optim.method=c("BFGS"),
rel.tol=0.01,
rescale.flag=TRUE,
rescaling.offset=0.001)
注意:有5个隐藏结点的模型和一个稀疏参数为7%。一旦模型被优化,均方误差小于2%。
>fit$mean.error.training.set
[1]0.01654644
通过设置hidden.output=TRUE。由于隐藏结点的数目少于特征数目,feature$X.output输出降维数据:
>features<-predict(fit,X.input=data1[,train],hidden.output=TRUE)
>features$X.output

使用predict函数重构并存储结果到R对象pred。
>pred<-predict(fit,X.input=data1[,train],hidden.output=FALSE)
图5.9、图5.10和图5.11使用雷达图可视化重建的值。
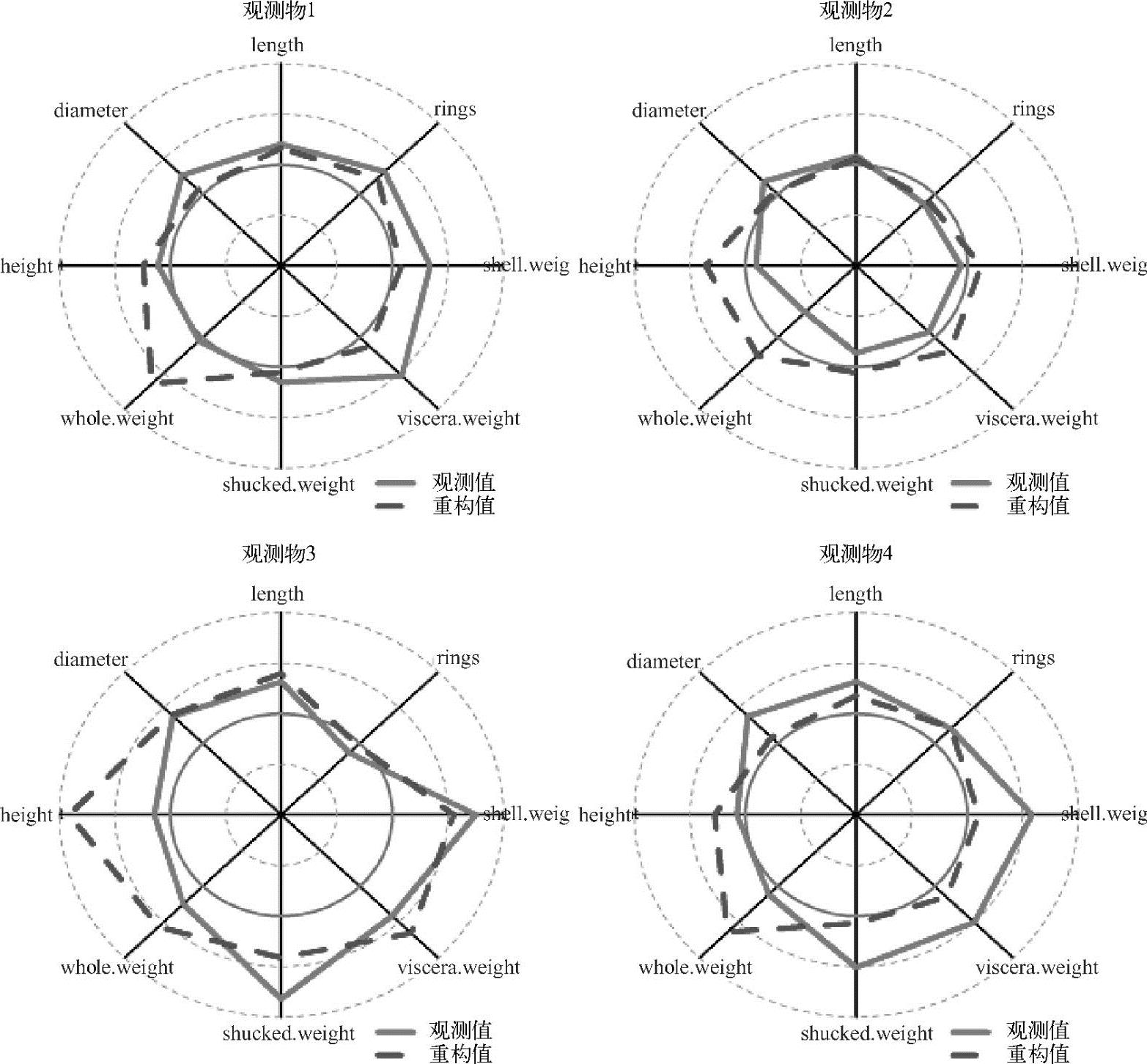
图5.9 对于观测物1~4所观测和重构的值
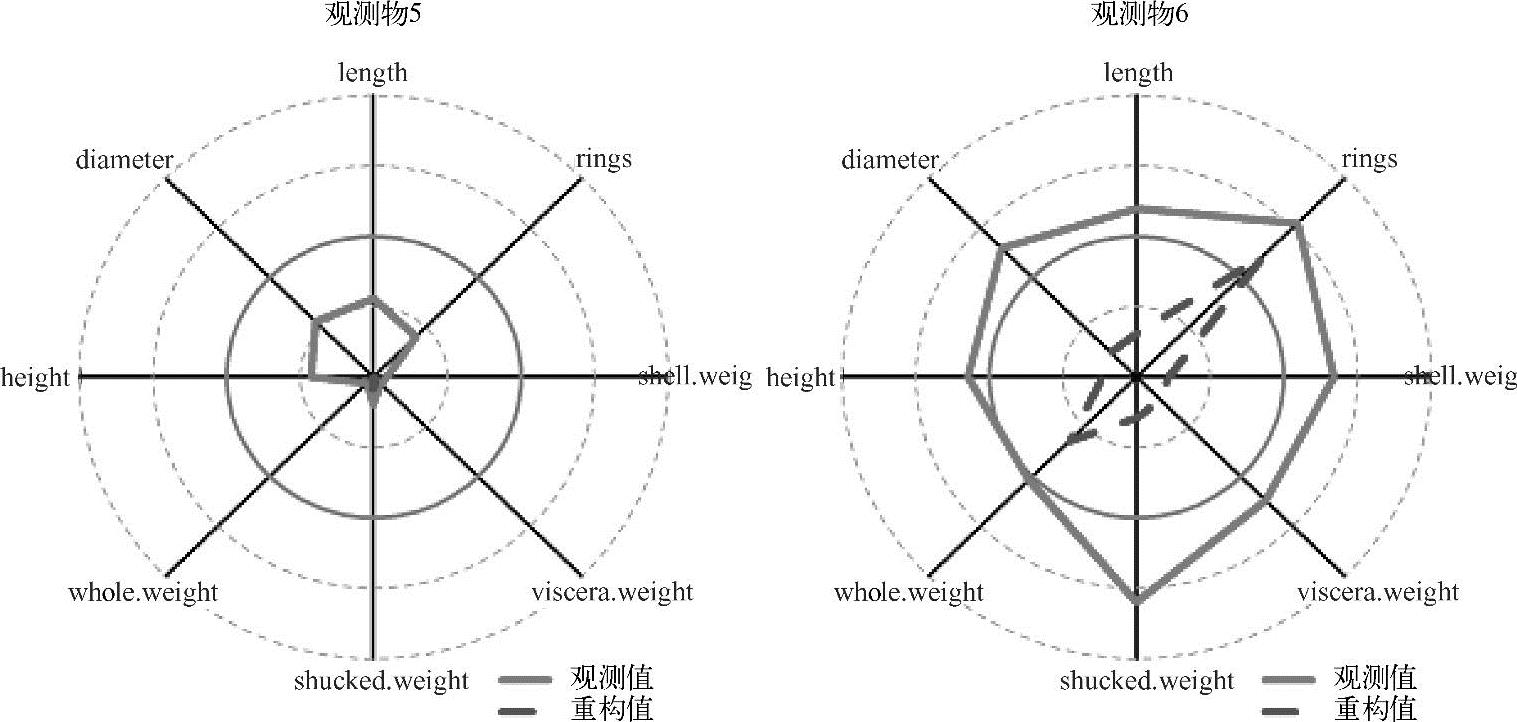
图5.10 观测物5~8所观测和重构的值
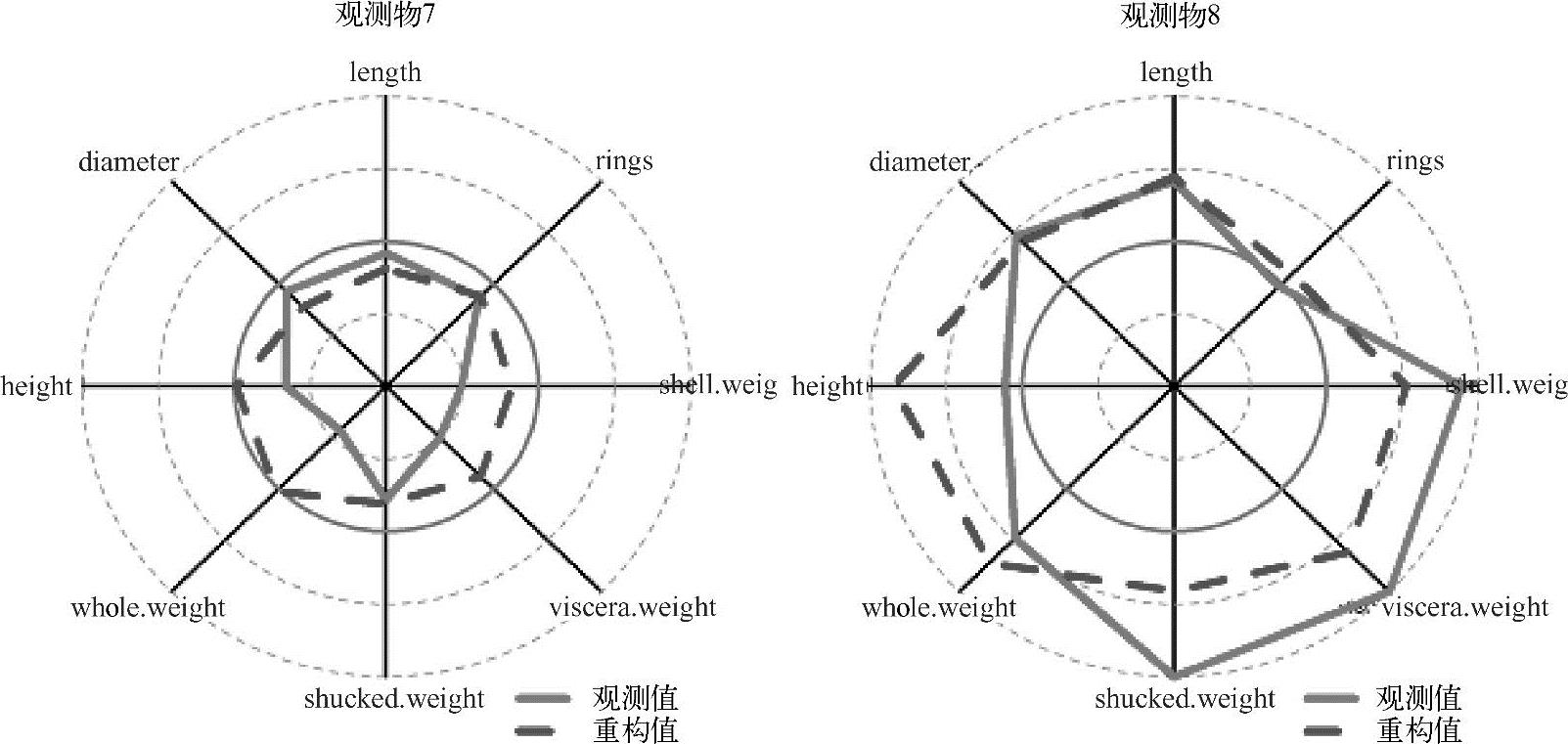
图5.10 观测物5~8所观测和重构的值(续)
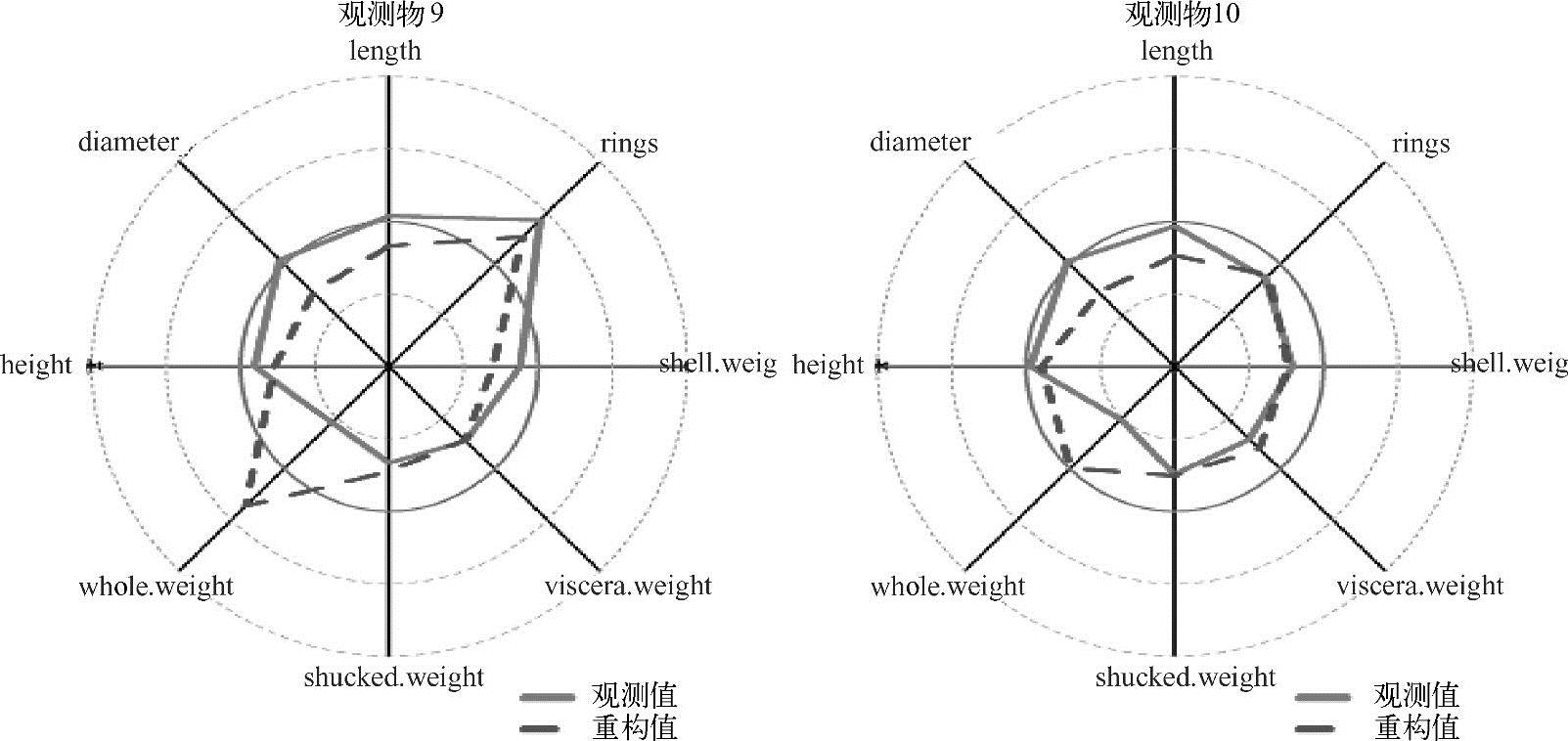
图5.11 观测物9~10所观测和重构的值
整体重建的值提供了一个原始值的合理表达。注意,观测样本5拟合程度不如样本6;进一步考查图5.12所示的柱状图,图中显示了重建值和观测值之间的差异。重建值在所有八个维度(属性)under-fit观测值。在观测样本5最明显的是环,重建环的值为1.4,相对所观测到的值为3.5。观测样本6观测到一个类似的模式。
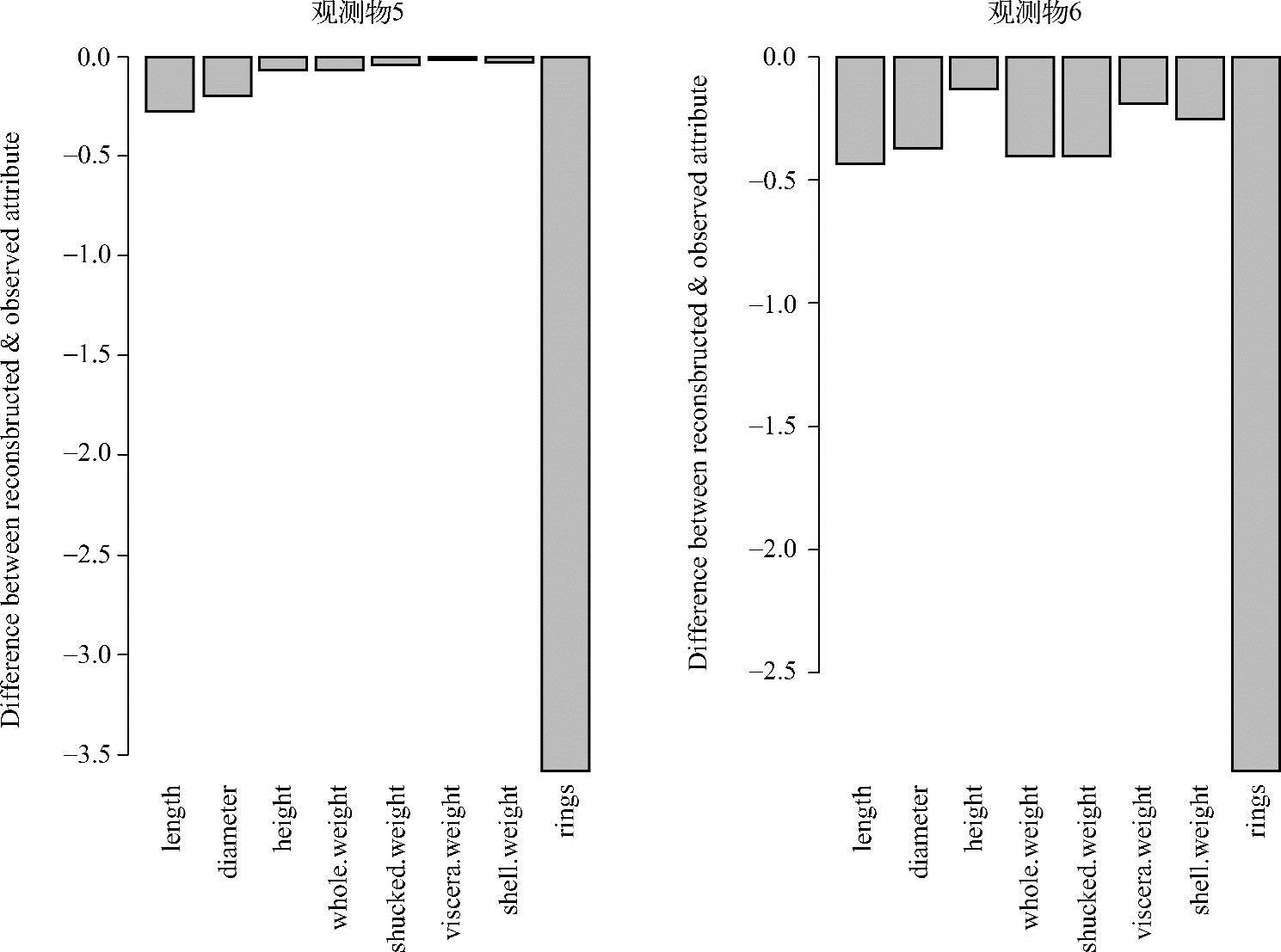
图5.12 观测物5、6的柱状图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




