【摘要】:自编码网络是一种无监督学习三层前向反馈神经网络,架构如图5.4所示,与多层感知器非常相似,它包括一个输入层、隐藏层和输出层。AE由编码器和译码器组成。举个例子,在图5.4中,AE使用三个隐藏单元,每一个单元包含sigmoid激活函数h1、h2、h3,将属性x1、x2、x3、x4、x5、x6编码,解码后得到x^i(i=1,…AE可以学习到数据的一些压缩(降维)表示,即输入数据的另一种相关性表示。
自编码网络(AE)是一种无监督学习三层前向反馈神经网络,架构如图5.4所示,与多层感知器非常相似,它包括一个输入层、隐藏层和输出层。输入层的神经元数目和输出层的神经元数目是相同的。隐藏层神经元的数目少于或者多于输入神经元的数目。它不同于MLP,因为输出层有着和输入层一样多的结点,而不是通过给出的x来训练预测一些目标值y。
AE由编码器和译码器组成。输入层到隐藏层的映射被称为编码器;隐藏层到输出层的映射被称为解码器。编码器采用输入属性的向量,通常通过在隐藏层的sig-moid激活函数将它们转化为新的特征,然后解码器将这些特征转换回原来的输入属性。举个例子,在图5.4中,AE使用三个隐藏单元,每一个单元包含sigmoid激活函数h1、h2、h3,将属性x1、x2、x3、x4、x5、x6编码,解码后得到x^i(i=1,…,6)的原始属性的估计。
AE尝试学习一个hw,b(x)≈x的函数,也就是说,使得输出x^接近于输入x。为了使这个函数有意义,需要加入一些限制条件(比如限制隐藏层神经元的数目,即稀疏性)。AE可以学习到数据的一些压缩(降维)表示,即输入数据的另一种相关性表示。
稀疏性限制是指如果当神经元的输出接近于1的时候认为它被激活,而输出接近于0的时候认为它被抑制,那么使得神经元大部分的时间都是被抑制的限制则被称作稀疏性限制。这里假设神经元的激活函数是sigmoid函数。(https://www.xing528.com)
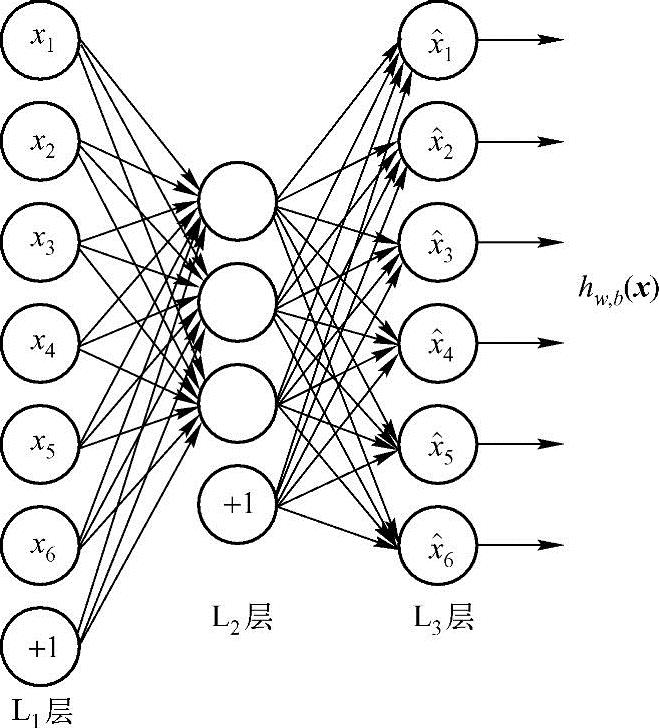
图5.4 基本AE结构
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




