使用R语言实现时序预测模型，预测英国支气管炎、肺气肿和哮喘死亡总人数

在英国，天气总是一个聊谈的话题，因为，英格兰的天气总是在变化。你可以在一天里体验四个季节。

【例4.1】使用Jordan网络建立诺丁汉市气温预测模型。

与Elman网络类似，Jordan网络模型也是对时间序列数据的建模工具。

（1）加载使用的包和数据

＞library（RSNNS）

＞library（quantmod）

＞library（datasets）

＞data（nottem）

数据是datasets包的nottem数据集，nottem数据集包含了诺丁汉市，每年每月平均测量空气温度。首先了解一下nottem的数据结构：

＞nottem

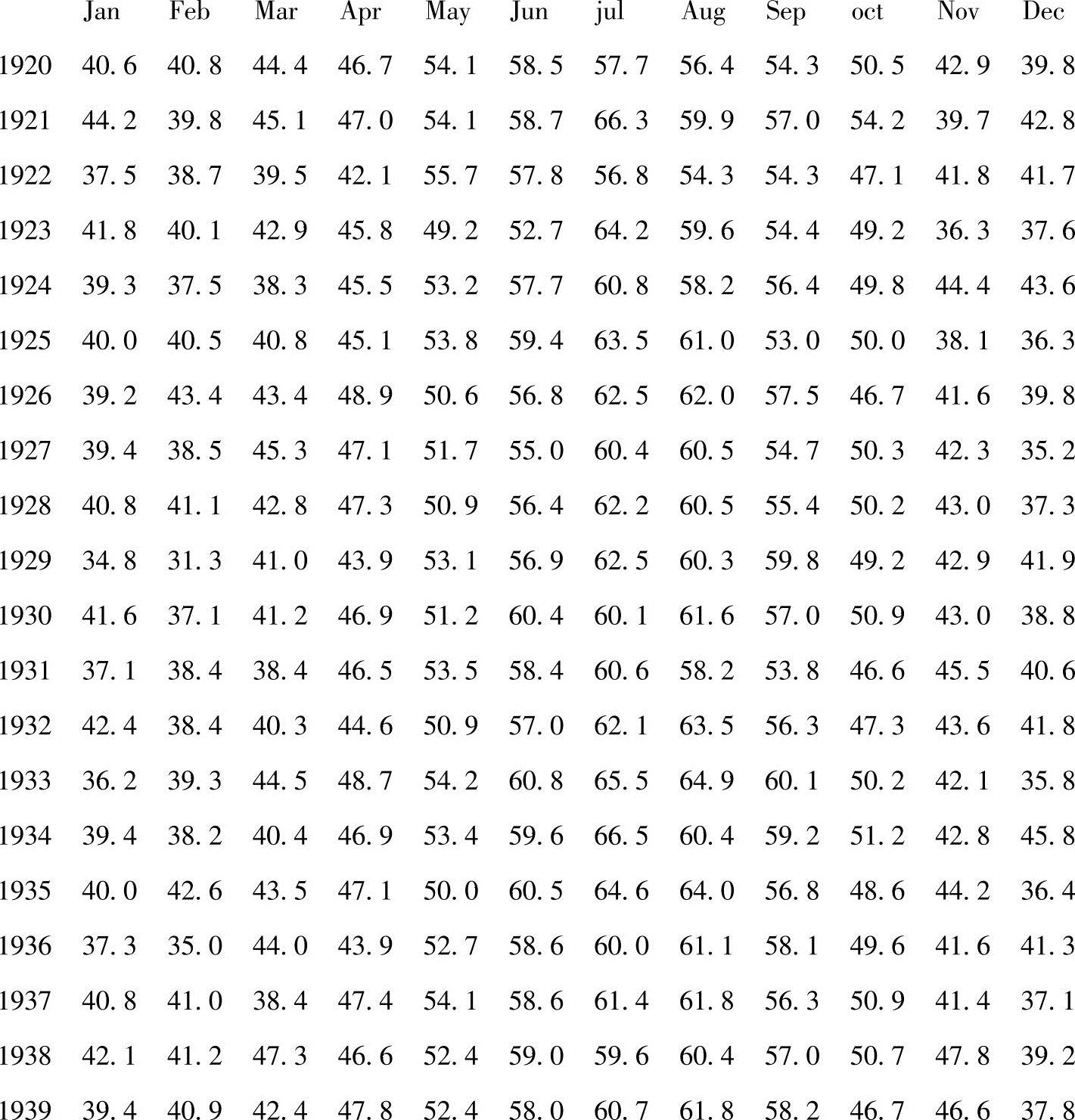
没有出现任何缺失值，检查一下nottem数据类型：

＞class（nottem）

[1]＂ts＂

Nottem是一个时间序列ts对象，了解数据的类型是非常重要的，特别是使用日期类型或R的不同类型的混合。

图4.6显示了nottem观察数据的时间序列散点图。数据覆盖1920～1939年，虽然没有任何明显趋势，然而它确实表现出强烈的季节性。

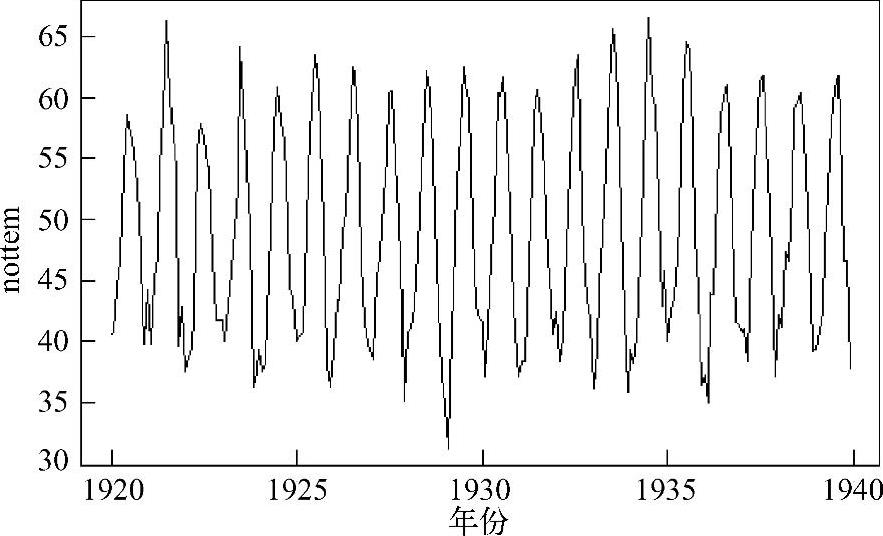
图4.6 1920～1939年诺丁汉市月平均温度

画时间序列散点图命令如下：

＞plot（nottem）

（2）数据探索

在使用神经网络模型之前，需要归一化数据的属性。下面给出常用的四种归一化方法：

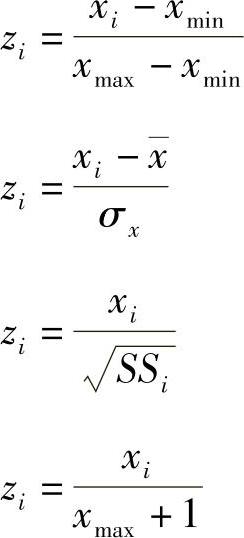
式中，SS_i是x_i的平方和；x^-是x_i的均值；σ_x是x_i的标准差。因为没有任何说明性变量，所以，首先使用log变换数据，再使用scale函数标准化数据。

＞y＜-as.ts（nottem）

＞y＜-log（y）

＞y＜-as.ts（scale（y））

因为建模数据有很强的季节性特征，似乎依赖于月，所以使用滞后12个月的数据作为Jordan网络12个属性的输入。Quantmod包的Lag函数需要的数据类型为zoo类。

＞y＜-as.zoo（y）

＞x1＜-Lag（y，k=1）

＞x2＜-Lag（y，k=2）

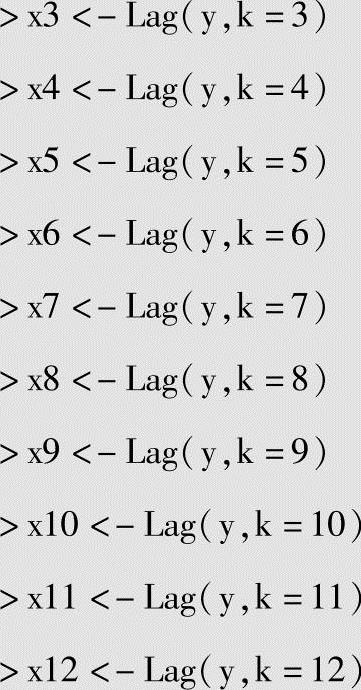
与Elman神经网络类似，需要删除NA值，最后将清洗后的数据存入temp中。

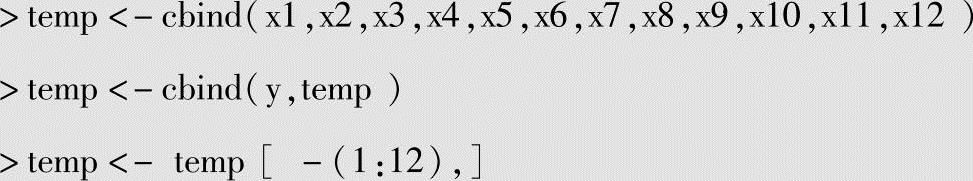
数据探索最后一步是使用plot函数可视化所有属性和响应变量的分布，如图4.7所示。

＞plot（temp）

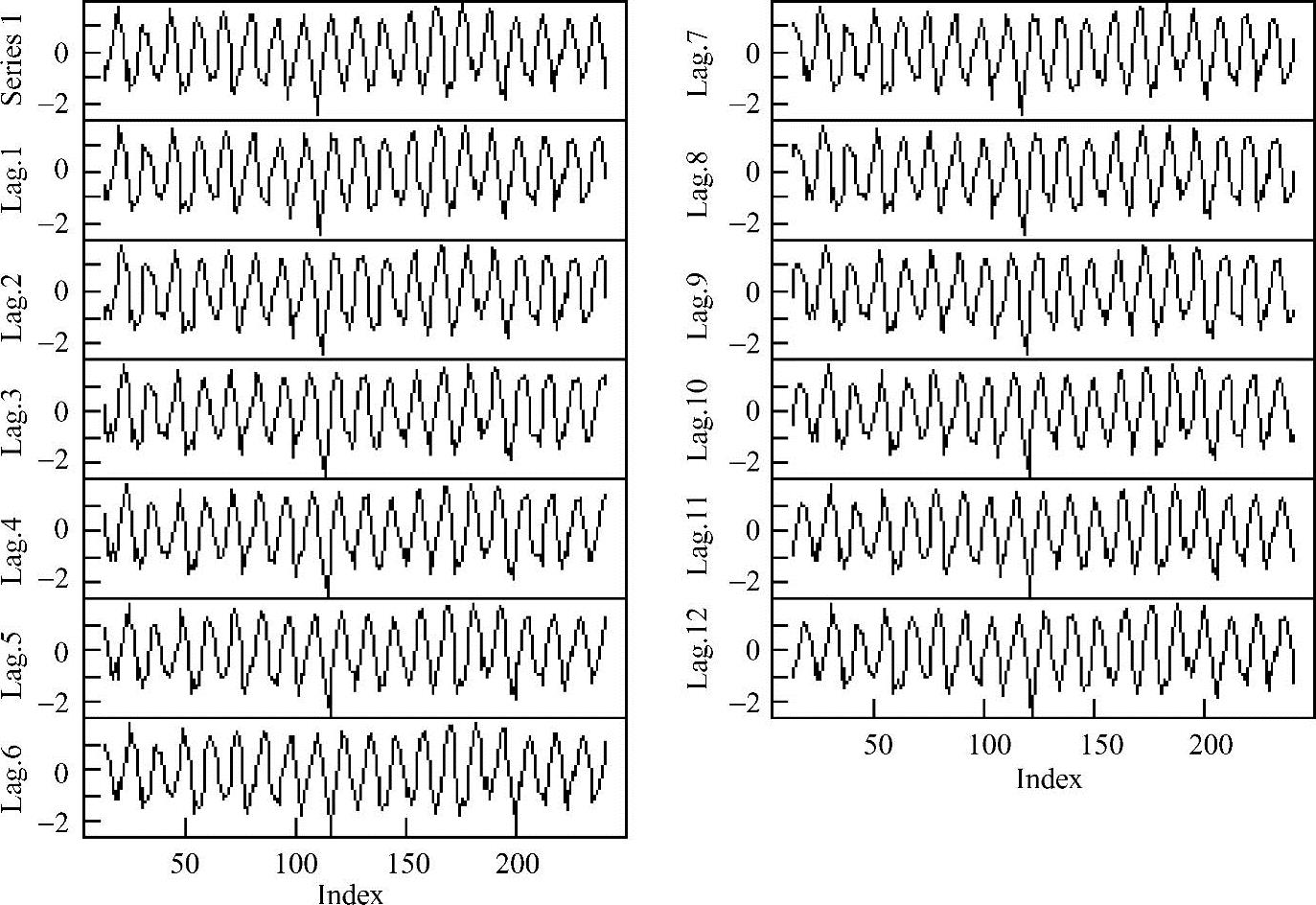
图4.7 Jordan网络响应变量和属性分布图

（3）训练样本选择

＞n=nrow（temp） #观测数据个数

＞n

[1]228

＞set.seed（465） #设置种子

＞n_train＜-190#设置训练集大小

＞train＜-sample（1：n，n_train，FALSE） #随机选取190个训练样本

（4）建模

＞inputs＜-temp[，2：13] #属性变量

＞outputs＜-temp[，1] #响应变量

＞fit＜-jordan（inputs[train]，outputs[train]，#建模

size=2， #隐藏层数

learnFuncParams=c（0.01）， #学习率

maxit=1000） #最大迭代次数

（5）模型部署

使用plotIterativeError函数显示迭代误差，如图4.8所示。

＞plotIterativeError（fit）

前100次迭代误差下降相当快，大约迭代300次趋于稳定。

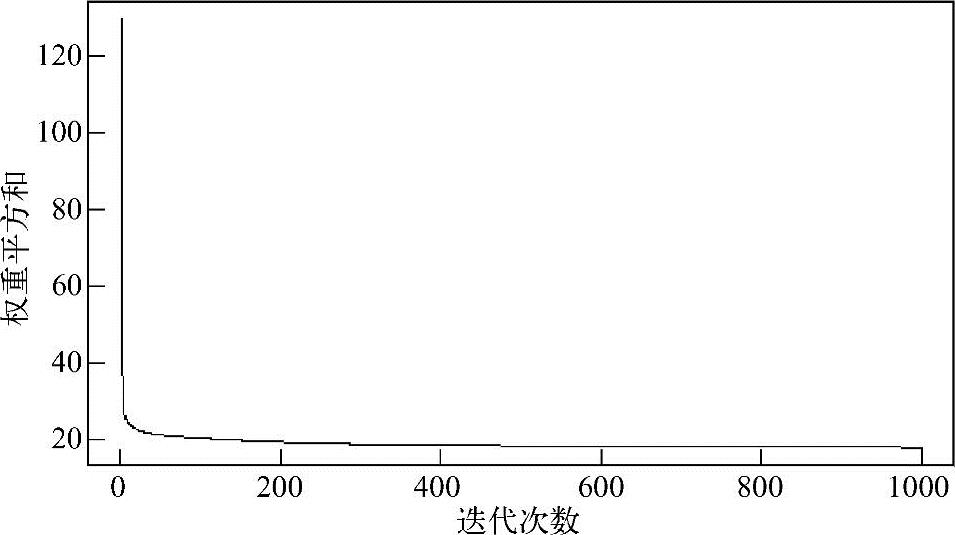
图4.8 训练误差与迭代次数

使用predict函数对测试样本进行预测，并计算测试样本响应变量和预测值之间的平方相关系数。

＞pred＜-predict（fit，inputs[-train]）

＞cor（outputs[-train]，pred）^2

[1，]0.9050079

因为平方相关系数大于0.9，所以模型是成功的。

【例4.2】建立一个RNN模型，预测在英国死于支气管炎、肺气肿、哮喘的总人数。

（1）检查机器上安装了哪些包

＞pack＜-as.data.frame（installed.packages（）[，c（1，3：4）]）

＞rownames（pack）＜-NULL

＞pack＜-pack[is.na（pack$Priority），1：2，drop=FALSE]

＞print（pack，row.names=FALSE）

（2）加载需要的包和数据

＞library（RSNNS）

＞library（quantmod）

＞library（datasets）

＞data（UKLungDeaths）

使用的数据在datasets包里面，所需要的数据结构为UKLungDeaths。dataests包是默认加载的包，所以不需要专门加载它。但是，调用它也是一种有益的练习。

UKLungDeaths数据库包含了3个1974～1979年英国每个月支气管炎、肺气肿、哮喘的死亡人数的时间序列。第一个时间序列是死亡的总人数（ldeaths）；第二个时间序列是男性死亡人数（mdeaths）；第三个时间序列是女性死亡人数（fmdeaths）。可以通过使用plot函数可视化这些数据（见图4.9），方法如下：

＞par（mfrow=c（1，3）） #窗口划分为1行3列

＞plot（ldeaths，xlab=＂Year＂，ylab=＂Both sexes＂，main=＂Total＂）

＞plot（mdeaths，xlab=＂Year＂，ylab=＂Males＂，main=＂Males＂）

＞plot（fdeaths，xlab=＂Year＂，ylab=＂Females＂，main=＂Females＂）

总而言之，随着时间的推移，可以看到死亡人数有着巨大的变化，每月死亡人数的波动清晰可见。可以观察到，1976年出现每月最高和最低的死亡总数。有趣的是，对于男性来说，每个周期的最低点呈现下降的趋势。而进入1979年以后所有的趋势都呈相当明显的下降。

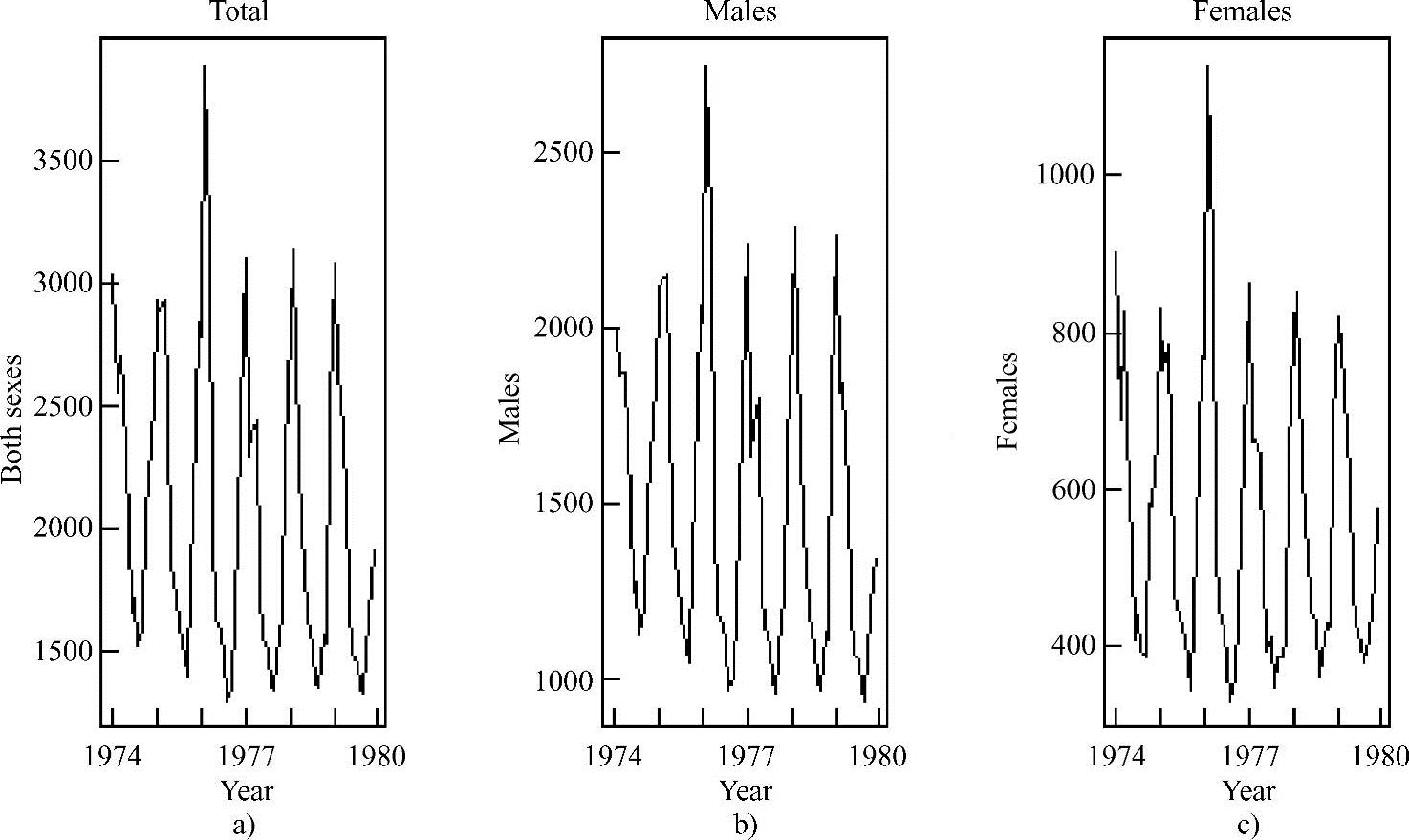
图4.9 英国每个月支气管炎、肺气肿、哮喘死亡人数

a）总人数 b）男性死亡人数；c）女性死亡人数(www.xing528.com)

（3）数据探索

因为对死亡总数的建模感兴趣，所以重点分析ldeaths数据结构。在此之前，快速检查缺失数据。

＞sum（is.na（ldeaths））

[1]0

表示数据集ldeaths没有缺失数据，接下来，检查ldeaths类型。

＞class（ldeaths）

[1]＂ts＂

表示ldeaths是一个时间序列对象，图4.10显示了时间序列图、核密度图和箱线图。

＞par（mfrow=c（3，1）） #窗口划分为3行1列

＞plot（ldeaths）

＞x＜-density（ldeaths）

＞plot（x，main=＂UK total deaths from lung diseases＂）

＞polygon（x，col=＂green＂，border=＂black＂）

＞boxplot（ldeaths，col=＂cyan＂，ylab=＂NumbeR of deaths per month＂）

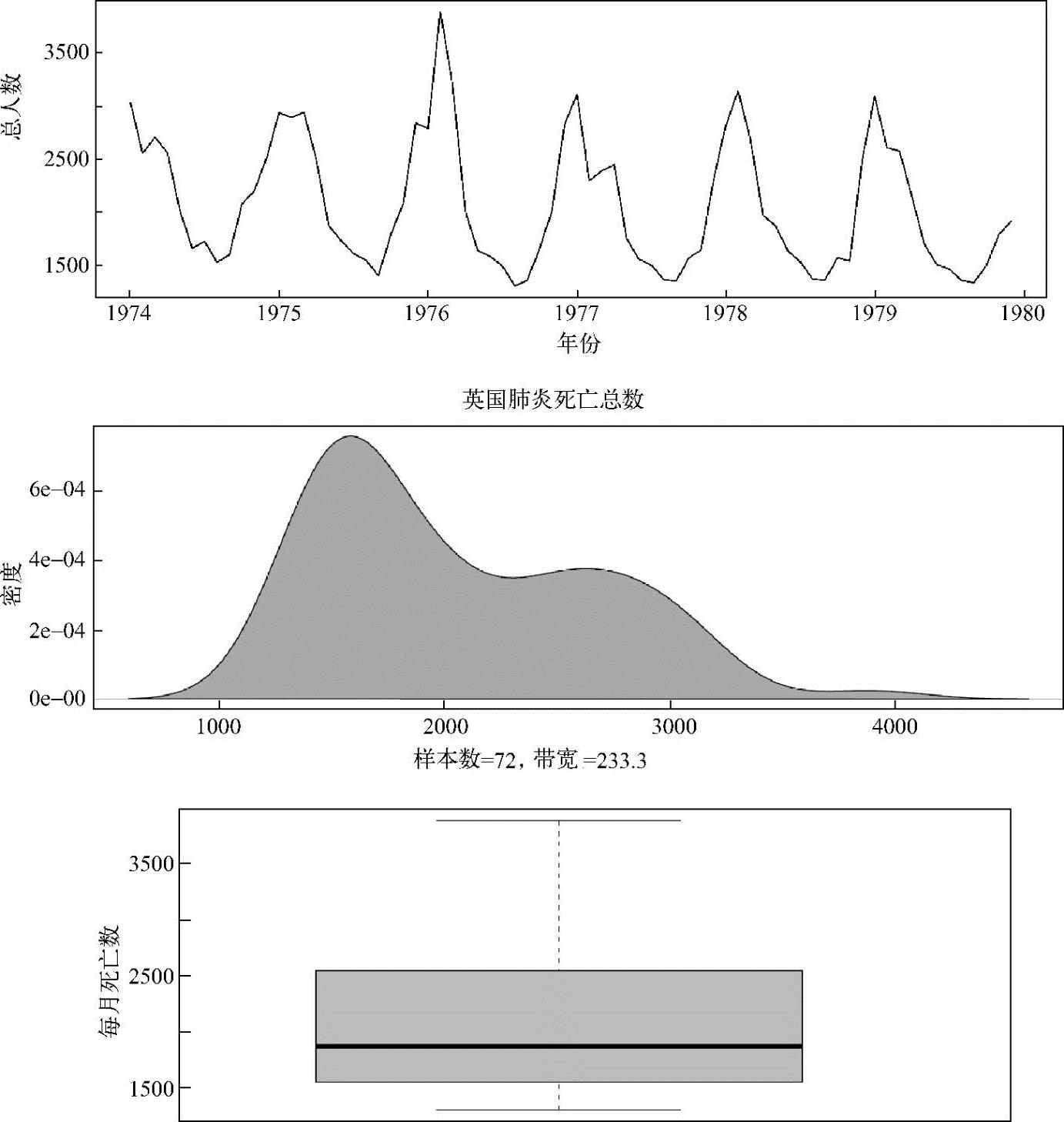
图4.10 死亡总数的形象化总结

（4）数据转换

由于数据似乎存在某种规律，所以将其转换成一种适合进行Elman神经网络工作的形式。首先，将数据复制一份，存储在变量y中。

＞y＜-as.ts（ldeaths）

当使用时间序列时，一般将数据转换成对数。将数据转换成对数，数据会更加规范化。

＞y＜-log（y）

通过scale函数使数据看起来更加规范。

＞y＜-as.ts（scale（y））

注意，as.ts函数确保变换后仍然是ts对象。

既然无法将这个数据归于其他的类别，那么就使用纯时间序列的方法。这种建模方法的主要问题是需要多少滞后变量（lags）？既然是对一年内的每个月都进行了观察，所以使用12作为滞后变量。实现这个操作的方法是使用quantmod包里面的Lag操作函数，这就需要将y转变成一个zoo类的对象。

＞y＜-as.zoo（y）

x1＜-Lag（y，k=1）

x2＜-Lag（y，k=2）

x3＜-Lag（y，k=3）

x4＜-Lag（y，k=4）

x5＜-Lag（y，k=5）

x6＜-Lag（y，k=6）

x7＜-Lag（y，k=7）

x8＜-Lag（y，k=8）

x9＜-Lag（y，k=9）

x10＜-Lag（y，k=10）

x11＜-Lag（y，k=11）

x12＜-Lag（y，k=12）

通过这个操作得到了12个属性作为神经网络的输入。下一步是将这12个观测值组合成一个数据框。

＞deaths＜-cbind（x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11，x12）＞deaths＜-cbind（y，deaths）观察deaths里面包含什么。

＞head（round（deaths，2），10）

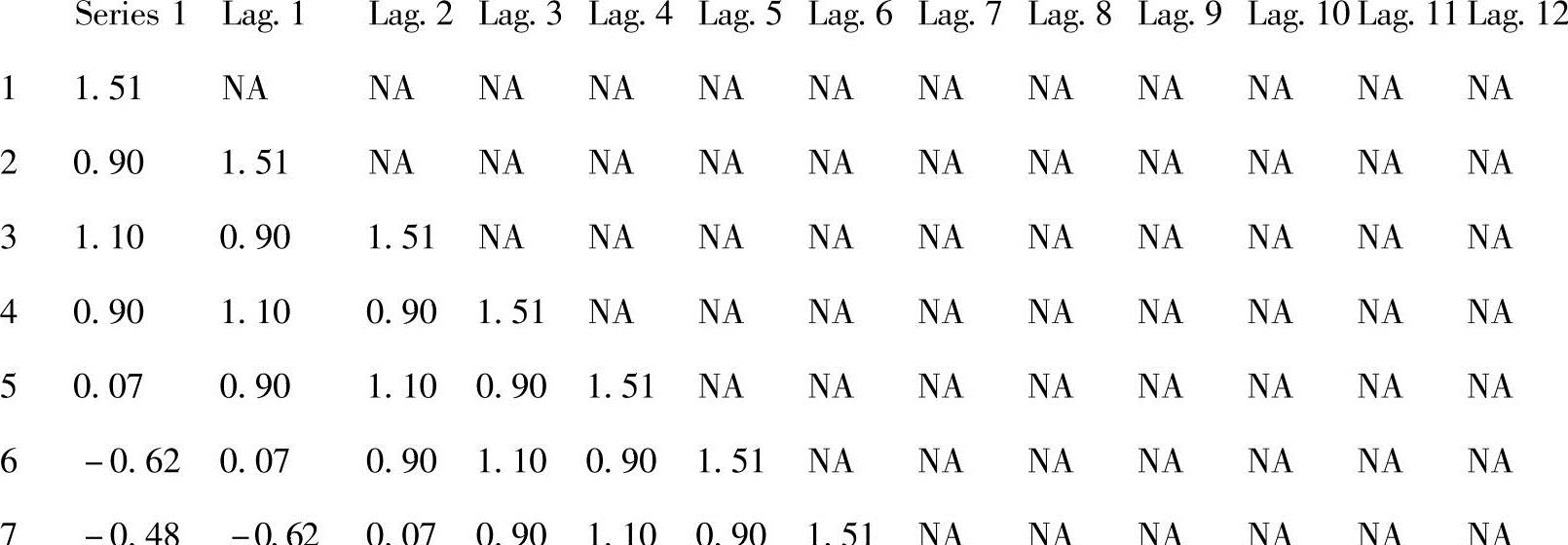
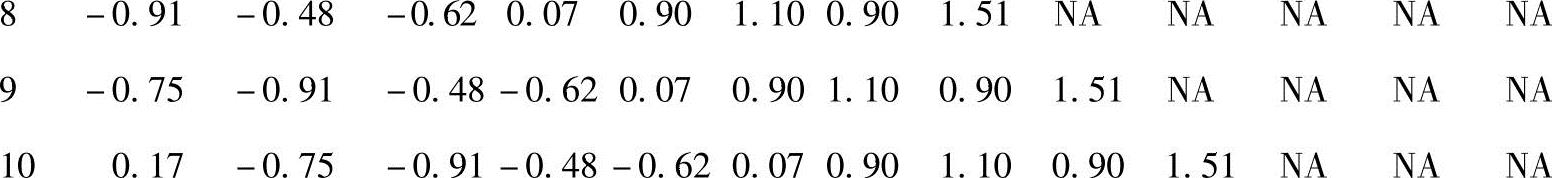
注意到NA的滞后值从1增大到12。使用延迟的目的就是为了得到这个结果。然而，需要从数据集里面删去NA观测值。

＞deaths＜-deaths[-（1：12），]

现在已经准备好开始创建训练集和测试集。首先，计算出数据的行数，并且使用set.seed函数来输出它。

＞n=nrow（deaths）

＞n

[1]60

＞set.seed（465）

作为一种快速的检测方法，可以看到有60行的观测数据可以用来作为分析。为了解决滞后值的问题，删除了12行的观测值，而结果也达到了预期。

使用其中的45行数据来建模，剩下的15行用来作为测试集。用如下代码随机选择一些不重复的数据：

＞n_train＜-45

＞train＜-sample（1：n，n_train，FALSE）

（5）建模

为了使过程变得更加简单一点，可以将包含有滞后值的协方差的属性放入到R的inputs对象里面，将相应变量放到ouputs对象里面。

＞inputs＜-deaths[，2：13]

＞outputs＜-deaths[，1]

在每个神经网络中，配置有两个隐藏层，每个隐藏层里面都包含一个结点。并将学习速率设置为0.1，最大的迭代次数设置为1000。

＞fit＜-elman（inputs[train]，outputs[train]，size=c（1，1），

leaRnFuncPaRams=c（0.1），maxit=1000）

若给定一个较小的数据，模型的收敛会变得很快，可以画出如图4.11所示的误差函数。

＞plotIterativeError（fit）

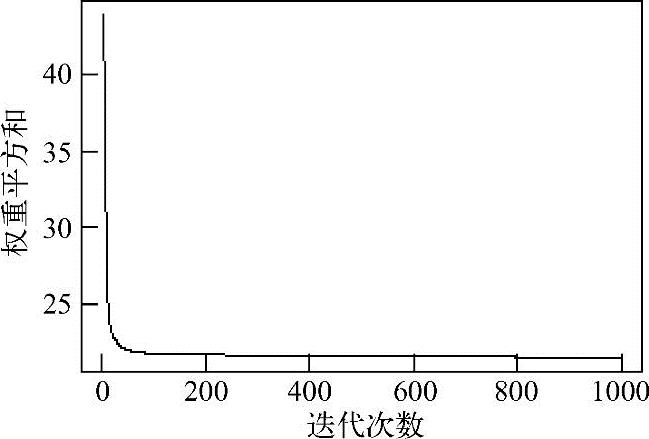
图4.11 Elman函数误差图像

从图4.11可以看出，误差迅速减小，大约在500次迭代后趋于稳定，可以使用summaRy函数来得到神经网络细节方面的信息。

＞summary（fit）通过这个函数可以得到很多R的输出值，找到输出中如下所示的部分。

unit definition seclion:

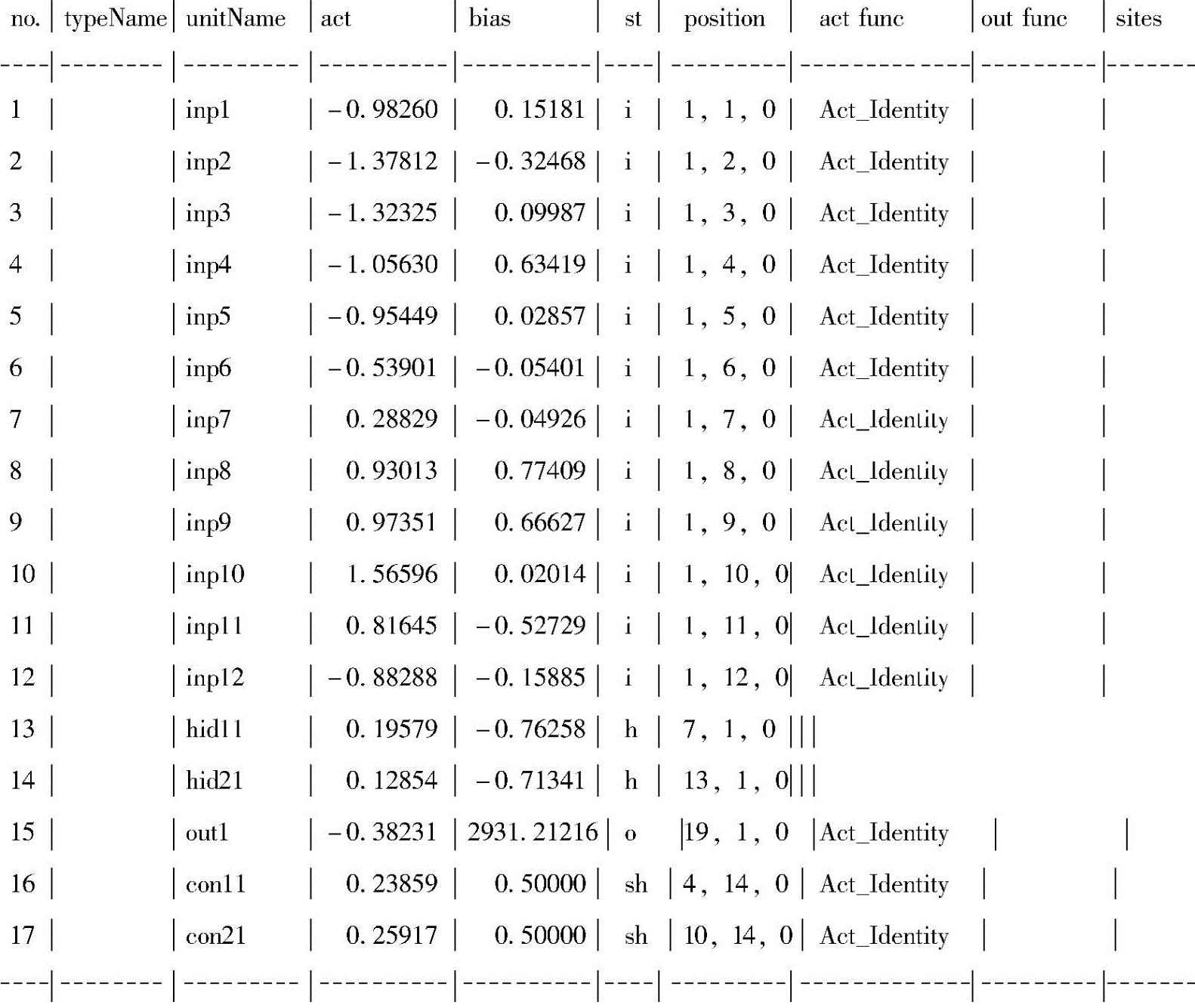
从第一列中，可以得到结点或者神经元的数量，而且可以知道这个网络一共有17行。它的第三列描述了神经元的类型，从中可以得知有12个输入神经元、2个隐藏神经元和1个输出神经元，在承接层有2个神经元。第四列和第五列给出了激活函数的值和每个神经元的偏置。例如，第一个神经元的激活函数值为-0.98260，偏置为0.15181。

（6）模型部署

现在，在测试集上用prRedict函数来测试一下这个模型。

＞pred＜-predict（fit，inputs[-train]）

＞plot（outputs[-train]，pred）

（7）模型评估

预测值和实际值的散点图如图4.12所示。

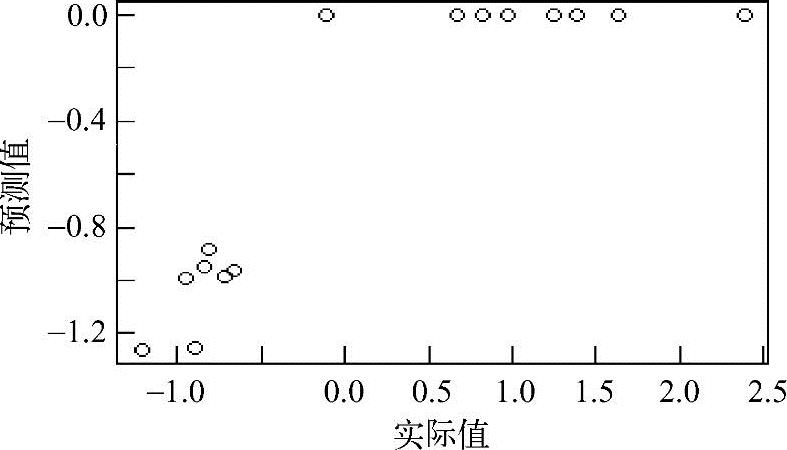
图4.12 RNN的实际值和预测值

＞cor（outputs[-train]，pred）^2

[，1]

[1，]0.7845

由此可知，平方相关系数为0.78。可以尝试不同的模型来提高这个系数，以达到理想值。试一试，通过重新建模来达到整体性能提高的效果。