实现多响应变量DNN模型的R代码

图像处理中，在单个DNN中通常要建立多个响应变量（像素）。然而，在数据科学领域，DNN模型通常只包含一个响应变量。

在同一组属性上建立多个响应变量联合模型的关键统计学原理是，它可以在回归类型模型中取得更有效的参数估计。简而言之，更有效的估计会得到更快的决策，因为这时在统计推断方面将会有更大的信心。可以想到多个涵盖商业、工业和研究的应用实例，其中在同一组属性上建立多个响应变量的模型是有用的。

【例2.3】使用TH.data包中的数据bodyfat来构建DNN。

该数据最初由Garcia等人收集，以通过测量皮肤厚度、周长以及男性和女性的骨宽度来开发用于体脂预测的可靠的回归方程。最初的研究收集了117名健康德国受试者的数据，其中有46名男性和71名女性。体脂数据包含71个女性的10个变量的数据，见表2.2。

表2.2 bodyfat数据集

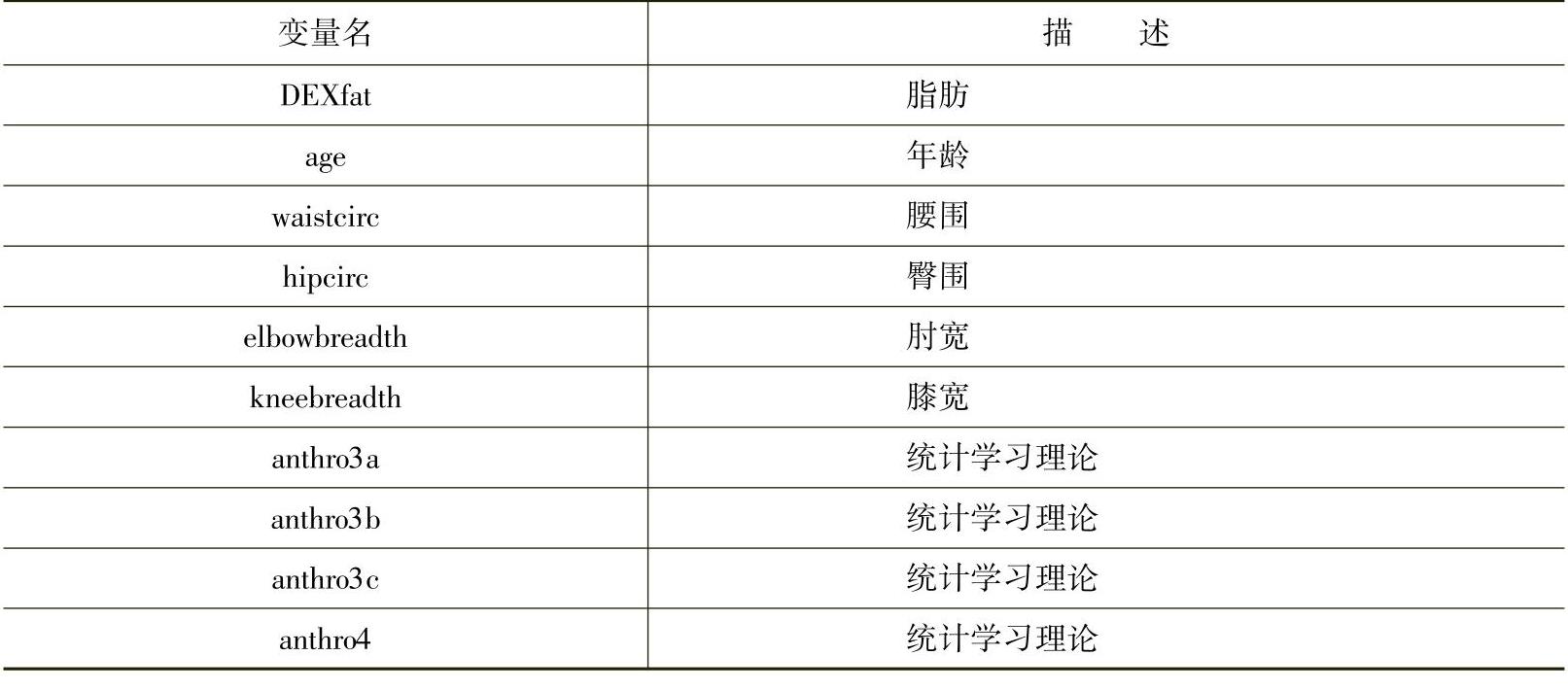
（1）加载使用的包和数据

＞library（neuralnet）

＞require（Metrics）

＞data（＂bodyfat＂，package=＂TH.data＂）

（2）数据准备

由于处理的是一个相当小的数据集，只有71个观测值，所以使用60个观测值作为训练样本。

＞set.seed（2016）

＞train＜-sample（1：71，60，FALSE） #构造训练集下一步，标准化观察值，用于构建DNN的公式存储在R对象f中：

＞scale_bodyfat＜-as.data.frame（scale（log（bodyfat）））

＞f＜-waistcirc+hipcirc～DEXfat+age+elbowbreadth+kneebreadth+anthro3a+anthro3b+anthro3c+anthro4

注意使用waistcirc+hipcirc～来表示两个响应变量。通常，对于k个响应变量{r₁，…，rk}，使用r₁+r₂+…+r_k～来表示。

（3）建模

使用两个隐藏层的模型来拟合，其中第一个隐藏层有8个神经元，第二个隐藏层有4个神经元。其余参数与已经讨论过的类似：

该模型只需要45步就会收敛，其平方误差的总和等于25.18。

然后，复制scale_bodyfat中的数据，并将赋值给without_fat，这样在scale_body-fat中保留一份原始值，稍后将会使用到它。注意，此时也需要使用NULL参数从这个新的R对象中删除响应变量：

＞without_fat＜-scale_bodyfat

＞without_fat$waistcirc＜-NULL

＞without_fat$hipcirc＜-NULL

（4）模型部署

现在把模型应用在测试样本上。第二行打印出预测值（仅显示前几个值）：

＞pred＜-compute（fit，without_fat[-train，]）

＞pred$net.result

[，1] [，2]

48 0.8324509945946 0.7117765670627

53 0.1464097674972 0.0389520756586

58 0.7197107887754 0.6215091479349

62 0.8886019185711 0.8420724129305

至此，具有两个响应变量的DNN已成功构建。

（5）模型评估

为了与线性回归模型做比较，需要建立两个模型。

模型1：

＞fw＜-waistcirc～DEXfat+age+elbowbreadth+kneebreadth+anthro3a+anthro3b+anthro3c+anthro4

＞fh＜-hipcirc～DEXfat+age+elbowbreadth+kneebreadth+anthro3a+anthro3b+anthro3c+anthro4

现在使用训练数据运行每个模型：

＞regw＜-linReg＜-lm（fw，data=scale_bodyfat[train，]）

＞regh＜-linReg＜-lm（fh，data=scale_bodyfat[train，]）

使用测试样本预测：

＞predw＜-predict（regw，without_fat[-train，]）

＞predh＜-predict（regh，without_fat[-train，]）

DNN模型与线性回归模型相比较，DNN模型响应变量的均方差统计量可以如下计算：

＞mse（scale_bodyfat[-train，10]，pred$net.result[，1]）

[1] 0.5376666652

Galton回归模型均方差：(www.xing528.com)

＞mse（scale_bodyfat[-train，10]，predw）

[1] 0.3670629158

Galton的腰围的线性回归模型优于深度学习模型。

臀部尺寸模型性能怎么样呢？以下是DNN的均方差度量：

＞mse（scale_bodyfat[-train，10]，pred$net.result[，2]）

[1] 0.5530302859

Galton的臀部尺寸回归模型的均方差度量：

＞mse（scale_bodyfat[-train，10]，predh）

0.5229634116

此时，两者速度较为接近，但线性回归模型仍然有较小的均方误差，性能略微优于DNN模型1。

模型2：

当然，在实践中，要使用不同的学习算法、不同的神经元数量来建立多种模型；线性回归模型结果仅作为一个有用的基准。为了说明这一点，使用deepnet包建立传统反向传播算法DNN。

首先，将属性变量赋值R对象X中，并将响应变量赋值R对象Y中：

＞set.seed（2016）

＞X=as.matrix（without_fat[train，]） #构造属性变量

＞Y=as.matrix（scale_bodyfat[train，3：4]） #构造响应变量

具有2个隐层的DNN模型如下：

＞fitB＜-nn.train（x=X，y=Y，

initW=NULL，

initB=NULL，

hidden=c（8，4），

activationfun=＂sigm＂，

learningrate=0.02，

momentum=0.74，

learningrate_scale=1，

output=＂linear＂，

numepochs=970，

batchsize=60，

hidden_dropout=0，

visible_dropout=0）

使用测试样本得到预测值，并存储在R对象predB中：

＞Xtest＜-as.matrix（without_fat[-train，]）

＞predB＜-nn.predict（fitB，Xtest）

腰围和臀围的均方误差计算过程如下：

＞mse（scale_bodyfat[-train，10]，predB[，1]）

[1] 0.1443659185

＞mse（scale_bodyfat[-train，10]，predB[，2]）

[1] 0.1409938484

依据均方误差，DNN模型2优于线性回归模型。

注：任何一种方法的优劣都不是绝对的，应该选择一种符合问题性质的方法。

腰围和臀围作为响应变量，可视化如图2.13所示。属性的可视化如图2.14所示。

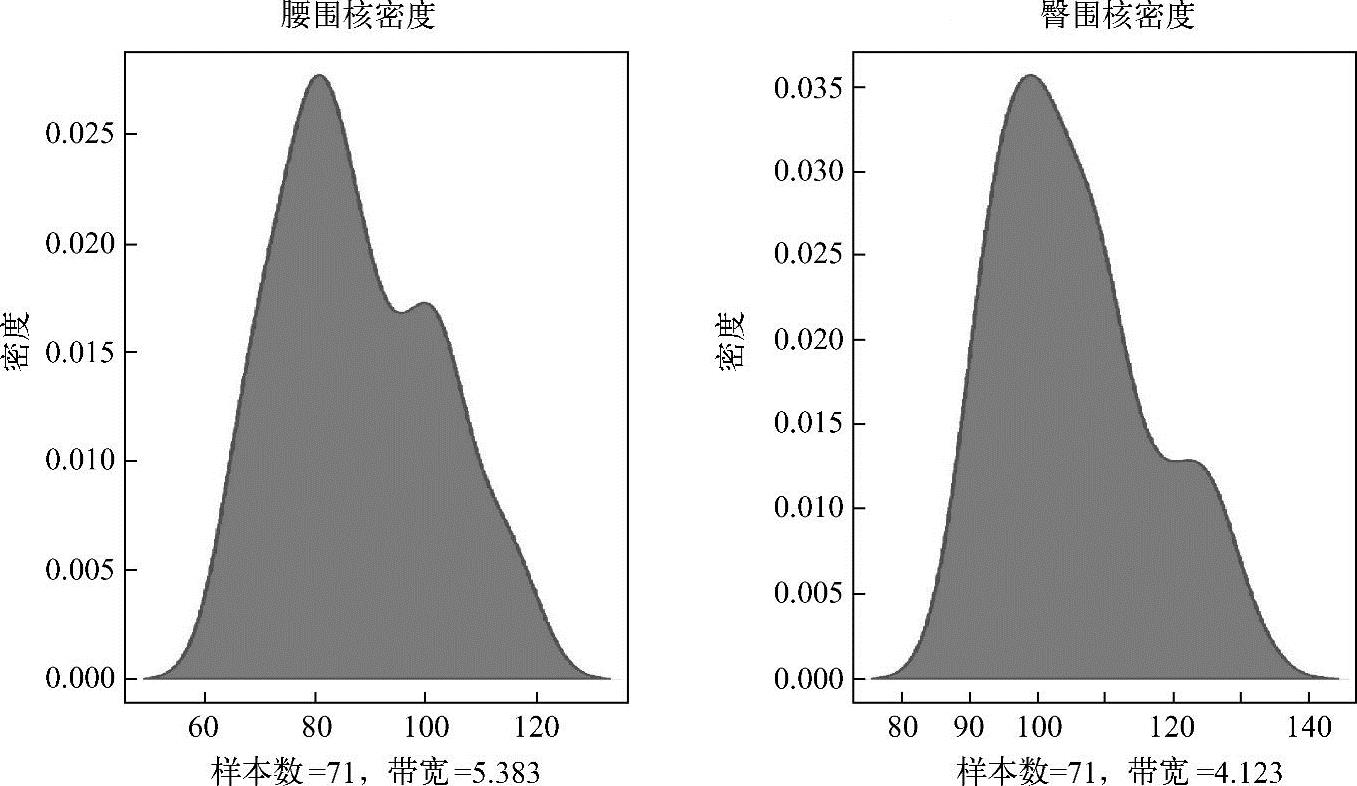
图2.13 响应变量分布图

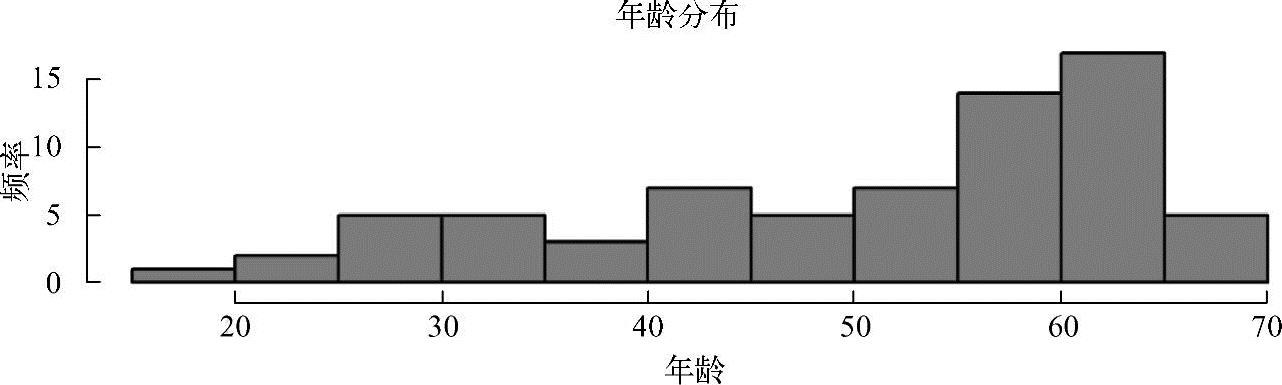
变量的提琴图

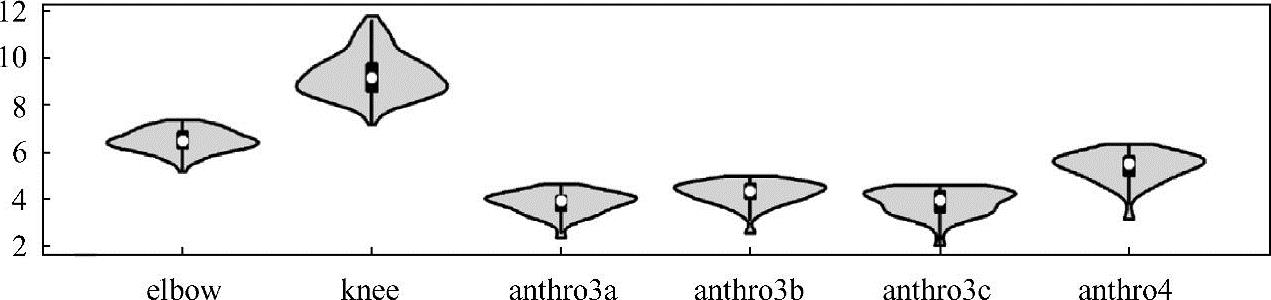
图2.14 DNN bodyfat属性

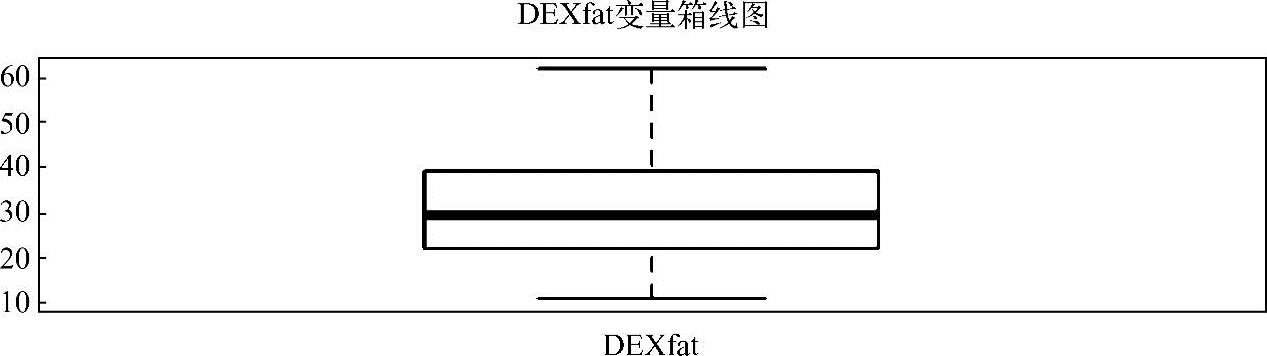
图2.14 DNN bodyfat属性（续）