（1）加载需要使用的包
＞library（neuralnet）
＞library（Metrics）
＞library（dplyr）
＞library（plyr）
数据集为MASS包中波士顿居民对空气质量改善付款意愿调查。
＞data（＂Boston＂，package=＂MASS＂）
＞data＜-Boston
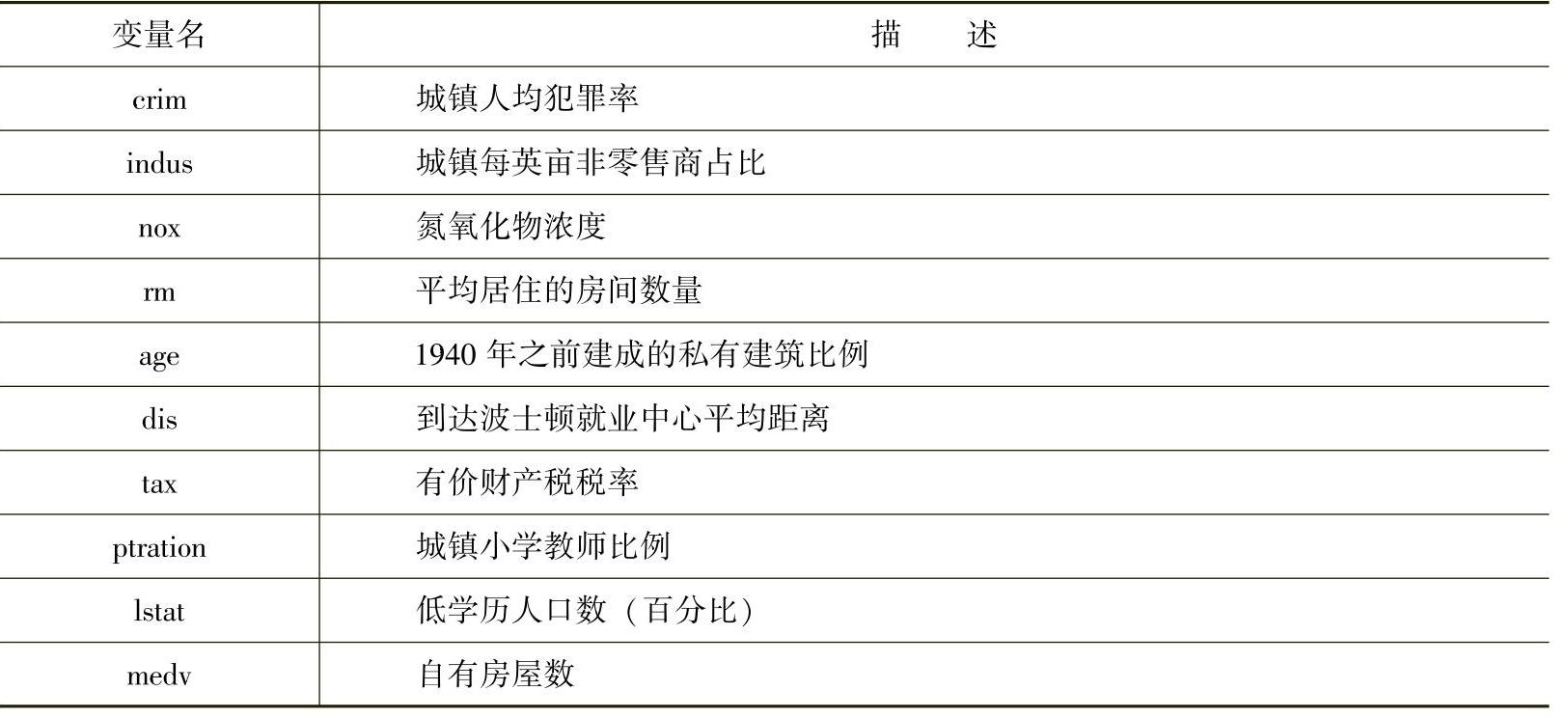
R对象Boston包含506行和14列，每列对应一个特定的变量。表2.1给出Bos-ton数据集每个变量的细节。
表2.1 Boston数据集
＞keeps＜-c（＂crim＂，＂indus＂，＂nox＂，＂rm＂，＂age＂，＂dis＂，＂tax＂，＂ptratio＂，＂lstat＂，
＂medv＂） #保留变量
＞data＜-data[keeps] #根据保留变量生成数据集
R对象data现在只包含接下来要使用的变量，响应变量为mdev。接下来，使用apply方法来快速查看一下保留的数据中是否有缺失值。
＞apply（data，2，function（x）sum（is.na（x）））
crim indus nox rm age dis taxptratio lstat medv
0 0 0 0 0 0 0 0 0 0
可以看出，没有缺失值！
执行代码：
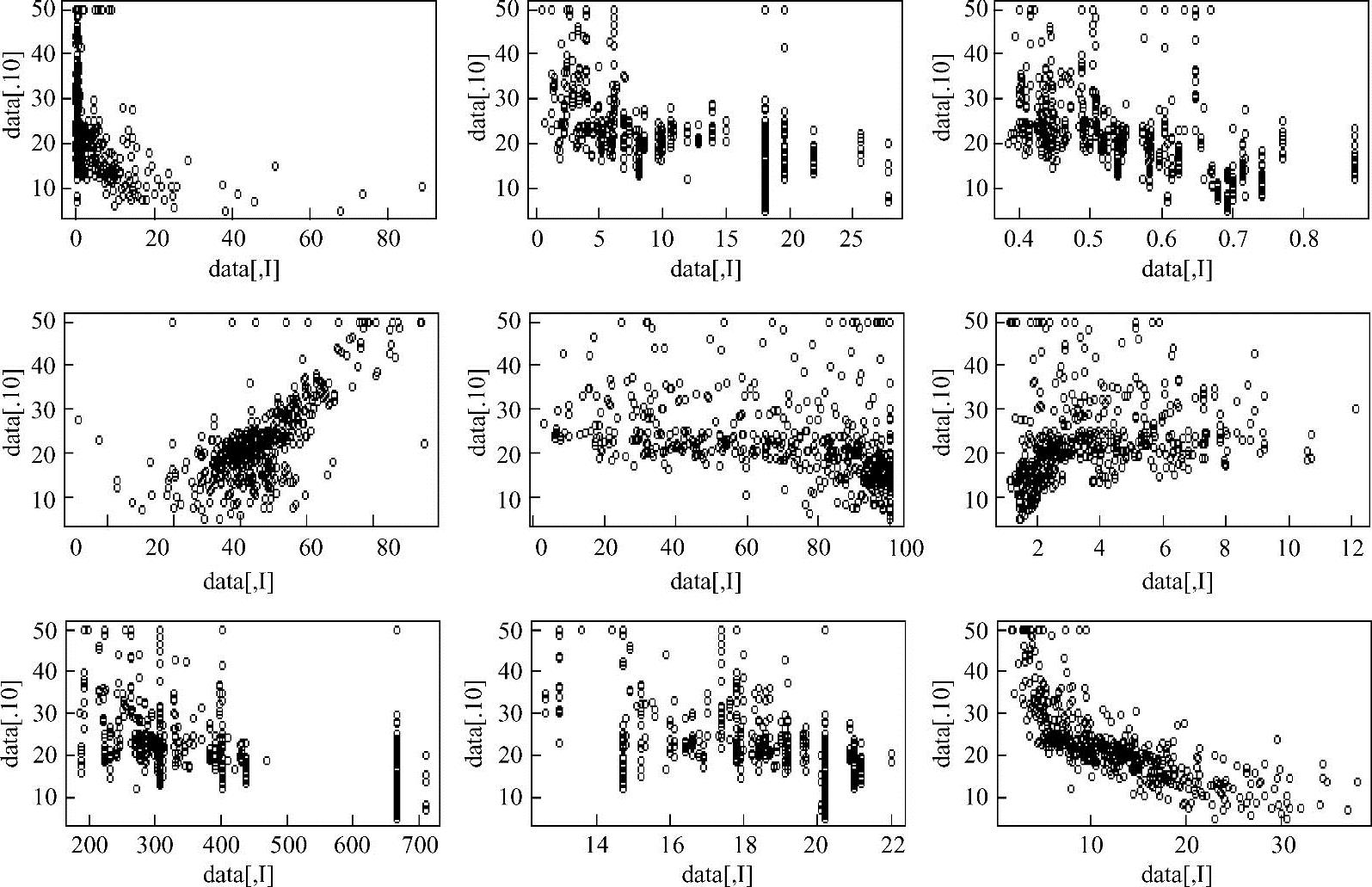
＞par（mfrow=c（3，3））
＞for（i in 1：9）{
＞ plot（data[，i]，data[，10]）
＞}
显示响应变量medv和输入变量之间的关系，如图2.11所示。
(www.xing528.com)
图2.11 medv和输入变量的关系
使用506行数据样本中的400个作为训练样本：
＞set.seed（2016）
＞n=nrow（data） #统计数据行数
＞train＜-sample（1：n，400，FALSE）#数据集中随机取400个样本作为训练集
注意，R对象train包含了训练样本中数据行的位置（下标）。它不包含实际观察数据。
（2）建模
使用neuralnet包的函数构建DNN，公式存储在名为f的R对象中。响应变量medv将针对剩余的九个属性“回归”。
＞f＜-medv～crim+indus+nox+rm+age+dis+tax+ptratio+lstat #存储公式
DNN可以使用神经网络函数进行拟合。实现如下：
注：如果想使用传统的反向传播，可以设置algorithm=“backprop”。如果使用这个选项，还需要指定学习率（即learningrate=0.01）。
（3）预测
DNN预测可以直接使用神经网络包提供的compute函数，唯一需要做的事情就是将它包含的DNN模型与测试数据传递过去，实施方法如下：
＞pred＜-compute（fit，data[-train，1：9]）
注意，-train是返回训练样本以外的行号。图2.12显示了线性回归（实线）的拟合值和预测值。虽然有一些离群值，但是该预测模型看起来相当好。这里可以通过性能标准来验证。接下来以计算平方相关系数、均方误差（mse）和均方根误差（rmse）为例进行说明：
＞round（cor（pred$net.result，data[-train，10]）^2，6）
[1，] 0.809458 #因为平方相关系数小于0.9，所以模型还有待提高
＞mse（data[-train，10]，pred$net.result）
[1] 0.2607601849
＞rmse（data[-train，10]，pred$net.result）
[1]0.5106468299
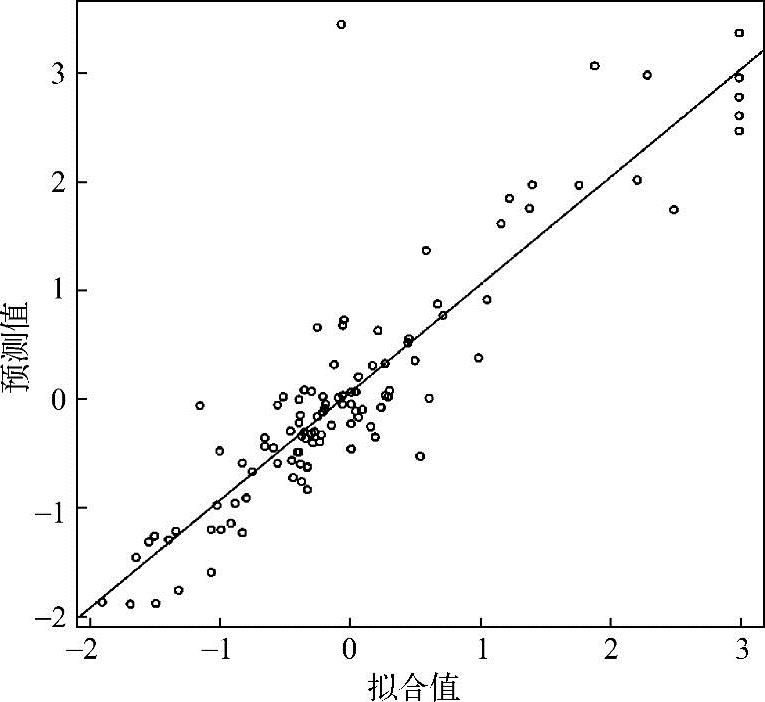
图2.12 预测值和拟合值
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
