用单层神经网络逼近函数y=x2

不久前，Hornik等人发现，一个隐藏层足以模拟任意分段连续函数。

Hornik定理：假设F是n维坐标系中的有界连续函数。那么存在一个两层神经网络F′，F′具有有限个隐藏层的神经元，这些神经元可以很好地表示F。也就是，对于F定义域内的任意x，都有F（x）-F′（x）＜ε。

定理意味着，对于任何连续函数F可以通过建立一个单隐藏层的神经网络来计算。至少在理论上，对于很多问题，一个隐藏层应该足够了。

当然，在实践中还是有些问题。首先，真实世界的决策函数可能不是连续的，对于非连续函数，这个定理没有指定所需的隐藏层的神经元数量。看来，对于很多实际问题，需要多个隐藏层来进行准确分类和预测。尽管如此，这个定理仍旧有一些实用的价值。

【例2.1】使用R来创建一个DNN实现函数y=x²的近似。

（1）加载用到的包

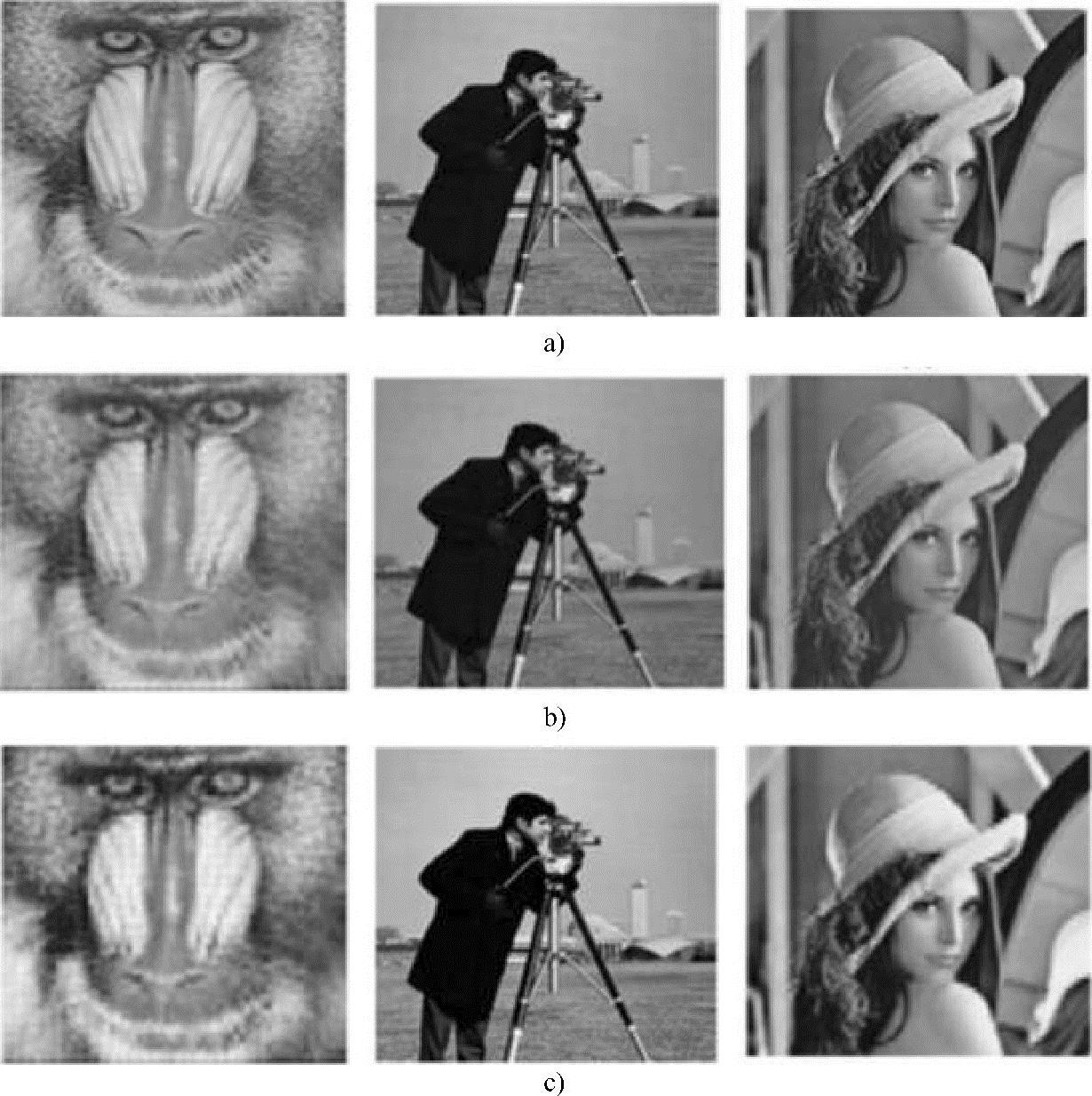
图2.5 基于DNN图像压缩结果

＞library（neuralnet）

（2）描述y=x2

＞set.seed（2016） #用来保证结果的重复性

＞attribute＜-as.data.frame（sample（seq（-2，2，length=50），50，

replace=FALSE），ncol=1） #attribute为属性变量x

＞response＜-attribute^2 #response为响应变量y

第二行产生了50个-2～2的观察值，其结果保存在R对象attribute中。第三行使用R对象response保存计算结果y=x²。

将attribute和response组合成数据框对象（用数据框表示数据是一个好办法，会使R编码变得简单）：

＞data＜-cbind（attribute，response）

＞colnames（data）＜-c（＂attribute＂，＂response＂）

查看数据的前10个观测值：

＞head（data，10）

attribute response

1-1.26530611.60099958

2-1.42857142.04081633

31.26530611.60099958

4-1.51020412.28071637

5-0.28571430.08163265

6-1.59183672.53394419

70.20408160.04164931

81.10204081.21449396

9-2.00000004.00000000

10-1.83673473.37359434

＞plot（data） #画出散点图

不出所料，响应变量正是属性变量的平方。它的可视化图像如图2.6所示。

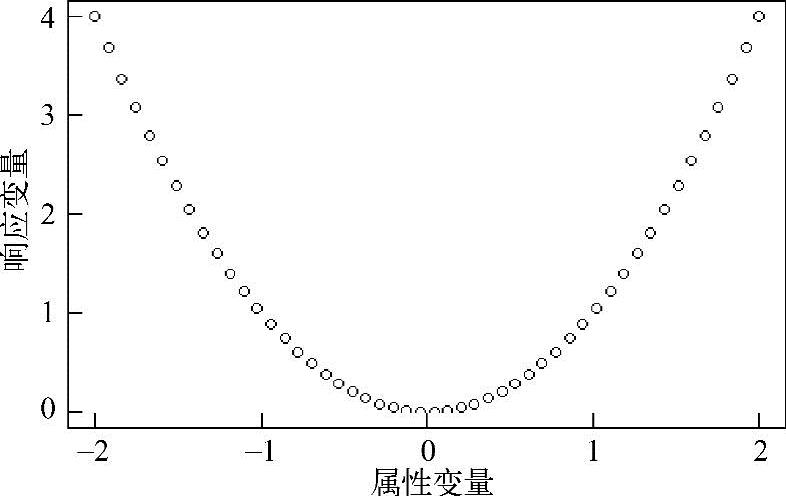
图2.6 y=x²模拟数据的图像

（3）建模(www.xing528.com)

建立一个包含两个隐藏层、每层由三个神经元组成的DNN，具体的方法如下：

＞fit＜-neuralnet（response～attribute，data=data，hidden=c（3，3），threshold=0.01）

公式response～attribute遵循标准的R实践，阈值很大程度上要根据应用的模型来定。图2.7显示的模型用了3191步使误差收敛到0.012837。

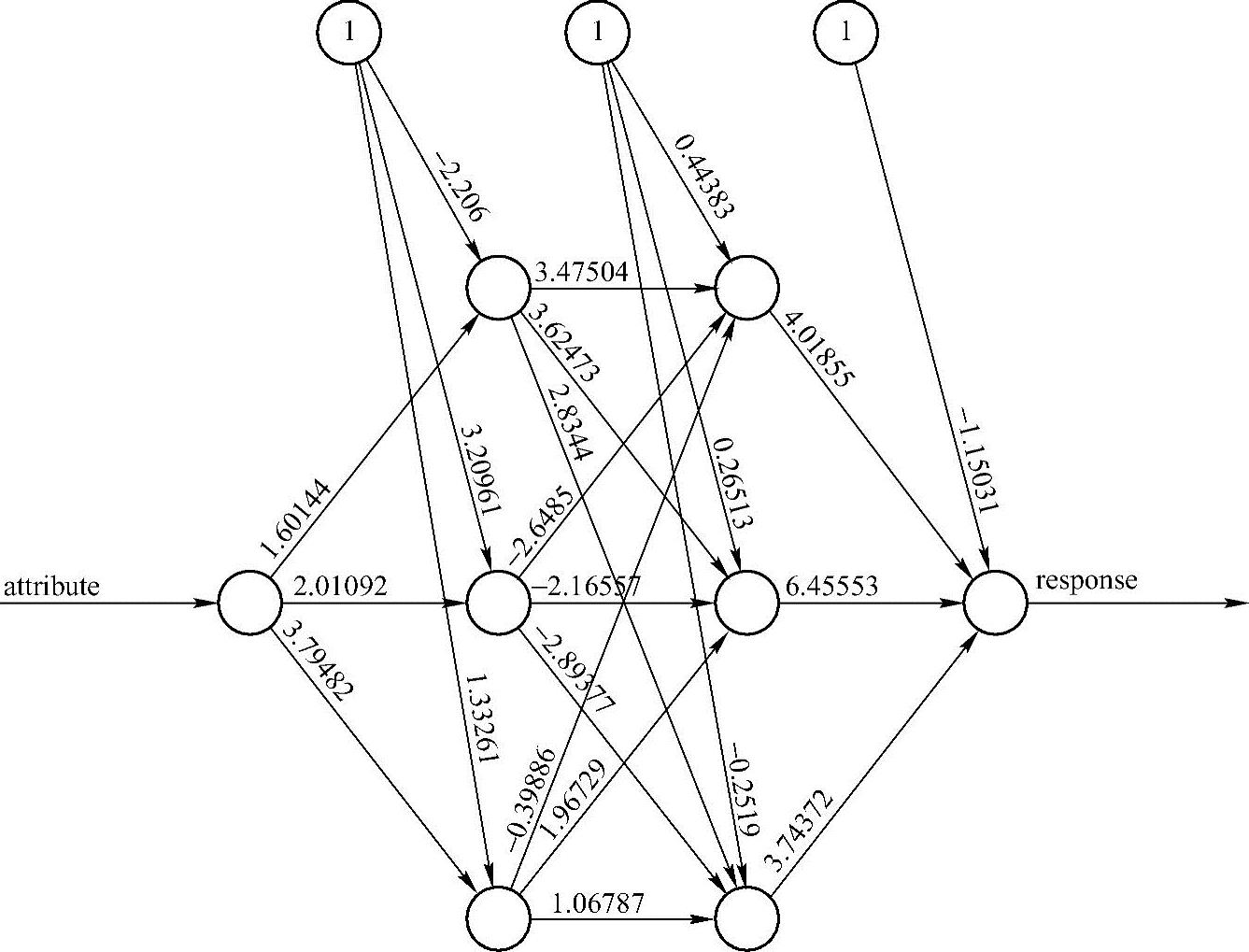
图2.7 y=x²的DNN模型

（4）模型部署

使用测试样本来看在进行函数近似时，模型是多么的好。在-2～2之间产生10个观察值，然后将结果保存在R对象testdata中。

＞testdata＜-as.matrix（sample（seq（-2，2，length=10），10，replace=FALSE），ncol=1）使用compute函数完成预测：

＞pred＜-compute（fit，testdata）

注意：想知道在R对象中哪些属性是可用的，只需要输入：

attributes（object_name）

例如，想要知道属性pred，只要输入：

＞attributes（pred）

$names

[1]＂neurons＂＂net.result＂

使用$net.result可以获取pred的预测值：

＞result＜-cbind（testdata，pred$net.result，testdata^2） #组合数据

＞colnames（result）＜-c（＂Attribute＂，＂Prediction＂，＂Actual＂） #命名列名

＞round（result，4） #精确到四位小数

Attribute Predication Actual

[1，] 1.55562. 40102.4198

[2，] 0.66670. 41830.4444

[3，] 0.22220. 06650.0494

[4，] -1.11111. 23461.2346

[5，] 2.00003. 95954.0000

[6，] -1.55562. 41872.4198

[7，] -0.66670. 43940.4444

[8，] -0.22220. 05250.0494

[9，] -2.00003. 94404.0000

[10，] 1.11111. 25631.2346

＞plot（result） #画出散点图

预测和拟合值如图2.8所示，数据显示DNN提供了一个很好的模型，虽然不确切，但十分接近实际的函数。

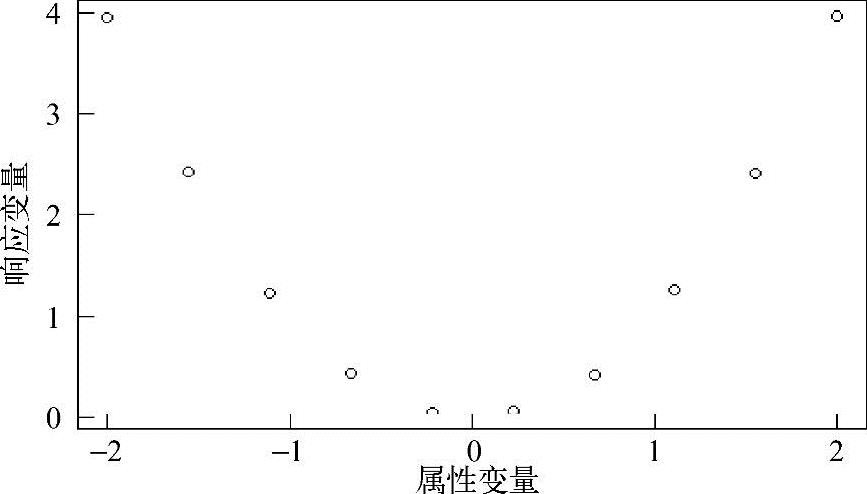
图2.8 DNN预测值和拟合值