学习算法：反向传播方法及误差评估

学习算法有很多种，一般而言，它们都是通过迭代修改网络权重，直到网络输出与期望输出的误差低于一个预先设定的阈值。

反向传播算法是最流行的学习算法，并且现在还在广泛使用。它将梯度下降法作为核心的学习机制。从随机权重开始，反向传播算法计算权重值是根据网络输出与期望输出之间的误差逐渐调整权重值。

这个算法将误差从输出端传播到输入端，并且使用梯度下降逐渐微调网络权重使误差值最小化。

学习步骤如下：

1）定义变量与参数：x（输入向量）、w（权值向量）、b（偏置）、y（实际输出）、y^（期望输出）和α（学习率参数）。

2）初始化：n=0，w=0。

神经网络通过随机设定权重值和偏置进行初始化。首要规则是将随机值设定在一个范围内（-2n～2n），这里n是输入特征的个数。

3）输入训练样本：对每个训练样本指定其期望输出：A类记为1；B类记为-1。

4）前馈：在网络中，信息从输入层到隐藏层再到输出层的向前传递，并且传递过程要借助激活函数和加权，计算实际输出y=σ（wx+b）。(www.xing528.com)

5）更新权值向量：利用梯度调整权重，以达到减小误差的目的。

每个神经元的权重和偏置都是按照一定规则调整的，这个规则依赖于激活函数的导数、网络输出与实际目标结果之间的差别以及神经元的输出。

图1.8粗略地说明了权重调整的基本思想。如果偏导数是负的，要增加权重（见图1.8a）；如果偏导数是正的，要减少权重（见图1.8b）。这种学习流程的每一个循环，称为迭代（Epoch）。

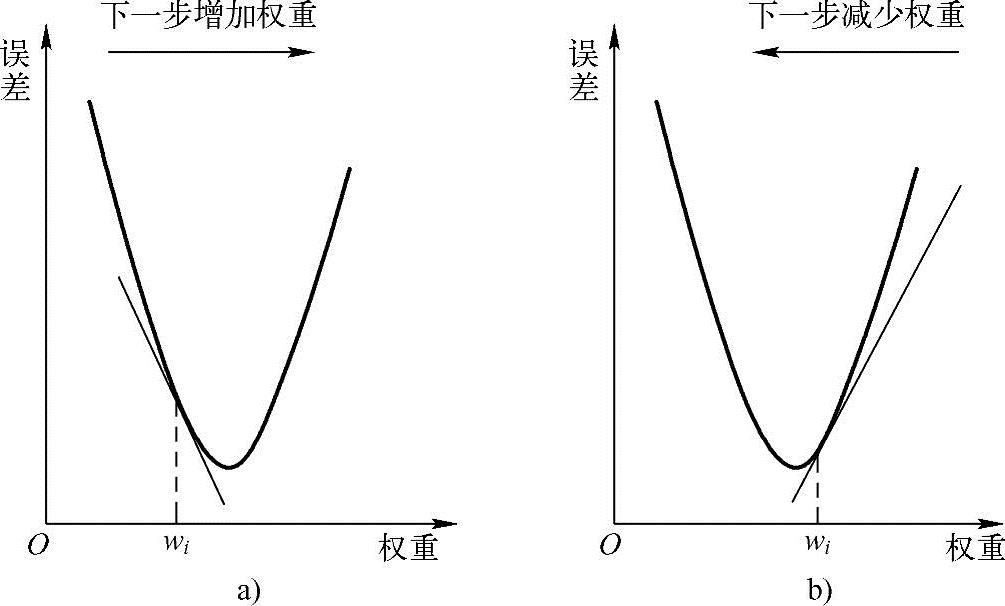
图1.8 反向传播算法的基本思想

6）误差评估：将网络输出与已知输出进行比较，以此评估网络权重。如果误差低于预先设定的阈值，网络训练完毕，并且算法终止，否则返回步骤3）。

早期使用梯度下降的反向传播算法经常收敛得很慢或者根本就不收敛。找到全局最优解，避免局部最小值，这是个挑战，因为，一个典型的神经网络可能有成千上万的权重，用这些权重的组合来求解。这个解经常是高度非线性的，这使得优化过程变得复杂。为了避免网络陷入局部最小，通常要指定一个动量参数。