常用的激活函数：双曲函数和线性函数

隐藏层结点需要激活函数实现非线性变换。一个神经元先执行激活函数，接着函数的输出传输到网络的下一层神经元。设计激活函数是为了限制神经元的输出，输出值通常被限定在0～1或者-1～1之间。在大部分情况下，一个网络中的每一个神经元的激活函数都是一样的。几乎所有的非线性函数都可以充当激活函数，尽管如此，对前向传播算法而言，激活函数必须是可微的，如果是有界函数，将会更有帮助。

双曲函数是一个常规的选择，这个函数是一个形如“S”的可微激活函数。双曲函数如图1.7所示，这里的c是一个值为0～1的常量，双曲函数很受欢迎，部分原因是求导容易，减少了训练时的代价。双曲函数的输出值也是在0～1之间，其表达式如下：

激活函数的数量很多，如

1）线性函数：

σ（x）=ax+b

2）双曲正切函数：双曲正切函数的输出范围是-1～1。这个函数与双曲函数有许多共同的特性；但由于其输出范围更大，有时候在对非线性关系建模时，其会更有效。它的函数表达式如下：

σ（x）=tanh（cx）

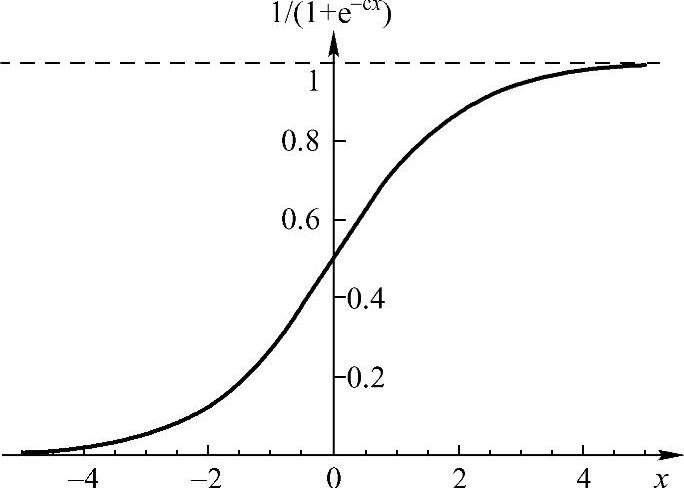
图1.7 双曲函数(www.xing528.com)

3）Softmax函数（Logistic-sigmoid、Tanh-sigmoid）：神经网络使用一个Soft-max函数来得到输出是很常见的。使用这个函数可以得到k个类别上的概率分布。其函数表达式如下：

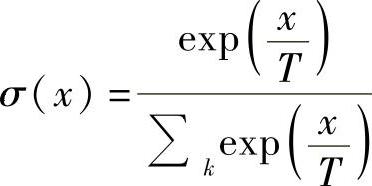
式中，T是温度（通常设定为1），它通常和一个具有k个类别的响应变量一起使用。基本上，它可以被看成一系列的二值结点，这些结点相互约束以便使k个状态中的某一个值为1，同时其余的状态值为0。

4）矫正线性函数（ReLU）：它的表达式如下：

σ（x）=max（0，x）

这个激活函数在深度学习模型中很常用，因为对于语音识别和计算机视觉任务而言，它显著改善了分类速度。只有在神经元的输出值是正数时，它才允许激活神经元。这个激活函数还能够使其所在网络的计算速度快于采用双曲激活函数或者双曲正切激活函数的网络，这是因为它只是一个简单的求取最大值的操作。矫正激活函数使神经网络稀疏，因为当随机初始化时，整个网络中的神经元大约有一半被设置成0。

还有一种平滑估计，表达式如下：

σ（x）=log（1+exp（x））