基础刚度对结构响应的影响

基础的整体刚度取决于土壤的强度和刚度以及结构基础构件。基础刚度是预测结构对风、波浪、地震载荷动力响应的基础。基础刚度一般而言随频率而定，这点在预测地震载荷动态响应时非常重要。

支撑基础结构的土壤通常具有有限的刚度，因此通常不能把土壤模化成刚性质量块。换句话说，不能假设基础结构具有固定支撑。在任何基础结构分析和风力机结构分析中，非常重要的一点是正确地描述由支撑土壤形成的实际边界条件。

为了在这类分析中描述支撑土壤的有限刚度，通常是建立一组所谓的基础弹簧模型，应用于所分析结构的一个或多个模拟支撑点上。这组基础弹簧可能包括与下述各种运动模态相关的弹簧：

1）垂直弹簧刚度；

2）水平弹簧刚度；

3）转动弹簧刚度；

4）扭转弹簧刚度。

土壤特性是非线性的，因此基础弹簧也是非线性的。通用的方法是采用线性弹簧刚度，这种情况下刚度值的选择，在所考虑的载荷工况下，取决于土壤所承受的应变水平。通常的方法是处理土壤的剪切模量G，这个等效剪切模量与初始剪切模量G₀有关，是剪切应变γ的函数，如图8-12所示。图8-12同时给出了土壤的阻尼比ξ，它是剪切应变γ的函数。

图8-12 剪切模量和阻尼比与应变

对于土壤三个最重要来源的动载荷，预计的剪切应变水平如下：

1）地震：最大的应变值可达10^-2～10^-1；

2）旋转机器：小的应变通常小于10^-5；

3）风和海浪：中等的应变可达10^-2，典型性值为10^-3。

下述的经验关式可以用于建立土壤的初始剪切模量G₀：

上式中σ₀′和G₀的单位都是kPa，A=3000±1000，具体取决于材料（尺寸、形状等）。OCR表示黏土的过固结比率，对于沙土设定为等于1.0。指数k是塑性指数I_P的函数，按表8-2给定。e是空隙比。

表8-2 指数k

限制有效应力σ₀′定义为3个主有效应力的平均值。

注意，地质学中有效应力定义成总应力减去孔隙压力。

对于砂可以采用下式计算：

上式中σ₀′和G₀的单位都是kPa，K按照表8-3取值。对于黏土，可以运用下列关系替代上式：

G₀=2600s_u

式中 s_u——土壤的未排水剪切强度。

表8-3 因子K

建立剪切模量和阻尼比的步骤如下：

1）确定动态载荷来源（地震、风、波浪以及机器振动）；

2）通过查图8-12，找到载荷预计的应变水平γ；

3）通过查图8-12，得到阻尼比ξ；

4）通过查图8-12，找到剪切模量比G/G₀；

5）根据土壤类型，选择上面给定的式子计算G₀；

6）G₀与G/G₀相乘计算G。

举例：对处于黏土中、未排水剪切强度s_u=200kPa承受风载荷的地基有：(www.xing528.com)

1）载荷来源是风；

2）预计的应变水平γ=10^-3；

3）阻尼比约为ξ=0.10～0.15；

4）剪切模量比G/G₀=0.35；

5）初始的剪切模量G₀=2600s_u=520MPa；

6）剪切模量变成G=0.35×520=180MPa。^[2]

表8-4提供了估计泊松比的指导。

表8-4 泊松比ν

一旦通过G₀和图8-12建立了等效剪切模量G，并估计了泊松比ν，就可以导出基础刚度。考虑下面4种刚度：

1）垂直刚度，K_V=V/δ_V，它表示垂直力V和垂直位移δ_V之比。

2）水平刚度，K_H=H/δ_H，它表示水平力H和水平位移δ_H之比。

3）转动刚度，K_R=M/θ，它表示倾复力矩M和滚动旋转角θ之比。

4）扭转刚度，K_T=M_T/θ_T，它表示转矩M_T和扭转角θ_T之比。

表8-5～表8-7中给出了各种形式基础的弹簧刚度公式，包括：

1）底座置于整个基岩层的筒形基础；

2）底座置于半个基岩层的筒形基础；

3）底座嵌入整个基岩层的筒形基础；

4）桩基础。

对于底座，假设它们相对于土壤是坚硬的，并且完全与土壤接触。在下面的讨论中假设桩基础是柔性的。

表8-5～表8-7中给出的弹簧刚度都是静刚度，也就是说它们是频率趋近于零时的刚度。动刚度可能会偏离静刚度，特别是在高频振动的情况下。然而，对于风力机基础的风载荷和波浪载荷，无论是陆上还是海上，诱导振动具有的特征是静刚度将代表结构分析中需要的动刚度。但是对于地震载荷，为了得到合适的动刚度值，有必要也应该考虑静刚度随频率的降低。

桩的长径比定义为L/D，其中L是桩的长度，而D是桩的直径。如果L/D＞10，大部分桩是柔性的，也就是说桩的有效长度小于L，桩端的响应与桩的长度无关。表8-7给出了3种理想土壤剖面和下述运动模态下柔性桩桩端的弹簧刚度：

1）水平；

2）转动；

3）水平-转动耦合。

表8-5 底座置于整个基岩层和底座置于半个基岩层的筒形基础

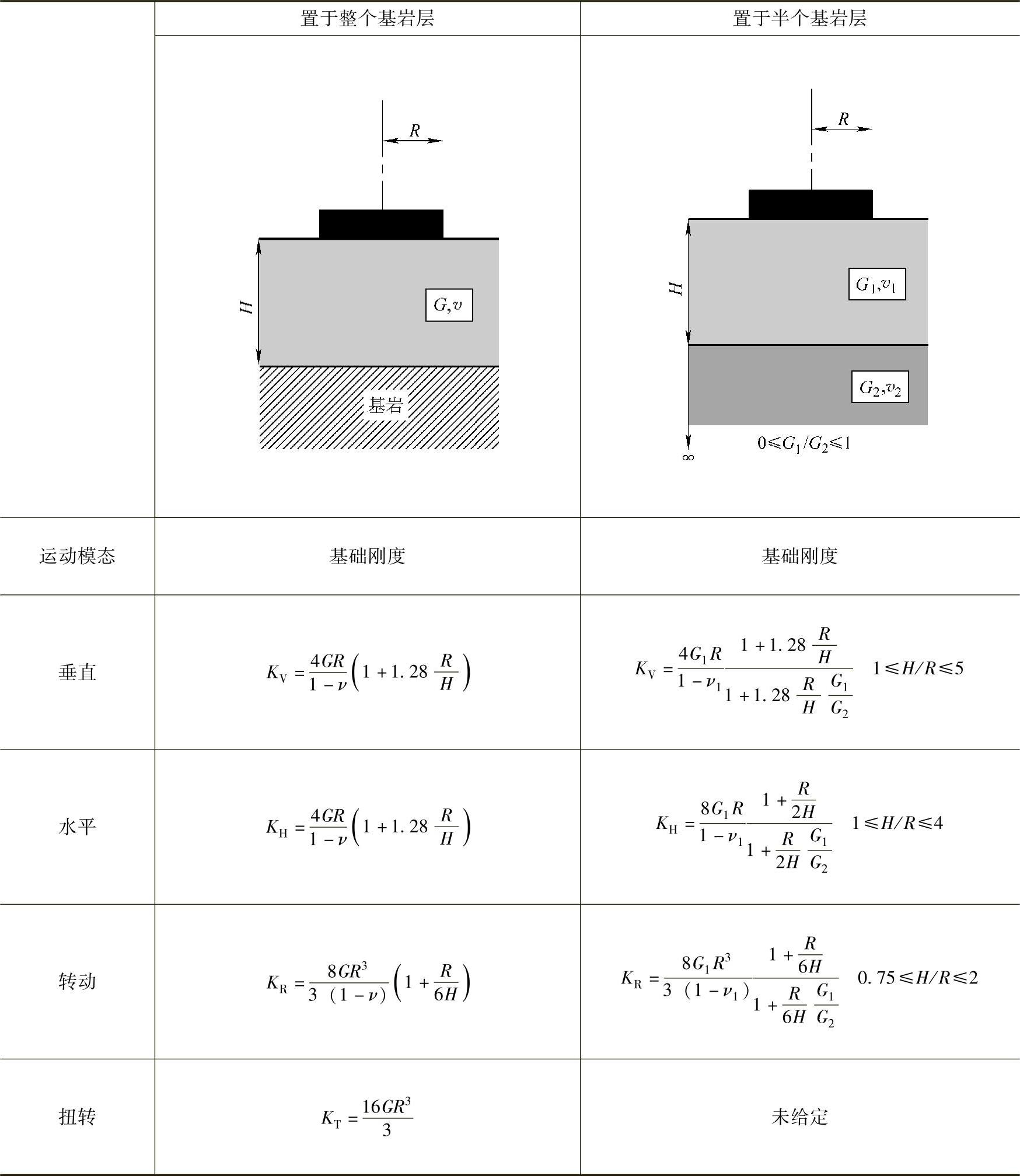
参考土壤的杨氏模量E与剪切模量G的关系为

E=2G（1+ν）

E_S是深度z等于桩直径D时E的值，而E_P是桩材料的杨氏模量。

这里给出的基础刚度公式可以用于计算风力机气弹分析中支撑塔架的弹簧刚度。根据经验方法，当用一个真实的、有限的基础刚度代替假设的刚性基础（端部固定的塔架）时，塔架的固有频率会减少0%～5%。在特殊情况下，这种误差可能达到20%。

表8-6 底座嵌入整个基岩层的筒形基础

表8-7 柔性桩