如何实现横向加载的桩？

分析横向加载桩最常用的方式是基于通常所说的p-y曲线方法。p-y曲线给出了当桩横向偏移距离y时，周围土壤阻力的积分值p之间的关系。桩模化成许多连续的梁柱元素，元素之间在节点处依靠非线性弹簧支撑。非线性弹簧在每个节点由一条p-y曲线描述，如图8-7所示。

对于顶端加载的桩，沿桩任意点桩位移和桩应力的解由桩的微分方程求解得到

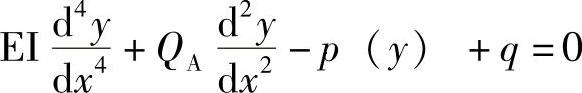
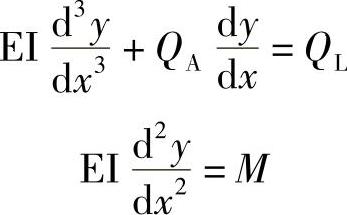
式中 x——沿着桩轴向的位置；

y——桩的横向位移；

EI——桩的弯曲刚度；

Q_A——桩的轴向力；

Q_L——桩的侧向力；

p（y）——横向土壤反作用；

q——沿桩分布的载荷；

M——在x位置桩的弯曲力矩。

梁柱具体模型如图8-8所示

有限差分方法通常是获得桩微分方程式最优解的最可行方法。有许多商业计算机程序可以进行这项工作，这些程序通常可以提供桩顶端受轴向力、横向力和弯矩联合作用的桩应力和桩位移的完全解，也就是按照上面介绍的t-z曲线方法轴向载荷沿桩逐渐传递到土壤的解。其中一些程序不但可以用于分析单桩，还可以用于分析群桩，包括可能的桩—土壤—桩的相互作用和桩顶端允许的适当的上层结构，不管是刚性桩帽还是有限刚度的结构。

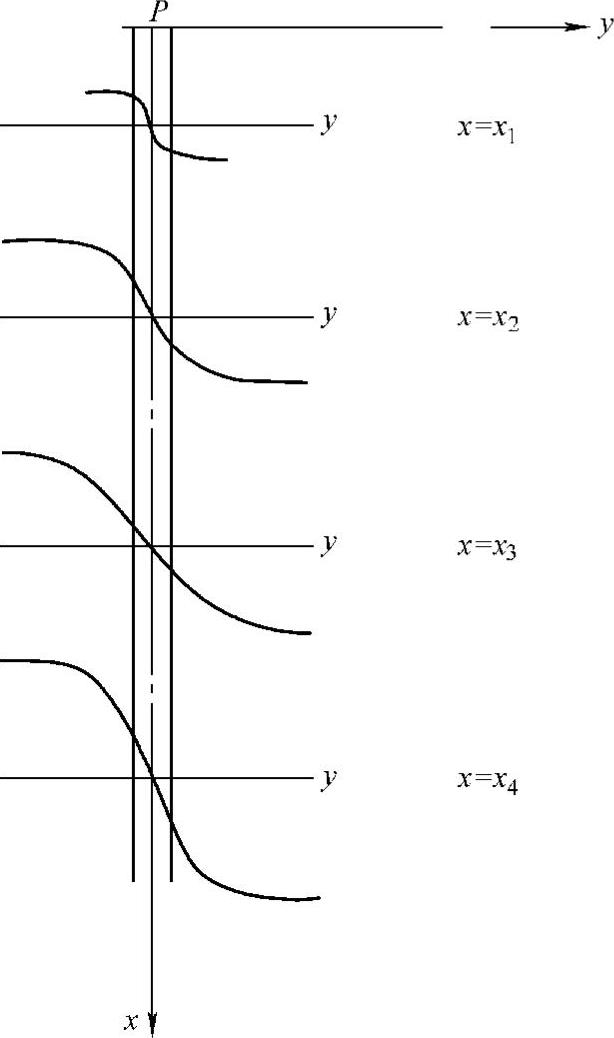
图8-7 表示桩的梁柱元素节点处的p-y曲线

有几种方法可以表示p-y曲线，它们是求解横向加载桩差分方程的基础。对于p-y曲线，应该考虑土壤类型、载荷类型、桩安装和冲刷的影响。p-y曲线构造过程最常用的是DNV（1992）和API（1987）中给出的方法。对于黏土中的桩，采用下述的DNV方法。对于砂，下面所述的DNV方法和API方法是一致的。

对于横向偏移y，桩单位长度上的横向阻力用p表示。单位长度的静态极限横向阻力用p_u表示。当桩发生横向偏移时，取p的最大值。

1.黏土

对于黏土中的桩，推荐按照下式计算静态极限横向阻力：

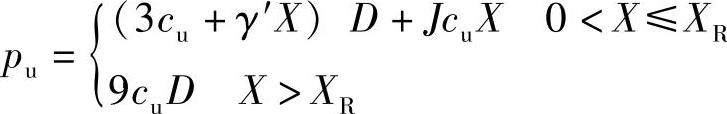
式中 X——土壤表层以下的深度；

X_R——过渡深度，低于这个深度，值（3c_u+γ′X）D+Jc_uX超过值9c_uD；

D——桩直径；

c_u——土壤未排水的剪切强度；

γ′——土壤的有效单位重量；

J——无量纲经验常数，它的取值范围为0.25～0.50，0.50推荐用于软正常固结黏土。(www.xing528.com)

对于静载荷，按下式生成p-y曲线：

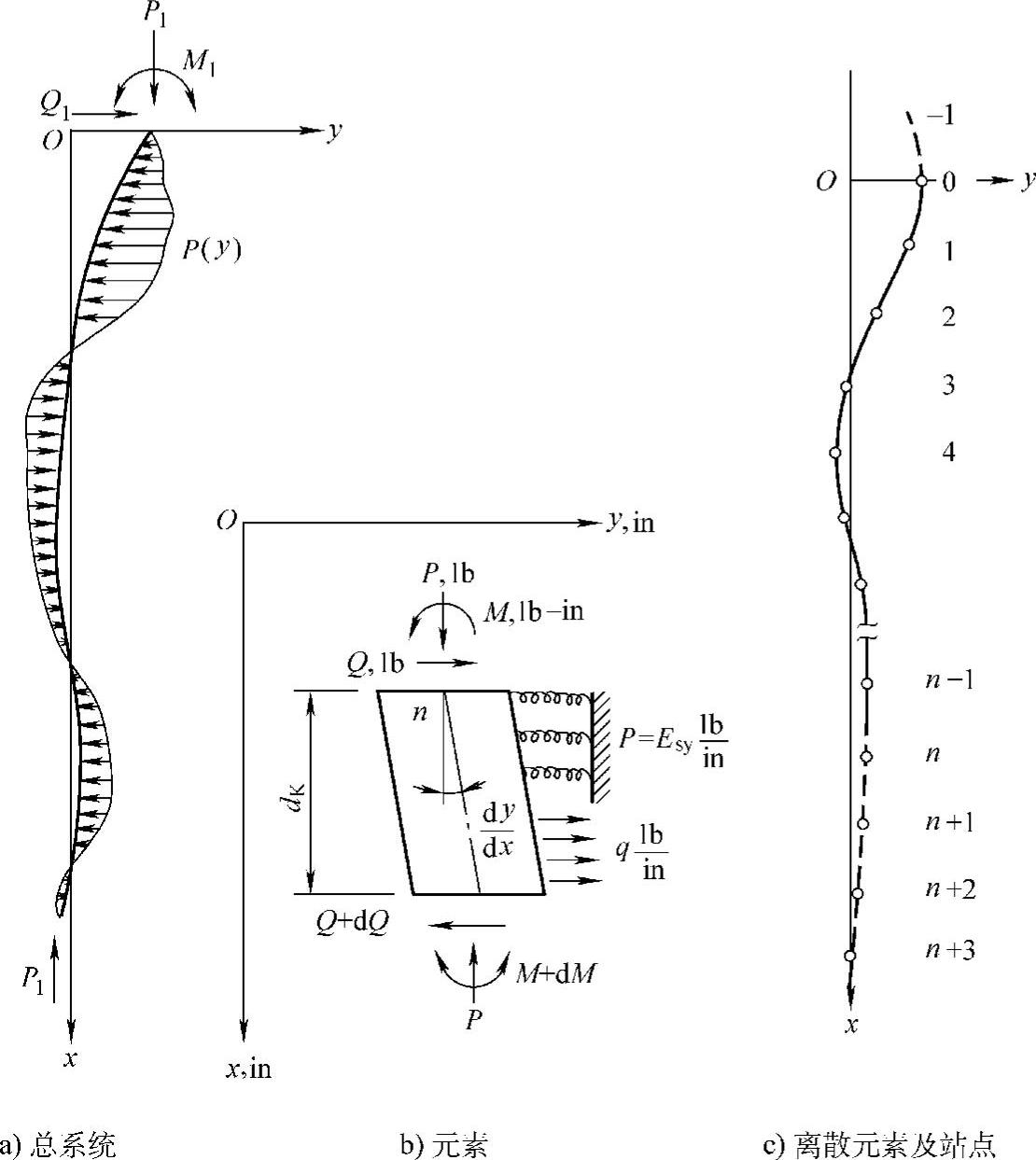
图8-8 梁柱的模型

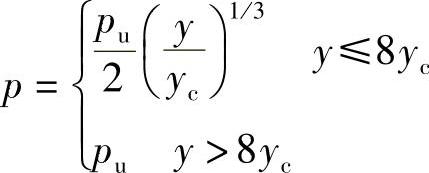
对于周期性载荷，且X＞X_R时，按下式生成p-y曲线：

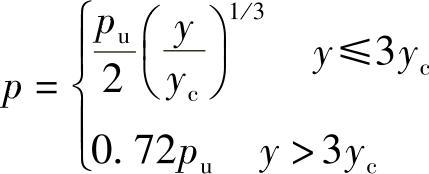
对于周期性载荷，且X≤X_R时，按照下式生成p-y曲线：

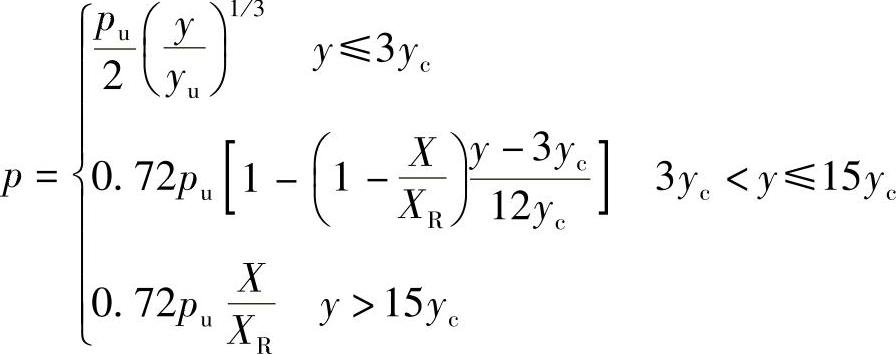
式中 y_c——y_c=2.5ε_cD，其中D为桩直径，ε_c为土壤原始样本在实验室未排水压缩试验中发生在最大应力一半值处的应变。

更进一步详细的内容，参考DNV（1992）。

2.砂

对于非黏土中的桩，建议按照下式计算静态极限横向阻力：

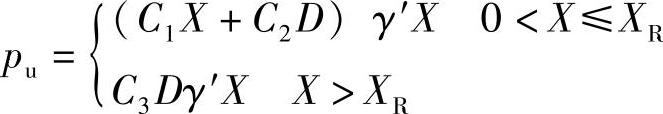
式中 C₁，C₂，C₃——取决于摩擦角ϕ，如图8-9所示；

X——土壤表层以下的深度；

X_R——过渡深度，低于这个深度，值（C₁X+C₂D）γ′X超过值C₃Dγ′X；

D——桩的直径；

γ′——沉积的土壤单位重量。p-y曲线按照下式生成：

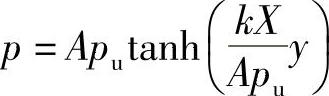
式中 k——次级反作用的初始模量，由摩擦角ϕ确定，如图8-10所示；

A——考虑如下静态载荷或周期载荷情况的一个因子：

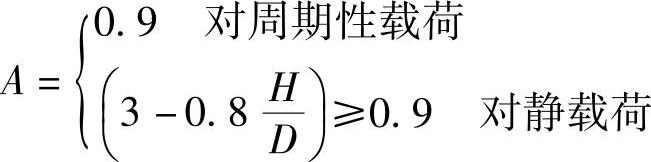
更进一步详细信息参见DNV（1992）。

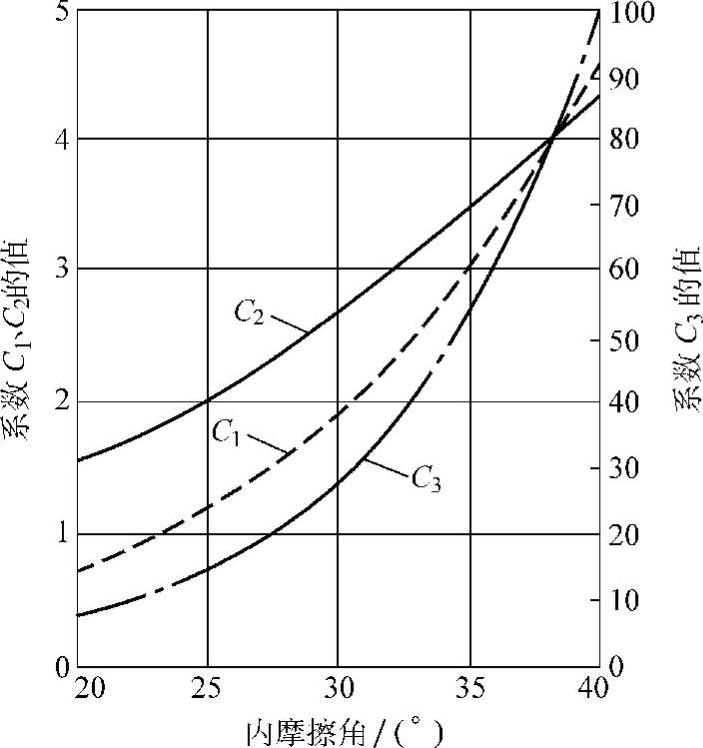
图8-9 作为摩擦角函数的系数