如何考虑疲劳强度影响因子K2的值？

疲劳强度可以用特定应力幅值的形式来表示，它导致在一定的等幅应力循环数以后会失效。这可以表示成S-N曲线的形式，也就是所谓的曲线，它给出了在一定的应力幅值S下失效的应力循环数。

各种各样的因素影响着由实验室小试样试验得出的参考强度值，这些因素绝大多数都会导致强度值减小。此处要强调的是，下面的因素非常重要，至少应该加以考虑：

1）技术尺寸效应；

2）几何尺寸效应；

3）表面硬化；

4）应力集中；

5）应力比R，定义成最小应力与最大应力的比值，拉应力定义为正，压应力定义为负。

1.技术尺寸效应

技术尺寸效应是指由同一种材料、不同尺寸的试样得出的疲劳性质不同所造成的减小。试样通常具有相对较小的尺寸（典型的尺寸是d=5～10mm），它们具有自己的力学性能，这些性能通过锻造或轧制减少了横截面积得到改进。技术尺寸效应可以使用针对疲劳强度的影响因子K₁来加以考虑，K₁可以通过图6-2得到。

图6-2 技术尺寸效应（d表示所考虑主轴部件的直径）

2.几何尺寸效应

几何尺寸效应造成的减少基于这样的事实，即不同尺寸的试样展示出不同的疲劳性质。它可以使用针对疲劳强度的影响因子K₂来加以考虑，K₂可以由图6-3决定。如果纯拉压的疲劳强度可以作为计算的基础，K₂可以设定成等于1。

3.表面硬化

疲劳裂纹常起源于不平整的表面或者细小的表面裂纹。试样理想的“参考表面”应该是抛光表面，表面粗糙度R_a=0.05～0.1μm。精细机械加工的表面粗糙度R_a=0.4～16μm。考虑表面条件效应的收缩因子K_r，可以由参考表面导出，通过图6-4来确定。

图6-3 几何尺寸效应（d表示所考虑主轴部件的直径）

注意，R_a表示的是平均表面粗糙度。在一些有关的文献中给出的是峰值粗糙度R_z而不是R_a。R_a和R_z之间有确定的关系，但是作为初步计算，可以认为峰值粗糙度R_z近似等于6R_a。

图6-4 收缩因子K_r与表面粗糙度R_a

4.应力集中

应力集中发生在局部几何形状发生变化的区域，如横截面积发生变化的地方，也可以出现在红套过盈的联轴器以及过盈配合的轴承处。各种常见形状应力集中系数的数值在Peter-son（1974）的相关研究文献中已给出。这样的应力集中对材料的敏感性主要取决于材料的屈服极限与强度极限的比值，以及结构上所考虑零件上的应力梯度。这种所谓的缺口敏感性可以采用缺口敏感因子q来考虑。

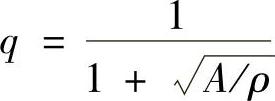
式中 ρ——缺口半径；

A——Neuber因子，可以由图6-5决定。

注意，缺口半径在图6-6中以“r_c”的形式出现。

如果遇到缺口，就用缺口敏感因子q把应力集中系数α转换成实际应用的缺口因子β，即

β=1+q（α-1）

常见的缺口是退刀槽，它传递来自主轴承的轴向载荷。轴承附近主轴的常见结构如图6-6所示，包括几何尺寸的数据见表6-1。

表6 - 1 包括几何尺寸的数据

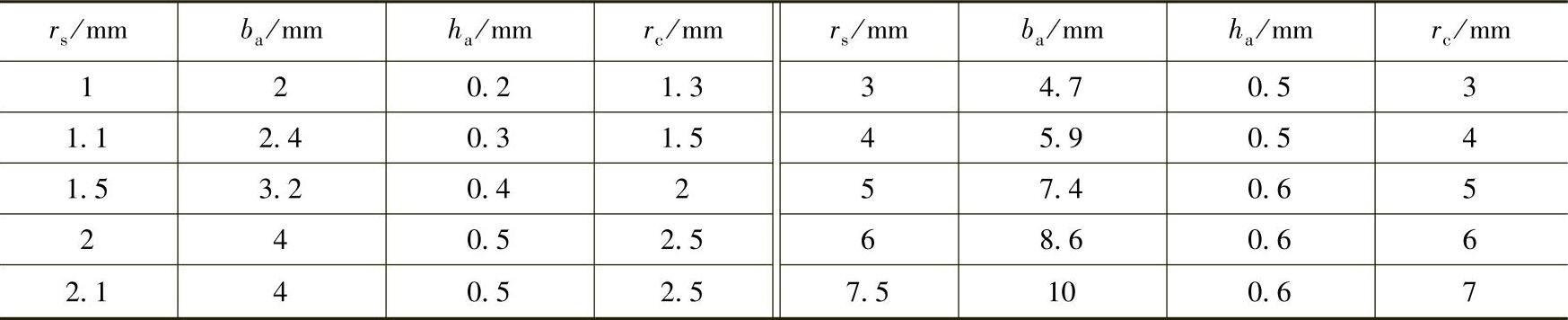
图6-5 缺口敏感因子q

图6-6 轴承附近的主轴结构

几何应力集中系数表示成α由图6-7和图6-8决定。

用于图中的符号如下：

1）D：主轴的大直径；

2）d：主轴的小直径；(www.xing528.com)

3）h：（D-d）/2；

4）r：缺口半径。

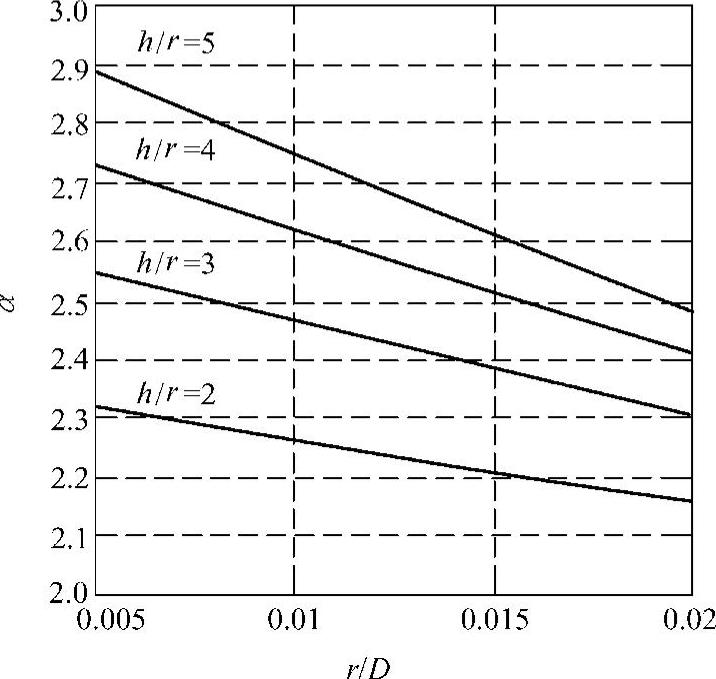
图6-7 应力集中因子（一）

由于轴承紧配合造成的应力集中，对应于ISO 286轴的间隙从m到r，可以采用应力集中系数α=1.1～1.2来考虑。

对于红套过盈配合的联轴器，应力集中系数采用α=1.7～2.0。

5.名义应力的影响

绝大多数材料的数据都是通过完全相反的弯曲试验或者脉动拉压试验得到的，如应力比R=σ_min/σ_max为-1。对于扭转试验R也等于-1。如果已有的试验中其他应力比占主导，则必须减少最大许用应力范围。然而，对主轴应力比常假定在-1附近，因此可以不必考虑任何这类的减少。在更准确的计算中，可以采用针对这个目的已有方法来考虑名义应力的影响，如Haig图。参见Gudehus和Zenner（1999）、Bergmann和Thumser（1999）以及VDI的相关研究。

6.抗疲劳性和特征S-N曲线

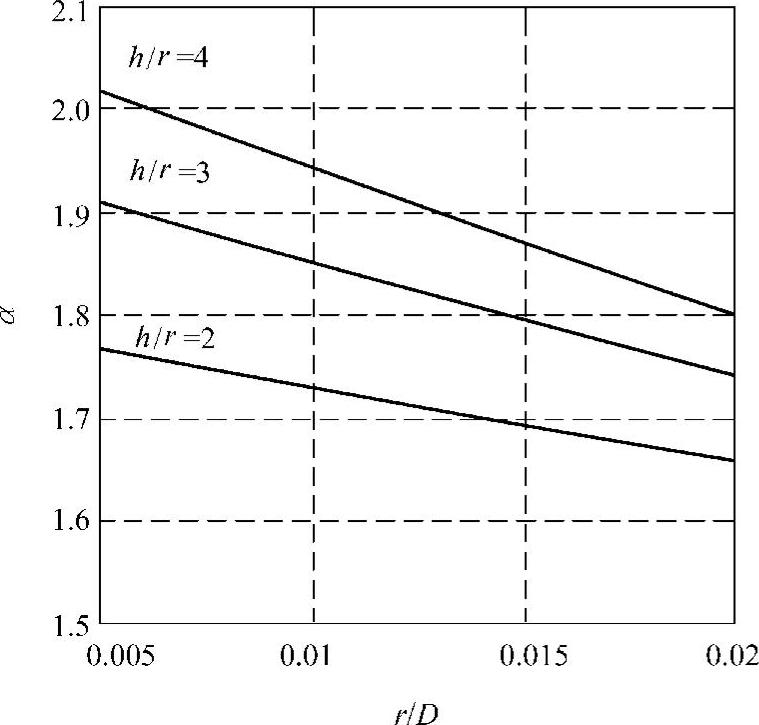
图6-8 应力集中因子（二）

当缺少实际材料的耐久试验时，有几种不同的方法用来构造人为的特征S-N曲线。每一种方法都有其各自的优点和缺点，有些方法可以在Gudehus和Zenner（1999）、Bergmann和Thumser（1999）以及（1998）的相关参考文献中找到。关于疲劳计算总的方面见附录C。总的来讲，不推荐采用两种方法的组合，因为这会导致对总体安全水平评价变得不清晰。

下面给出了其中一种构建特征S-N曲线的方法，仅供参考。它比较简单，适合用于初步计算。

对合金钢材料，建立S-N曲线可能比较困难，试验假定往往并没有很好说明。如果对所采用的钢种没有可靠的S-N曲线，可以采用人工的S-N曲线。它基于材料的静强度数据结合在旋转弯曲及扭转条件下（也可能是抗压）的疲劳强度σ_D，对标准的参考材料总会有这样的数据。如果对实际材料没有σ_D，对拉压情况可以采用下面的估算方法，方法基于带50%失效可能性的S-N曲线：

σ_D50% =0.436×R_e+77

式中 R_e——屈服强度（MPa）；

σ_D50%——单位为MPa，适用于材料为低碳钢或低合金钢的小尺寸7～10mm的抛光试件。

为了得到对应于2.3%的失效概率而不是50%失效概率的结果，σ_D50%必须按下式减小：

σ_D2.3%=σ_D50%-2s

式中 s——标准偏差。对低碳钢和低合金钢，s可以视为等于σ_D50%的6%，参见（1998）相关研究。

7.设计S-N曲线的确定

如果以lgS-lgN作为坐标轴，S-N曲线可以认为从（10，R_m）到（10⁶，σ_D）线性减小，此处R_m表示极限强度。当N＞10⁶时，曲线可以被视作水平线S=σ_D。

在结构承受疲劳载荷时，超过屈服强度的应力是不允许的，结果S-N曲线就在R_e处被切除掉。

由于轴上各点的影响因子是不同的，因此在轴上每一个不同的位置S-N曲线的应用是不一样的。

从保守角度讲，可以使用下面的设计准则：

σγ_f＜σ_D2.3%K₁K₂/（K_rβγ_m）

τγ_f＜τ_D2.3%K₁K₂/（K_rβγ_m）

式中 σ、τ——观察截面上的实际特征正应力和扭应力；

σ_D2.3%——持久极限的特征值，按上面的规定由σ_D50%计算得到。

对缺口因子β，考虑低应力循环次数时，材料对于缺口具有较低的敏感性，可以得到更好的近似。在N=10时，可以设定β=1，然后让β随lgN线性增加，直到N=10⁶时β=1+q（α-1），如图6-9所示。

疲劳载荷通常是以应力幅值分布的形式规定的，如所谓的“载荷谱”，它是以离散的形式给出在合适的离散应力幅值轴上每一个间隔内的应力循环数。每一个应力幅值间隔内的应力循环对总的疲劳损伤都有贡献。总的疲劳损伤可以根据Palmgren-Miner方法计算，它必须小于1.0以确保主轴的设计寿命失效概率足够低。参见附录C。

当主轴弯曲和扭转同时发生时，可以采用参考应力加以考虑，即

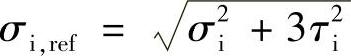
式中 σ_i——正应力；

τ_i——扭转应力。

如果弯曲应力以应力比接近-1的方式波动，同时剪切应力在正应力比0～0.8之间波动，采用参考应力σ_i，ref作为近似。更准确的方法可以在Gudehus和Zenner（1999）相关参考文献中找到。

图6-9 缺口因子