如何进行强度分析及其影响因素？

必须针对所有相关的载荷工况对风轮叶片进行结构分析，验证叶片的强度足以承受这些载荷工况下作用在叶片上的载荷。通过这些分析过程中的强度计算，验证给定设计寿命下的极限强度和疲劳强度是足够的。对受压结构部件，还要考虑到抗屈曲的稳定性。

对每一个载荷工况，将载荷部分安全因子乘以对应的特征载荷建立一组设计载荷。当用文档记录设计载荷时，应该引用相应的设计标准。从理论上讲，每一个载荷工况可以用6个载荷分量以及沿叶片展向的变化来定义。描述这种变化的精度必须足够好，以保证在叶片所有感兴趣的点都有足够精确的计算，特别是在所有的关键截面，如几何形状或材料发生变化的截面。

对材料性能产生影响的环境条件也应该加以考虑，特别是湿度和温度，它们均会导致强度和刚度的降低。在强度分析中，它们对设计的影响，通过选用适当的部分安全因子乘以特征效应来计算。

对关键部件的载荷，如叶尖制动，它的载荷在性质上跟叶片的普通载荷不同，这需要特别加以注意。

由于叶片越来越大，在翼梁、前缘和尾缘之间存在大的无支撑的面板，这对叶片的稳定性有影响。因此，除了全尺寸试验外，必须通过单独的计算验证叶片的抗屈曲能力。这种计算通常需要采用有限元分析，另外也需要考虑翼梁的屈曲问题。

叶片越来越长，对非刚性面板进行抗屈曲的稳定性评估变得更加重要。

1.标准

以下标准通常用于风力机叶片检查：

1）DS472。《风力机结构的载荷和安全》丹麦，DS472，1版，丹麦化学、土建、电子和机械工程师学会，丹麦哥本哈根，1992。

2）DS456。《非饱和聚酯增强玻璃纤维结构的应用》丹麦，DS456，1版，丹麦化学、土建、电子和机械工程师学会，丹麦哥本哈根，1985。

2.极限强度

如果载荷的方向与时间有关，就应该给出相位和频率的信息。对沿叶片展向的每个感兴趣的截面而言，必须计算它的设计载荷。理论上，必须计算全部6个载荷分量。一般情况下，弯矩和剪切力是最关键的，但在某些情况下，扭矩和轴向力对设计也很重要。

一旦有了有关材料强度和刚度、叶片几何形状及铺层必要的信息，叶片的承载能力就可以逐个截面进行计算。这些计算可用手工来完成，也可以用经过校验的有限元程序来完成。从理论上讲，所有的6个承载分量都需要进行计算，如叶片挥舞方向和摆动方向的抗弯能力。若采用材料强度特征值作为输入，得到的就是特征承载能力。那样设计承载能力就等于特征承载能力除以材料因子，即材料部分安全因子，参见2.3节。

一般地，沿叶片展向每个重要截面都应该进行检查，包括检查这些截面的6个载荷分量，以确保计算的设计载荷值不超过相应的设计承载能力。

本章中，需要着重考虑的强度是沿纤维方向的抗拉强度σ_F，T，这个强度主要由纤维束的强度σ_F，B来决定。纤维束的强度σ_F，B与各个纤维的平均失效应力σ成正比，即

式中 m——材料常数；

Γ——伽马函数。(www.xing528.com)

请参见Beaumout和Schultz（1990）相关研究。单个纤维强度σ通常遵循威布尔分布，但是根据中间限制法则，它们的平均值将遵循一个正态分布。因此，可以推出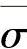和σ_F，T符合正态分布。如果采用σ_F，T分布的特定低尾分位数的值作为σ_F，T的特征值，σ_F，T的正态分布先决条件就很重要。应注意，如果假设σ_F，T分布符合威布尔分布，那么就可能导致σ_F，T特征值有一定错误。

强度性能的特征值通常定义为性能概率分布中特定分位数的数值。这经常是分布的低尾分位数，如2%或5%分位数。注意，不同的标准可能定义不同的特征值。例如，在不同的标准中，它不总是定义成同样分位数的值。因此，根据不同的标准，对于设计的特征值可能采用不同的部分安全因子。例如，DS472定义FRP材料特征值为5%分位数的值，其相应所要求的材料因子为1.7；但是DS456定义的特征值为10%分位数的值，相应的材料因子为1.8。设计中，未知的强度性能特征值应当与正确的部分安全因子相对应。把一个标准的特征值和另一标准的部分安全因子结合在一起是不正确的，这可能导致错误的结果和不安全的设计。

3.稳定性

叶片越长，叶片的抗屈曲稳定性代替极限强度控制叶片设计的可能性就越大。叶片的抗屈曲稳定性很容易采用经过校核的有限元程序进行计算来验证。由于叶片几何形状的复杂性，对于求解屈曲能力封闭形式解这样的问题，缺乏有效的工具，用手工完成这个验证计算是相当困难的。

为使抗屈曲设计有足够的安全性，标准的方法是增加设计安全裕量，以弥补几何形状不完整性、纤维的错位、工艺操作影响等不利因素。

4.疲劳强度

文档记录显示，必须具有足够的疲劳强度，它适用于沿叶片的所有截面以及每一位置处的所有方向。为此，应给出沿叶片相关点的所有载荷分量，包括相位和频率信息。如果给出6个载荷分量的时间序列，这种要求就可以自动得到满足。根据6个载荷分量的时间序列，可得到所有相关点的长期应力分布。理论上，它包括平均应力分布和表示相对平均应力变化的应力范围的分布，通常采用雨流计数法。设计寿命内的应力循环总数可以根据时间序列得到，并把应力范围分布转换成设计寿命内应力范围的柱状图谱。为此，需要选择一个合适的表示离散应力范围的轴。

沿叶片的每个截面，必须确认没有超出疲劳强度范围。实际中通过检查Miner累积损伤来完成，Miner累积损伤通过设计应力范围柱状图谱结合材料S-N曲线计算，通常这个累积损伤值不能超过某一临界值，一般是1.0。更多信息详见附录C。

在摆动方向的弯曲疲劳主要由重力载荷决定，它在很大程度上取决叶片的重量和设计寿命期间风轮的实际旋转次数。挥舞方向的弯曲疲劳由叶片对风所产生的气动载荷的响应来决定。注意，除正常运行载荷外，起动/停机的瞬态载荷以及由于偏航误差产生的载荷可能产生很大的累积疲劳损伤，需要全面考虑。疲劳计算和疲劳设计的示例，参见2.3.7节。

5.频率

至少，应该计算风轮叶片在挥舞方向和摆动方向振动的最低的两个特征频率。这些特征频率应与风轮的旋转频率相比较，与这些频率之间应有足够的裕量以避免叶片共振。建议特征频率在旋转频率±12%范围之外。

6.设计工具校验

其最基本的是采用经过验证并经过适当校验的设计工具。特别是在采用高级计算机程序的情况下，如有限元程序，重要的是针对风轮叶片全尺寸得到的试验结果对所采用的计算机程序模型进行调试校验，从而获得尽可能反映实际情况的模型。由于从一个叶片模型得到的校验不能自动传递到另一种型式的叶片，因此在对模型校验结果进行一般化处理时，需要特别注意。

7.分层

如果纤维增强铺层的抗剪强度不足以承受叶片中的剪切载荷，那么会发生脱胶分层现象。在这种情况下，重要的是考虑在垂直于叶片的方向上也要有足够的纤维强度。