海洋工程设计中的波浪载荷分析

1.波浪气候

通常在典型的3h时间段内，一个地方的波浪气候被认为是静态的。波浪气候由有效波浪高度H_S和峰值周期T_P表示。有效波浪高度H_S是衡量波浪气候强度的物理量，定义为海面上升量η标准偏差的4倍。另有一些资料把有效波浪高度定义为最大1/3倍波高的平均值。对于窄带高斯海面上升过程，这两种定义是趋于一致的。峰值周期T_P与海面上升过程的零均值周期有关。在3h周期内，有效波浪高度H_S和峰值周期T_P可视为常数。

H_S和T_P的长期分布由场址决定。H_S的长期分布通常可以由威布尔分布很好地表示，而由H_S确定的T_P分布可以由对数正态分布很好地表示，其对数正态分布的分布参数为H_S的函数。在Bitner-Gregersen和Hagen（2000）相关研究中可以找到其示例。

2.波谱

海面变化过程的频率成分可由功率谱密度表示。海面变化过程的谱密度可以用JON-SWAP谱表示，即

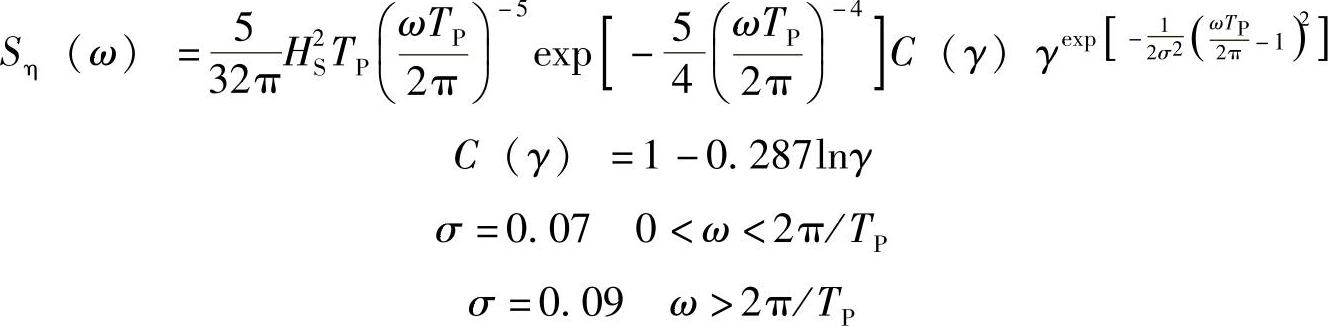
峰值加强因子γ可以表示为

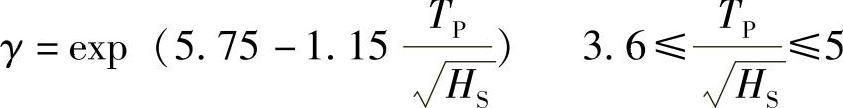
上式中H_S单位为m，T_P单位为s。峰值周期T_P和零交叉周期T_Z的关系可近似表示为

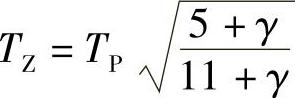
可参考Gran（1992）和DNV（2000）相关研究资料。

3.波高

在深水中，海面变化过程_η是一个高斯过程，从波谷到波峰的波浪高度H符合瑞利分布，H_S由下式确定：

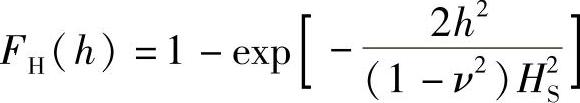
式中 ν——谱宽度参数。

在一段时间间隔T_L内的最大波浪高度H_max通常是设计感兴趣的。令N表示在这个时间间隔内海面变化过程的零交叉数，即N=T_L/T_Z。这样H_max分布可近似表示为

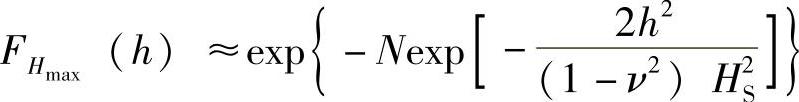
最大波浪高度的期望值可表示为

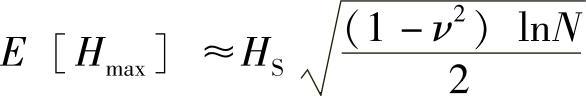
取其一阶近似值可以得到谱宽度参数ν=0.43。当ν=0.43时，最大波浪高度H_max和最大波峰Z_max的关系可表示为

H_max≈1.8Z_max

在浅水区，浅滩效应是指波峰变得更尖，波谷变得更平而不是更深，海面变化过程变得有些“偏斜”并且不再是一个严格的高斯过程，每个波浪高度也不再符合瑞利分布。现在已有办法可以解决由浅滩引起的偏斜现象。参见Winterstein等人（1991）以及美国陆军海岸工程研究中心（1973）相关研究。

注意在浅水中，波浪高度受水深d的限制。在水深d下，最大可能的波浪高度近似等于水深，即

H_max，lim≈d

波浪高度的瑞利分布将在上游发生畸变扭曲，从而趋近于这个极限。

4.波浪周期

一旦给定有效波浪高度H_S，零交叉周期T_Z通常由平移的对数正态分布表示，即

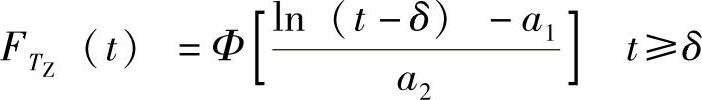
式中 Φ——标准正态分布函数；

a₁，a₂——分布参数a₁和a₂是H_S的函数；

δ——平移参数，可近似表示为

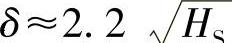
上式中，H_S的单位为m，δ的单位为s。这是基于制动考虑的，参见Haver（1990）相关研究。

平均零交叉周期T_Z指的是与给定有效浪高H_S对应的平均波浪周期。与最大波浪高度H_max对应的波浪周期T通过龙格特-希金斯（Longuet-Higgins）分布来表示：

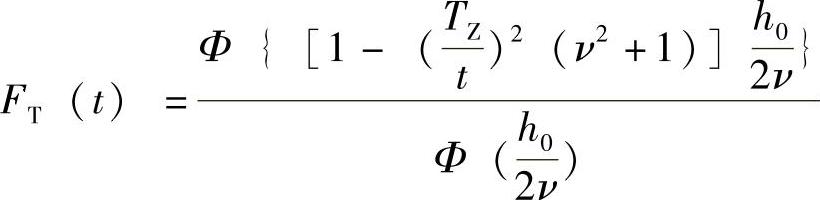
式中 Φ——标准正态分布函数；

ν——前面所述的谱宽度参数；

h₀——深水中正则化最大波浪高度，即

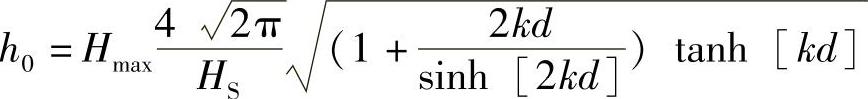
式中 k——波的数量，它是下述隐式方程的解：

ω²=gktanh[kd]

式中 L——L=2π/k，波长；

ω——ω=2π/T，角速度；

g——重力加速度；

k——波的数量；

T——波浪周期。

5.由莫瑞斯（Morison）方程计算波浪力(www.xing528.com)

瘦长结构部件，如淹没在水中的圆柱，作用在其上的波浪力可以利用莫瑞斯方程来预测。利用这个方程，z坐标上结构垂直单元长度dz上的水平力表示为

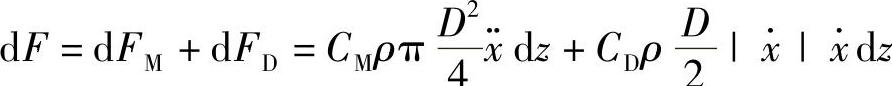
式中 C_M——惯性系数；

C_D——阻力系数；

D——圆柱直径；

ρ——水的密度；

——水的水平波浪诱导速度；

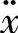——水的水平波浪诱导加速度。

公式的第一项为惯性力，第二项是阻力。高度z从静止水体开始计量，z轴向上，因此在海床上当水深为d时z=-d。结构的运动被认为非常微小。

根据一阶线性波浪理论，水平波浪诱导速度为

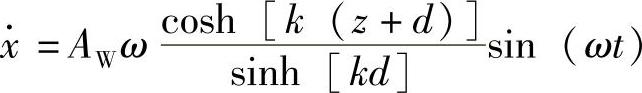
加速度为

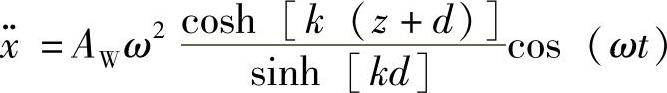
式中 A_W——波浪幅值。

在圆柱体上的水平力F可以利用莫瑞斯方程在z方向上从-d～0积分求得，即

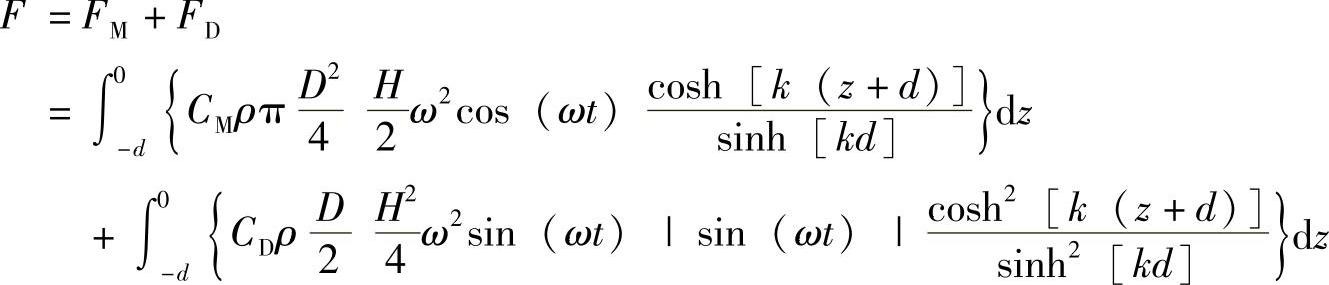
注意，-d～0的积分忽略了静止水体z=0以上波峰力的贡献。这对于惯性力F_M有一个小小的问题，因为当节点线在经过结构的静止水位线时惯性力会达到最大值。另一方面，阻力F_D在波峰通过结构时达到最大，这样如果这个力是主要载荷，忽略波峰的贡献将会导致很大的误差。

注意，只有当结构尺寸相对于波浪长度较小时莫瑞斯方程才有效，也就是说，D＜0.2L，而且只适用于非阻断波。在深水区，如果H/L超过0.14，波浪会发生阻断。

惯性系数取决于结构横截面形状和方位。典型的，C_M的范围在1.6～2.5之间。对于垂直圆柱体，C_M=2.0。对于带有海洋生物粗糙度的圆柱体，由于海洋生物的生长，C_M通常不小于1.8。阻力系数C_D不小于0.6，对于光滑圆柱，C_D=1.0。惯性力和阻力的相对幅度如图4-23所示。

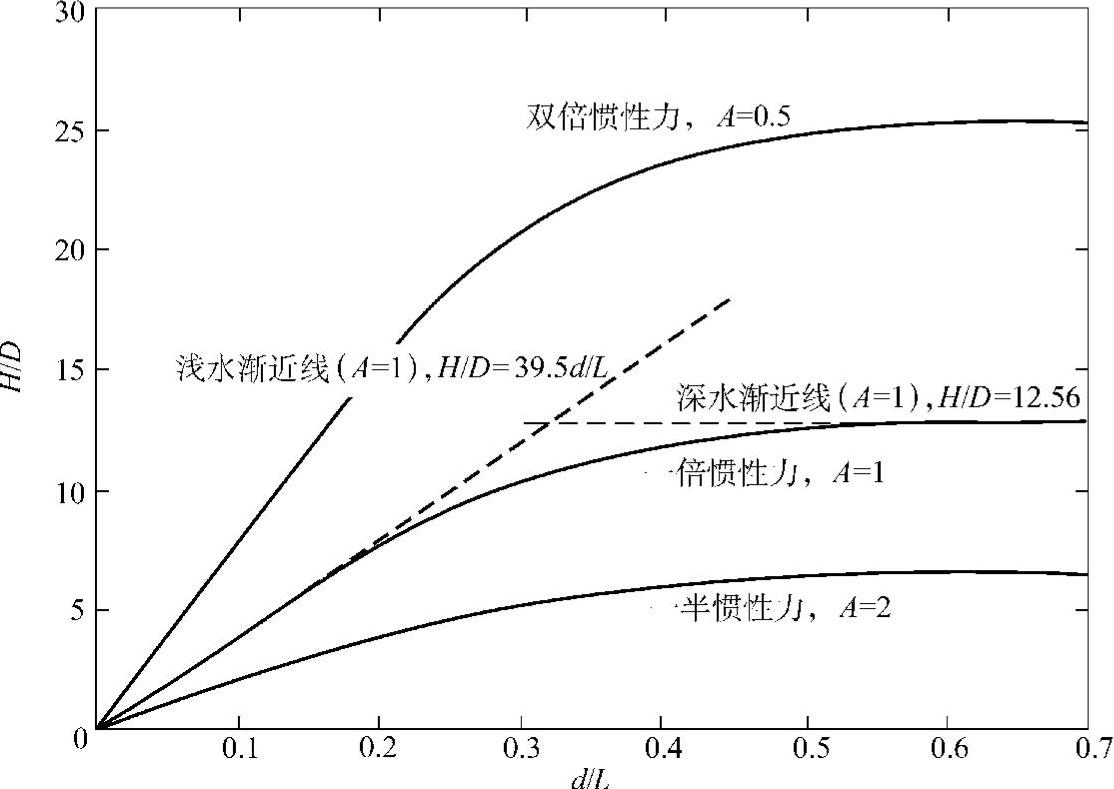
图4-23 惯性力和阻力的相对幅度

图4-24给出了水深10m处一个直径为4m的圆柱体利用莫瑞斯方程计算的例子。其上部分图给出了海面变化过程，中间部分图给出了在静水水面情况下，水微团的水平速度和加速度，下部分图给出了海床处的水平波浪力和倾覆力矩。此例基于C_M=2和C_D=1.2。

惯性力可以表示为

F_M=A_Mcos（ωt）

阻力为

F_D=A_Dsin（ωt）|sin（ωt）|

式中 A_M——惯性力的幅值；

A_D——阻力的幅值。

令A表示两个幅值之比，即A=A_M/A_D，可以建立以下的关系：

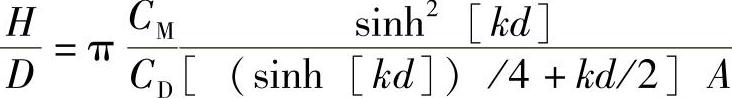
这种关系可以表示为图4-23所示。对于给定结构和位置，只要计算比值H/D和d/L，就可以利用图4-23快速得知惯性力或阻力中哪一个是主要的。

参照图4-23，对于位于A=1曲线上方的结构，试验载荷其阻力项在莫瑞斯方程中占主要部分。而对于位于A=1曲线下方的结构，惯性载荷占主要部分。图4-23中的两条渐进虚线分别对于浅水波浪（d/L＜1/20）和深水波浪（d/L＞0.5）有效。渐进线是从小幅值波浪运动学的渐进结果导出的。

例如，在丹麦海域Middelgrunden和R∅dsand场址，一个直径D=5m的圆柱体承受波浪气候。两个场址在各种工况下，对应不同比值H/D、d/L和A的水深及波浪数据见表4-9。在两个场址A都出现，这表明惯性力是主要载荷。

表4 - 9 惯性力与阻力之间的比值

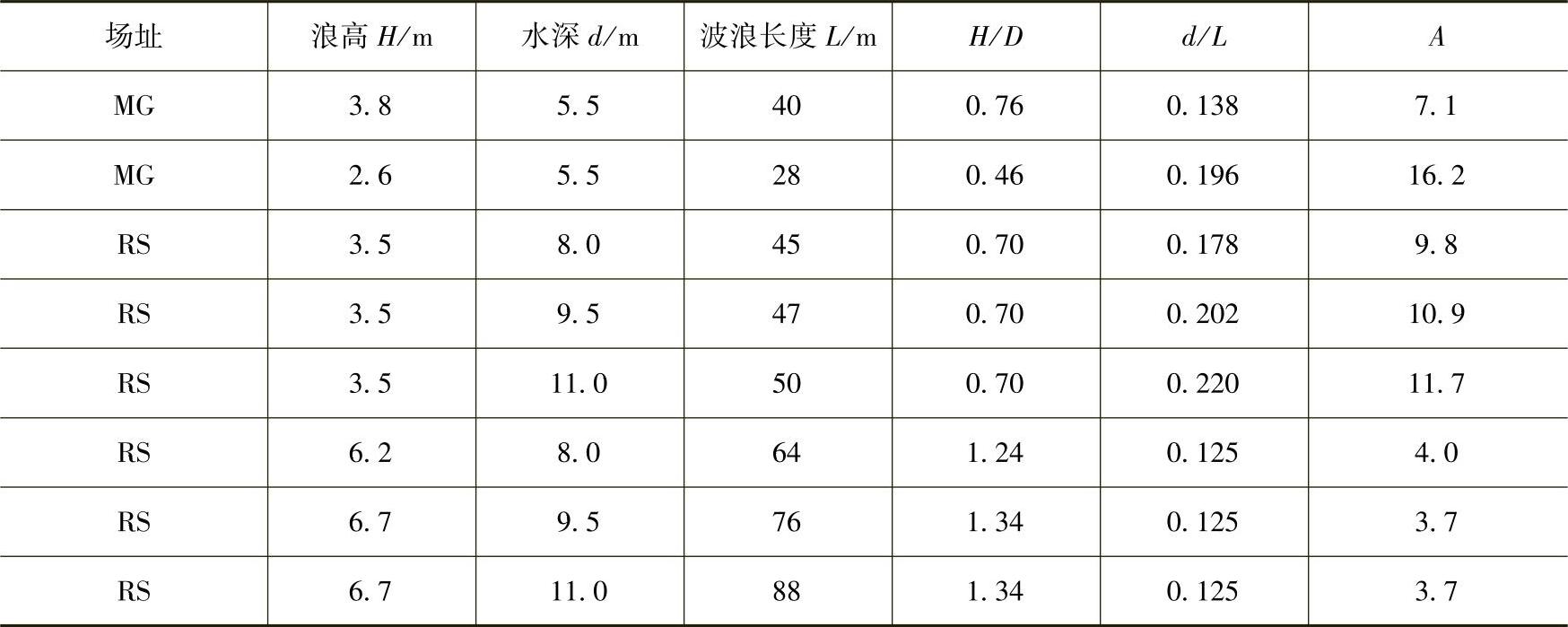
注：1.MG代表Middelgrunden场址。

2.RS代表R∅dsand场址。

6.根据衍射理论计算波浪力

如果结构的尺寸与波浪长度相比较大，如D＞0.2L，此时莫瑞斯方程不再有效，惯性力将是主要的，并且可以通过衍射理论进行预测。对于水深d处，半径R=D/2的圆柱体，承受幅值为A的波浪，衍射理论给出的最大水平波浪力为

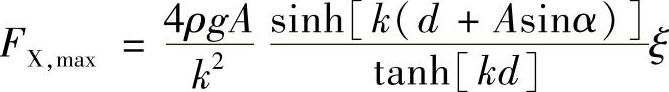
从海底计算的垂直力臂为

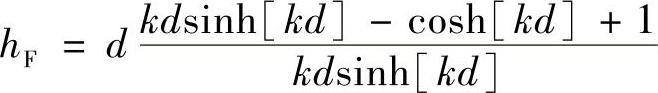
系数ξ和α在表4-10给出，引自Gran（1992）相关研究文献。

上述方法可以用来预测圆柱状基础结构的波浪力，如单桩和重力基础结构。注意，如果结构的几何形状偏离假设的圆柱体过大，上述公式可能导致完全错误的结果，如在浪涌区放置一个锥形结构部件来吸收或减小冰载的情况。

另外也要注意，在浅水区当波浪通过倾斜的海床时，波浪可能发生阻断。因此，如果这些波浪足够大，就有可能破坏前面方程的动力学假设。对于水平海床，由于太大的波浪在达到特定地点前波浪已经破断了，因此局部阻断就不必考虑了。这些波浪在到达指定地点前，波浪的高度将遵从由水深给定的极限，在它们到达制定地点前，又将符合假定的波浪动力学假设。

波浪载荷严格取决于水深。鉴于此，考虑当地水深的变化，包括天文潮汐和暴风巨涌是十分重要的。