特殊考虑：结构阻尼对风力发电机的影响与扭转振动的特性分析

1.结构阻尼

为了通过气弹分析程序分析得到真实的响应，必须小心地对结构阻尼作出规定。结构阻尼模型包括在运动方程中，以确保结构系统中的能量耗散。如果所有的模态都可以测量，通常只需对有限几个模态形状进行测量就可以得到结构阻尼。

经验显示，对数衰减形式的结构阻尼对叶片通常量级是3%，而对主轴和塔架通常为5%。针对19m风轮叶片对数衰减的例子见表4-3（Baumgart等人，2000）。为了确保能量耗散，要求运动方程中源于结构阻尼的阻尼矩阵部分C是正定的或至少是半正定的，即

x^TCx≥0

结构阻尼矩阵的正定确保了在所有速度下的能量耗散。

表4-3 19m叶片模态阻尼的对数衰减率

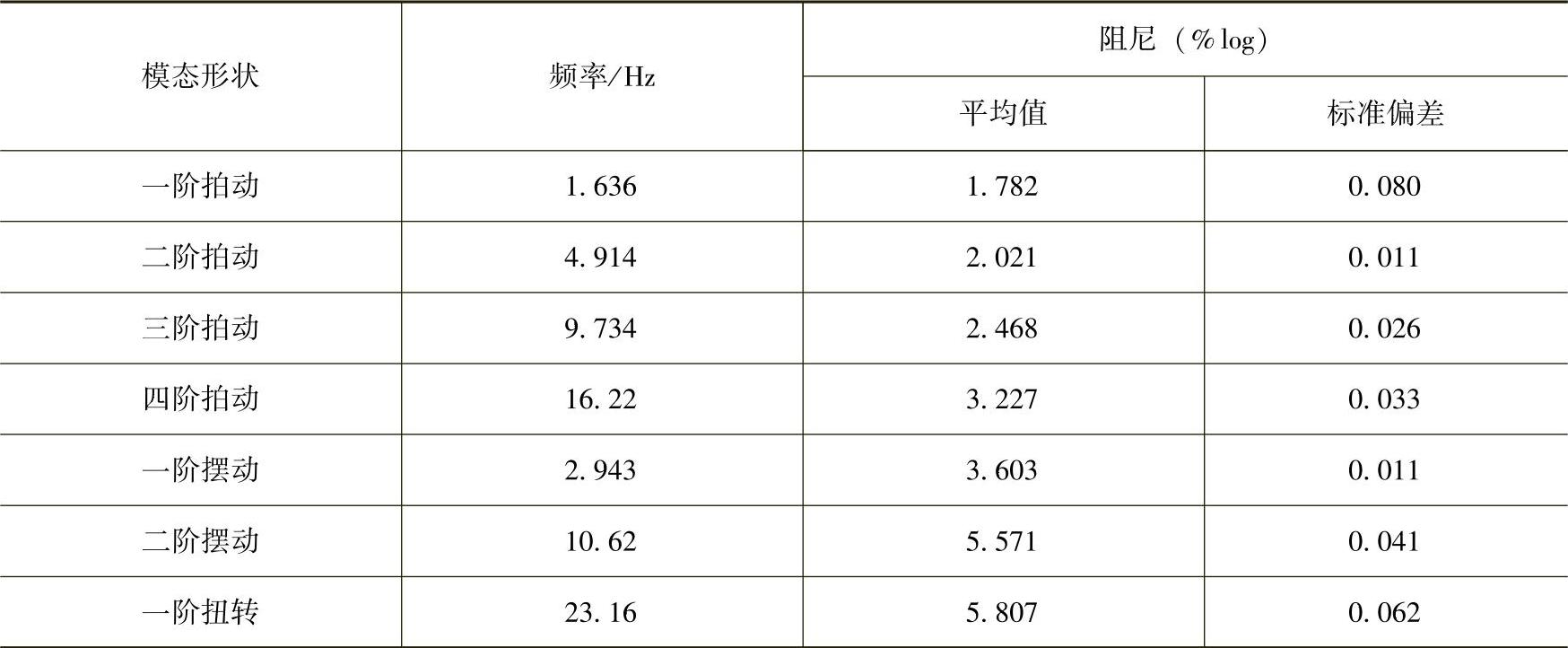
最常见的阻尼模型表达式是瑞利（Rayleigh）阻尼模型。它的主要优点是只要采用模态公式，运动方程就是解耦的。阻尼模型的形式是

C=αM+βK

式中 C——阻尼矩阵；

M——质量矩阵；

K——刚度矩阵；

α，β——模型常数。

参考资料见Bathe（1982）相关研究。瑞利阻尼模型仅精确拟合了两个测量的阻尼比。此处α、β通过两个阻尼比率决定，它们分别对应于不同的振动频率。

使用瑞利模型的缺点是对高频振动阻尼的预测偏大。

对于更通用的阻尼模型，假定阻尼比p已经确定。基于这一点，阻尼矩阵用考伊级数（Caughey series）表示，即

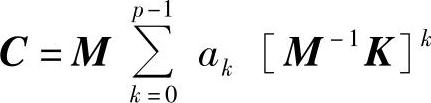
式中 C——阻尼矩阵；

M——质量矩阵；

K——刚度矩阵；

p——阻尼比的数量；

a_k——模型常数。

模型常数a_k可从p的联立方程（simutaneous equations）得到，即

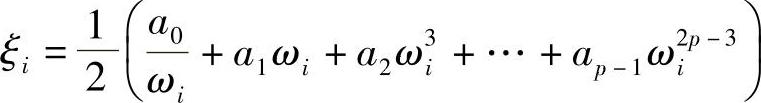
式中 i——i=（1，p）；

ξ_i——第i阶阻尼比；

ω_i——振动模态的角频率。

使用通用阻尼模型的缺点是，在一般情况下，阻尼矩阵C是一个满秩矩阵。这样就导致在气弹分析仿真中变得非常耗费时间。对于p=2，通用模型退化为瑞利阻尼模型。

为了正确评价这里所表示的结果，回顾第i阶阻尼比定义为

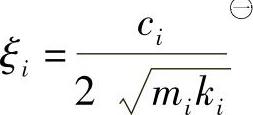
㊀ 原书有误，错将c_i写为了c。——译者注

式中 m_i——第i个质量；

c_i——第i个阻尼；

k_i——第i个刚度。

相应的对数衰减量为

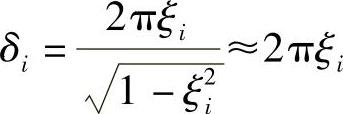
这个对数衰减量是幅值衰减率的自然对数，如在两个连续的位移循环中幅值比率的自然对数。

2.结构阻尼的确认

如果在气弹模型中，阻尼系数选用了一些初始估计，那么必须确认模型产生了正确的阻

尼表达式。这可以通过固定风力机所有的自由度而只保留要检查阻尼模型的一个自由度来实现。在所考查的结构部件（如叶片）上施加一个外部的周期性力，使用部件的固有频率作为激励频率，结构只激励几秒钟，然后测量诱导振动的衰减，则阻尼系数就很容易通过方程的拟合曲线得到，即

f（x）=Cexp（-δf_nt）

式中 t——时间；

f_n——激励频率；

δ——对数衰减率；

C——来自拟合的校正常数。

这样一个拟合例子如图4-10所示。模型中的动力系数必须调整直至从试验中得到正确的对数衰减率δ。

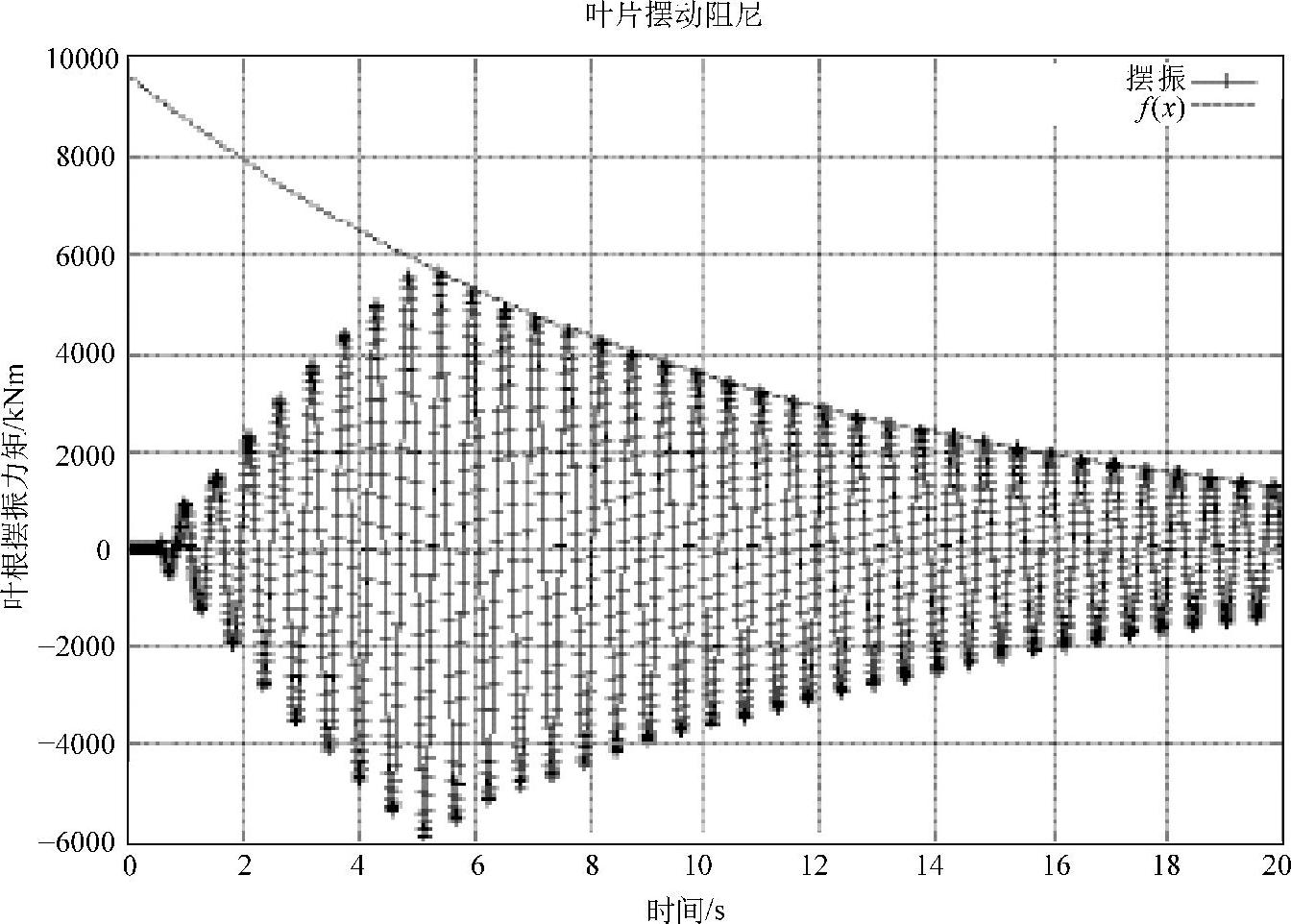
图4-10 风轮叶片摆振阻尼试验(www.xing528.com)

只有采用瑞利阻尼模型，才可能仅通过两个频率拟合出正确的阻尼特性。如果阻尼特性在更多的频率上是已知的，如表4-3中的例子，就只能选择几个阻尼的平均代表值。在本节中，重要的是要注意采用瑞利模型在高频时会对阻尼的预测偏高，如对玻璃纤维材料上高频冲击力的分析。

3.叶片失速诱导振动

风力机中存在这样的情况，即出现了大幅度的叶片摆动方向的振动，即使是在相对中等风速状态，用10min平均风速来描述大约是15m/s时，叶片会产生大幅度的摆动方向振动。这样的摆动方向振动从结构观点来看是不希望出现的，需要避免。一旦负的气动阻尼超过结构阻尼，摆动就会发生。气动力为振动提供的能量多于结构阻尼所能吸收的能量。图4-11和图4-12给出了对500kW风力机进行仿真得到的这样一个振动的例子。图4-11给出了在基本构造下的振动，而图4-12给出了在新构造下主轴刚度增加的振动。两图均引自Petersen等人（1998）的相关研究。注意，挥舞方向的振动同样重要，需要加以考虑。

摆动有问题时，关于新叶片设计和旧叶片改造方面的建议由Petersen等人（1998）给出，这里重复一下。

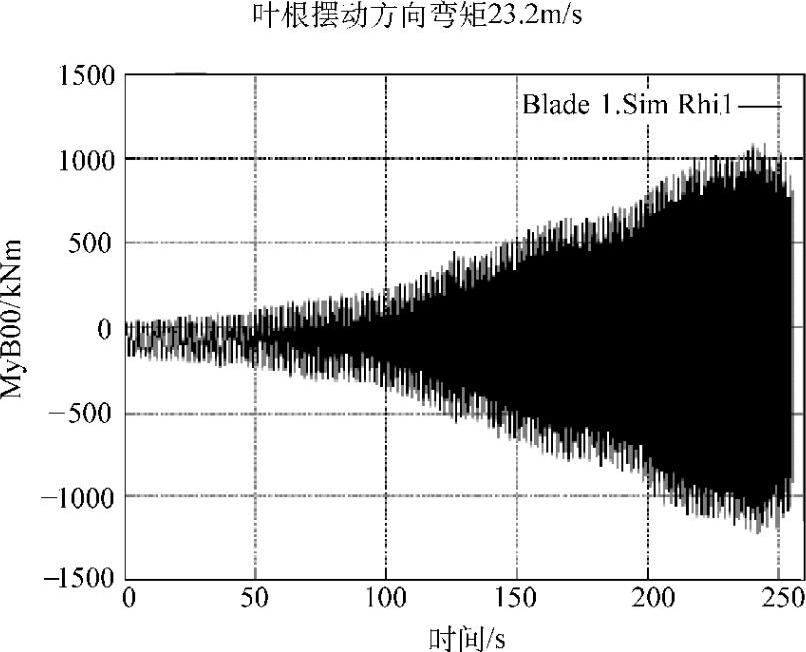
图4-11 基本构造500kW风力机叶根处摆动方向力矩

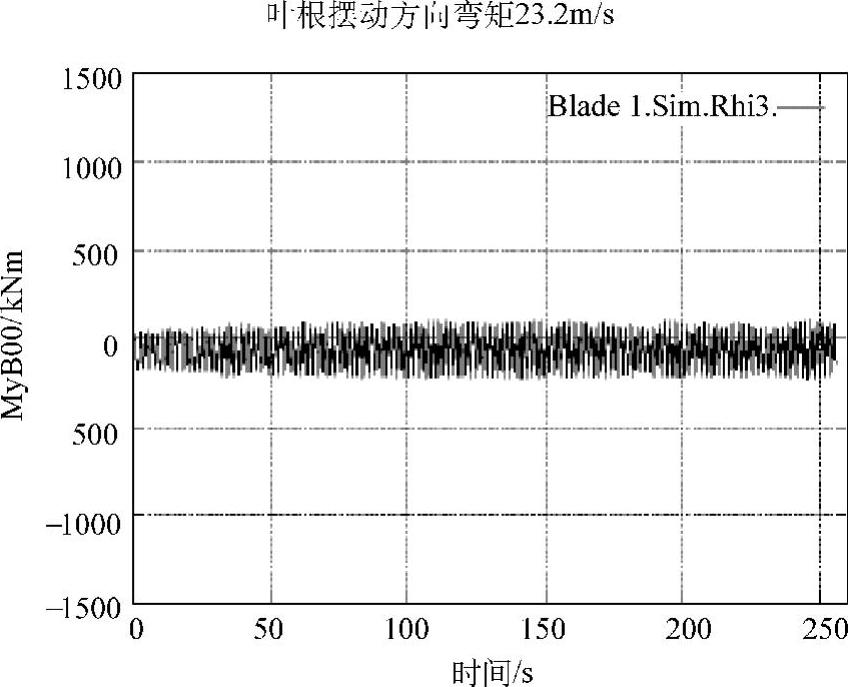
图4-12 主轴刚度增加的500kW风力机叶根处摆动方向力矩

对于新设计风力机，此时拥有很多的自由度，建议按下述的程序进行：

1）翼型数据齐全的基本翼型。

2）选择翼型。叶片的外形（弦长、气动扭转）以及叶片的结构特性（刚度、质量、模态形状，如变形的幅值和方向、结构阻尼、模态质量、模态刚度及模态固有频率），不仅要考虑风轮的性能，而且要考虑气动阻尼特性。特别地，应该考虑叶片扭转，它不仅与功率特性有关，而且与振动方向模态形状有关。

3）运用准静态方法（Petersen等人，1998）计算单只叶片的基本气动阻尼特性，考虑基本的挥舞和摆动模态形状。如果不满意，则重复步骤2），反复进行。

4）扩展准静态分析，包括对模型进行叶型升力和阻力两个方面动力失速的验证，此时仍只考虑单独的一只叶片，如果不满足，重复步骤2）。

5）如果单只叶片的分析得到了恰当的气动阻尼，则用全气弹模型继续进行分析，包括确定模型在翼型升力和阻力两方面的失速滞后。结构模型必须对叶片的弯曲模态以及风轮的旋转模态有足够详细的描述。

6）对所感兴趣的风速进行全气弹计算，通过单只叶片分析可以在很大范围的风速上进行确认。

7）通过对叶片在挥舞和摆动两个方向固有频率上的响应进行观察，从而对阻尼特性进行研究，如基于叶根弯距的功率谱密度。

8）如果结果不满意，重复步骤2）。

如果某一台特定风力机，在挥舞振动和摆动振动方面存在问题，那么该风力机必须进行改进设计，此时只有有限的几种可能性被保留。

1）一般对已有的设计应使用上述步骤。

2）叶片的气动特性可以通过使用不同的气动装置得到改进，如采用失速条（或涡流发生器）。

3）风力机的结构特性可以通过增加局部质量或增加局部刚度特性的方法来改变，这些变化能以希望的方式改变模态形状和固有频率。

4）机械阻尼装置可以用在叶片或支撑结构上。应该提醒的是这些装置并没有消除振动的根源，振动是由气动力提供能量的。

4.颤振

颤振是一种气弹不稳定性，它可能导致很大幅度的振动，甚至可能导致失效。颤振由叶片的挥舞振动和扭转振动的耦合组成，它是由叶片周围的气流来维持的。颤振要发生，必须有几种不利的条件存在。其中两个最关键的条件是：一是挥舞方向弯曲模态频率与一阶扭转模态频率之间没有足够的分离；二是叶片横截面的质心位于叶片截面气动中心的后面。气动中心通常近似地在弦长的1/4处，如图4-4距进气边c/4距离处。因此设计叶片时，重要的是确保高的扭转刚度（如一阶扭转频率比一阶挥舞频率大10倍）。在应用上，确保叶片横截面的质量中心位于进气边和1/4弦长点之间。

5.失速条和涡流发生器的使用

失速条可以用在风轮叶片的外侧区域（典型的是在外侧1/3部分），当叶片发生剧烈振动时，用作一种“紧急”动作。一般地，失速条通过失速增加阻力来增加叶片局部区域的阻尼。

涡流发生器通常用于增加升力从而改进叶片的气动性能。涡流发生器用于叶片的内侧区域，从而改善这一区域的最大升力，带失速条和涡流发生器改进的例子如图4-13～图4-16所示（Petersen等人，1998）。

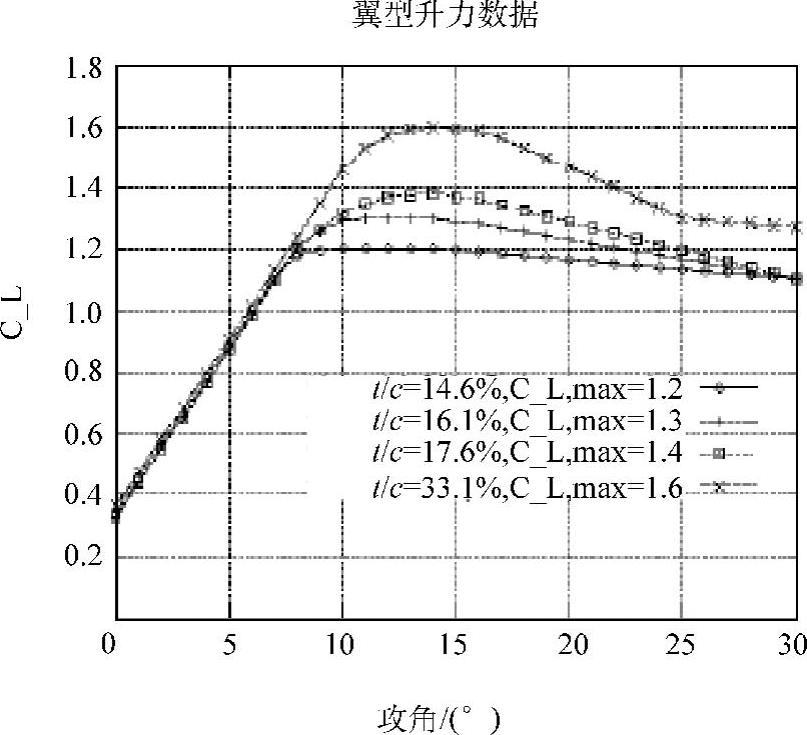
图4-13 翼型升力数据（未改进）

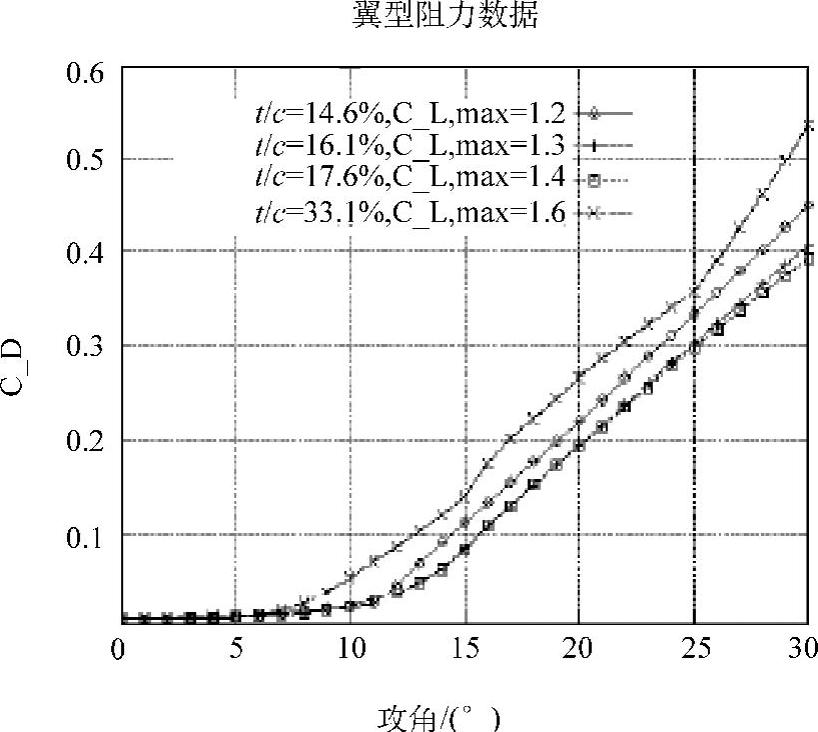
图4-14 翼型阻力数据（未改进）

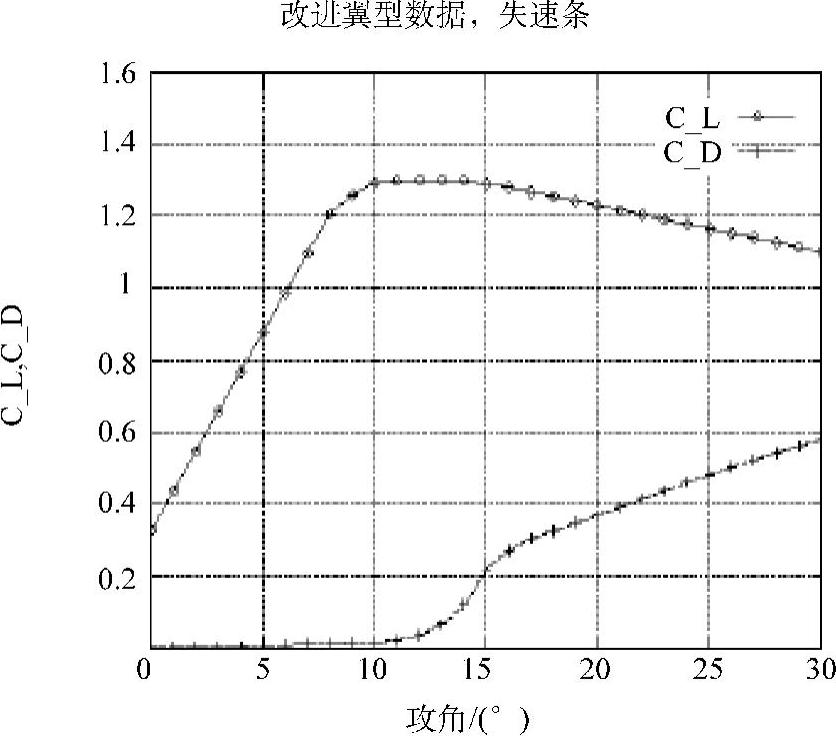
图4-15 带失速条的翼型数据

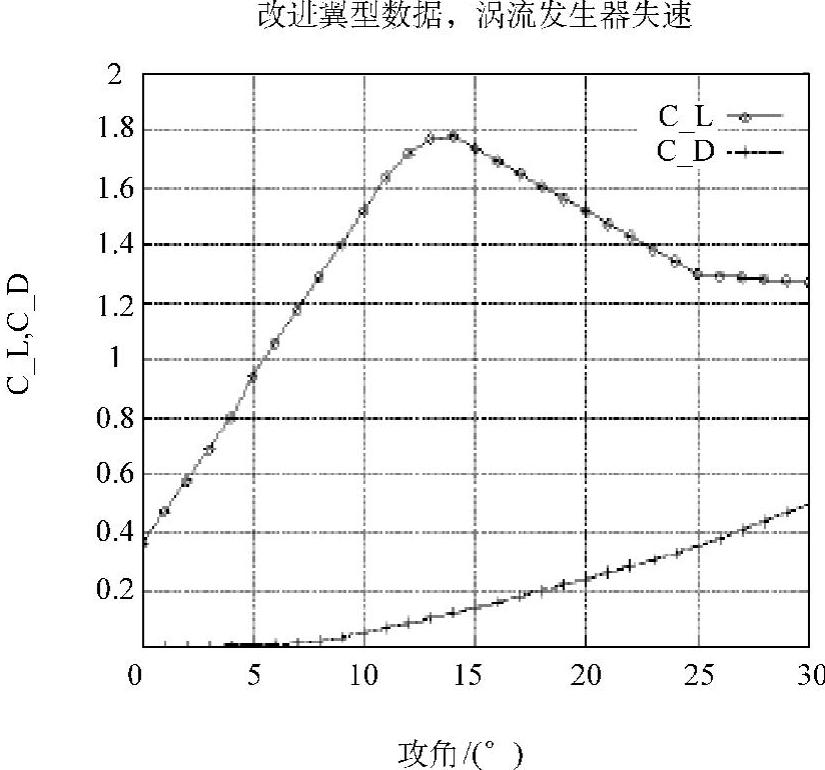
图4-16 带涡流发生器的翼型数据

6.动力失速

如果入流角周期性变化，那么失速的起始就会延迟，如入流角按如下计算：

α（t）=α₀+βsin（ωt）

式中 α₀——名义入流角；

β——幅值；

t——时间；

ω——角频率。

失速起始被延迟的现象被称为动力失速，它影响升力和阻力系数。当发生失速延迟时，考虑动力失速是重要的，因为升力和阻力系数是以恒定进流角的风洞试验导出的。各种动力失速模型可以在Petersen等人（1998）的相关研究文献中找到。

在风洞中测量的β=2°的动力失速例子如图4-17所示。

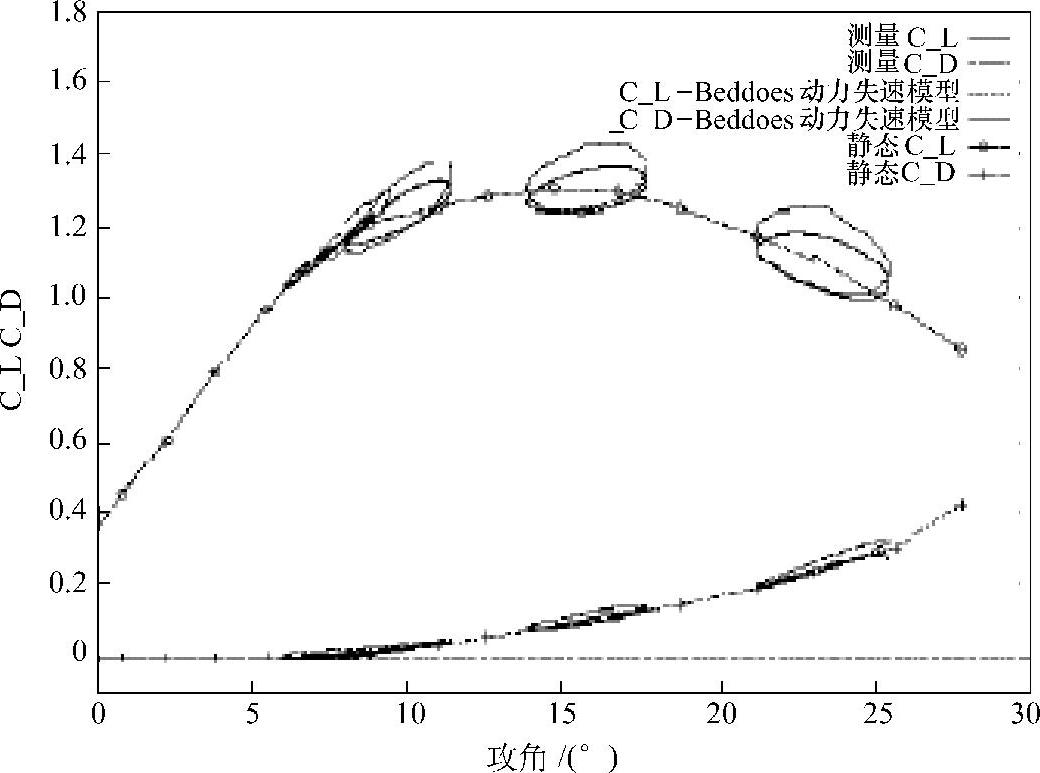
图4-17 C_L和C_D回路动力失速