风切变：对小型风力机的影响及稳定修正示例

风切变理解成风速随高度的变化。对于小型风力机，如风轮直径为10m等级的风力机来说，风切变并不是很重要。对于大型或柔性风轮来说，风切变可能就是十分重要的了。很多失效都是由风切变在叶片上诱导的载荷引起的。

风廓线很大程度上取决于空气的稳定条件。如图3-6所示的例子，即使在24h之内，风廓线也会在白天和黑夜、黎明和黄昏之间变化。

风切变廓线可以根据3.1.1节提出的对数模型通过稳定修正导出，这个经稳定修正的对数风切变模型为

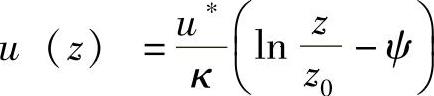
式中 ψ——稳定性函数，非稳定条件时它的值为正，稳定条件时它的值为负，而处于中性条件时它的值为零。

不稳定条件常常出现在表面受热和垂直混合增加的时候，稳定条件常常出现在表面冷却（如夜晚）和垂直混合受到抑制的时候。图3-7给出了一个特定位置各种条件下经稳定修正的对数风切变廓线例子。

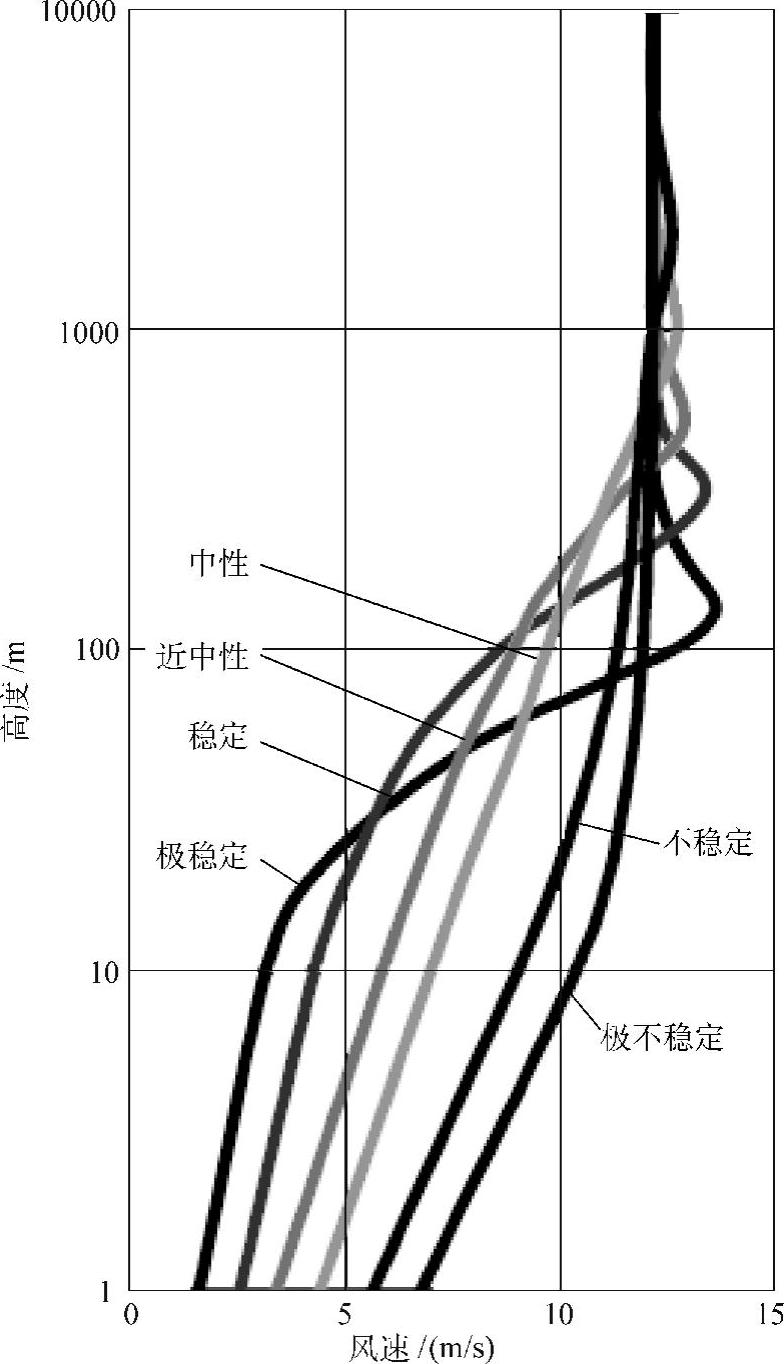
图3-6 各种稳定条件下的风切变廓线（粗糙度z₀=0.02m，自转风速G=12m/s）

图3-7 中性、稳定及不稳定条件下的风廓线

稳定性函数ψ取决于无量纲稳定性度量，即ζ=z/L_MO，z是高度，L_MO是莫林-欧波霍夫（Monin-Obukhov）长度。稳定性函数可以通过下式来计算：

式中 x——x=（1-19.3ζ）^1/4。

莫林-欧波霍夫长度L_MO是由热流量和摩擦速度u^*决定的，它的值反映了机械力和热力对湍流的相对影响。表3-2给出了莫林-欧波霍夫长度L_MO的典型值。

表3-2 莫林-欧波霍夫长度L_MO的典型值

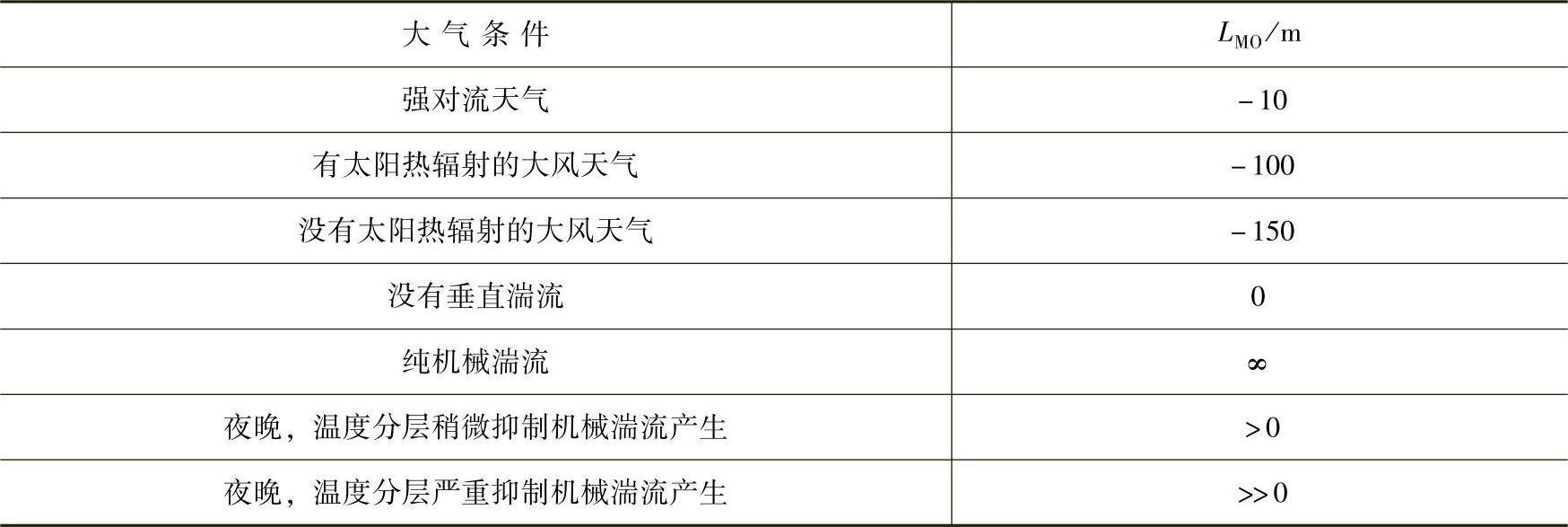
如果有理查森（Richardson）数R的数据，则可以通过下面的经验关系求得莫林-欧波霍夫长度L_MO：

(www.xing528.com)

如果没有数据，理查森数可以通过平均条件计算，即

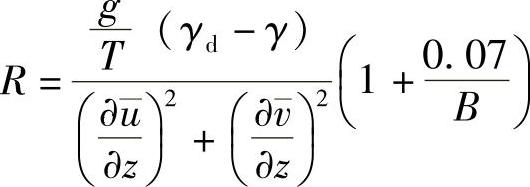
式中 g——重力加速度；

T——温度；

γ——γ=-∂T/∂z，下降速率；

γ_d——γ_d≈9.8°C/km，干绝热下降速率；

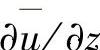和——两个水平平均风速分量u和v的垂直梯度；

z——垂直高度；

B——靠近地表面对潜在热流量敏感的鲍文（Bowen）比近似为

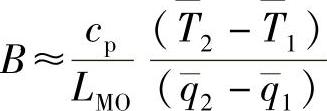
式中 c_p——比热；

L_MO——莫林-欧波霍夫长度；

和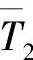——1和2两个高度水平上的平均温度；

和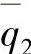——同样高度水平上的平均比湿度。比湿度q是湿度与质量的比值，请参考Panofsky和Dutton（1984）的相关研究。

地形特征，如山丘、山脊和悬崖等都会影响风速。在这些地形特征附近，一些气流层会加速，风廓线会改变。计算这种变化的风廓线的理论见Jensen（1999）的相关研究。图3-8给出了一个受山脊影响的例子。

图3-8 在一个二维山脊的上风向和山顶、山脚下风向观察的风廓线