短路电流热效应Qd的计算方法优化

短路全电流为

因而

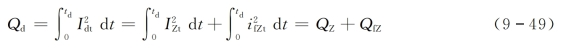
式中　IZt——对应时间t的短路电流周期分量有效值，kA；

ifZt——短路电流非周期分量起始值，kA；

QZ——短路电流周期分量热效应，kA2·s；

QfZ——短路电流非周期分量热效应，kA2·s。

1.短路电流周期分量热效应QZ的计算

图9-6是计算短路电流周期分量热效应的图示。短路电流周期分量的热效应，就是0至短路持续时间td区间内曲线下的面积。采用近似的数值积分法，即可求出短路电流周期分量热效应QZ为

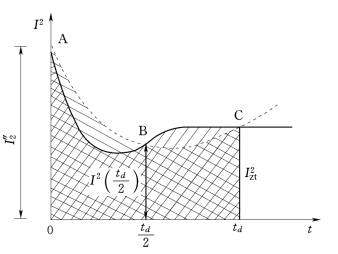
图9-6　短路电流周期分量热效应的图示

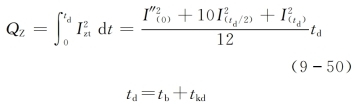
式中　I"（0）——次暂态短路电流周期分量有效值；

I（td/2）——td/2时刻短路电流周期分量有效值；

I（td）——td时刻短路电流周期分量有效值；

td——短路电流持续时间；

tb——继电保护动作时间；

tkd——断路器全分闸时间。

当为多支路向短路点提供短路电流时，I"（0）、I（td/2）、I（td）分别为各支路短路电流之和。

2.短路电流非周期分量的热效应QfZ的计算

图9-7是计算短路电流非周期分量热效应QfZ的图示。短路电流非周期分量的热效应QfZ，就是求0至td区间内曲线下的面积。根据短路电流计算的基本原理，。因而

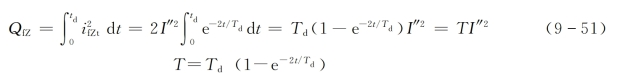
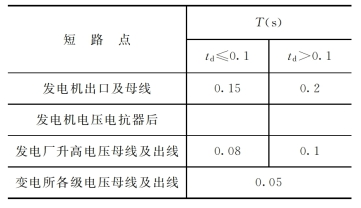
式中　T——非周期分量等效时间，它的大小决定于Td及td。

为了简化计算，可以从表9-9中查取不同情况的T值。

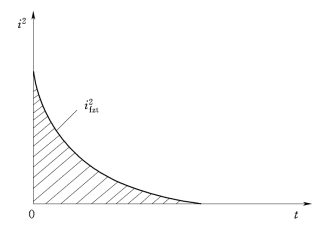
图9-7　短路电流非周期分量热效应的图示

表9-9　非周期分量等效时间T　单位：s

(www.xing528.com)

【例9-2】发电机出口的短路电流I"（0）=16kA，I（0.5）=8.2kA，I（1）=7.1kA，短路电流持续时间td=1.5（s），试求短路电流热效应。

解　短路电流周期分量热效应

短路电流非周期分量热效应

短路电流热效应

3.导体短时最高温度θd的计算

热平衡方程式（9-47）可改写为

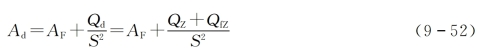
当已知导体材料和导体正常发热温度θF时，可按图9-5查出相应的AF值。然后加上短路电流的热效应，即可求出Ad值，最后再由图9-5的曲线查出Ad对应的导体短时最高温度θd。

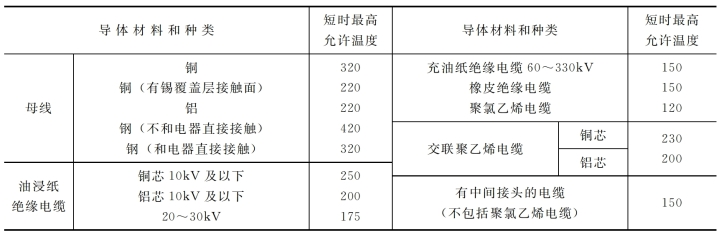
所求得的短时最高温度θd应小于或等于导体短时最高允许温度，才能满足导体短路热稳定要求。导体的短时最高允许温度列于表9-10中。

表9-10　导体的短时最高允许温度θd.N单位：℃

4.导体最小允许截面Smin的计算

为了简化计算，也可用计算导体最小允许截面Smin的方法来校验导体的热稳定。为此，可假定短路前导体的温度已达正常工作最高允许温度θN，而切断短路时导体的温度恰好达到短时允许最高温度θd.N，这时对应的导体截面即为满足热稳定条件的最小允许截面Smin。

根据θN及θd.N查出相应的AN及Ad，然后代入式（9-47）中，可得

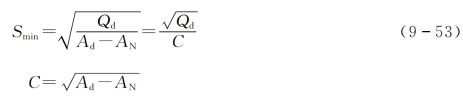
式中　C——常数，可从表9-11中查取。

只要导体的截面S≥Smin，导体即满足热稳定要求。

表9-11　裸导体决定Smin的C值

【例9-3】截面为150×10-6m2的10kV铝芯纸绝缘电缆，正常运行时温度θF为50℃，短路电流热效应为165.8kA2·s，试校验该电缆能否满足热稳定要求。

解　由图9-5查得AF=0.38×1016（A2·s/m4）

由图9-5查得θd=150C＜θd.N=200C，该电缆是热稳定的。

另外，由表9-11中查得C=97×106

由于电缆截面S=150×10-6m2＞Smin=132.7×10-6m2，所以用最小允许截面法校验导体的热稳定满足要求。