【摘要】：载流导体短时发热的特点是：发热时间很短，发出的热量来不及向周围介质散布，因此散失的热量可以不计，基本上是一个绝热过程。将式、式、式代入式，即得导体短时发热的微分方程整理后得对式进行积分，当时间由0到td，导体温度由开始温度θF升到最高温度θd，于是式左端的与短路电流产生的热量成正比，称为短路电流的热效应，用Qd表示。
载流导体短时发热的特点是：发热时间很短，发出的热量来不及向周围介质散布，因此散失的热量可以不计，基本上是一个绝热过程。即导体产生的热量，全都用于使导体温度升高。又因载流导体短路前后温度变化很大，电阻和比热容也随温度而变，故也不能作为常数对待。
在导体短时发热过程中热量平衡关系是，电阻损耗产生的热量应等于升高温度所需的热量，可表示为
在时间dt内，式（9-38）可写成
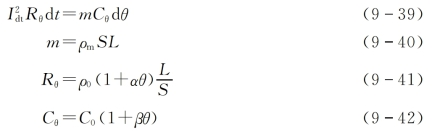
式中 Idt——短路全电流有效值，A；
Rθ——温度为θ℃时导体的电阻，Ω；
Cθ——温度为θ℃时导体的比热容，J/（kg·℃）；
m——导体的质量，kg；
ρ0——0℃时导体的电阻率，Ω·m；
α——ρ0的温度系数，℃-1；
C0——0℃时导体的比热容，J/（kg·℃）；
β——Cθ的温度系数，℃-1；
L——导体的长度，m；
S——导体的截面积，m2；(www.xing528.com)
ρm——导体材料的密度，kg/m3。
将式（9-40）、式（9-41）、式（9-42）代入式（9-39），即得导体短时发热的微分方程
整理后得
对式（9-44）进行积分，当时间由0到td（td为短路切除时间），导体温度由开始温度θF升到最高温度θd，于是
式（9-45）左端的
与短路电流产生的热量成正比，称为短路电流的热效应，用Qd表示。式（9-45）右端为导体吸热后温度的变化，积分得
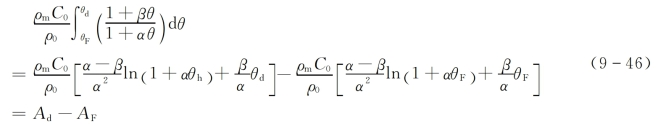
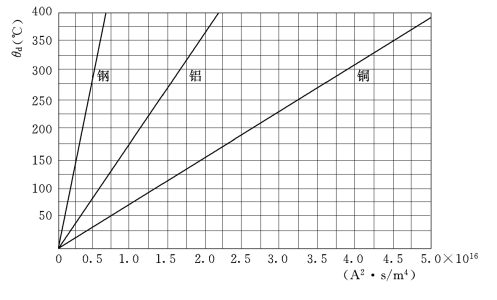
图9-5 铜、铝、钢三种材料的θ=f（A）曲线
Ad与AF值与导体材料和温度有关，铜、铝和钢的θ=f（A）如图9-5所示。当已知导体温度θ时，可方便地求出A值；反之，由A值也可求出导体温度θ。
这样，式（9-45）可写成
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
