疲劳载荷与S-N曲线解析

S-N曲线，也称为沃勒（Wöhler)曲线，用来描述使材料或构件疲劳破坏的循环次数N与应力幅值S的关系。通过多个样品实验，测试不同应力幅值范围S和该范围内的疲劳破坏循环次数N，可以测得S-N曲线。

S-N曲线通常可以表达为^[116]

其对数形式为线性关系:

式中 K——材料的经验常数，决定着S-N曲线的高低；

m——沃勒指数，表征S-N曲线的坡度。

对数形式的S-N曲线如图14-3所示。其中，S_E为疲劳极限（endurance limit)；S_D为应力常值下的疲劳极限（fatigue limit)；S_B通常为极限强度（ultimate strength)。(www.xing528.com)

根据S-N曲线，给定一定的应力幅值范围，就可以确定疲劳破坏应力循环次数。图14-3中的线性关系分为两段，在钢材中普遍使用。在疲劳极限S_E以下不会发生破坏是钢材和钛合金的一个特性。S-N曲线是材料的特性，不同材料差别可能很大。

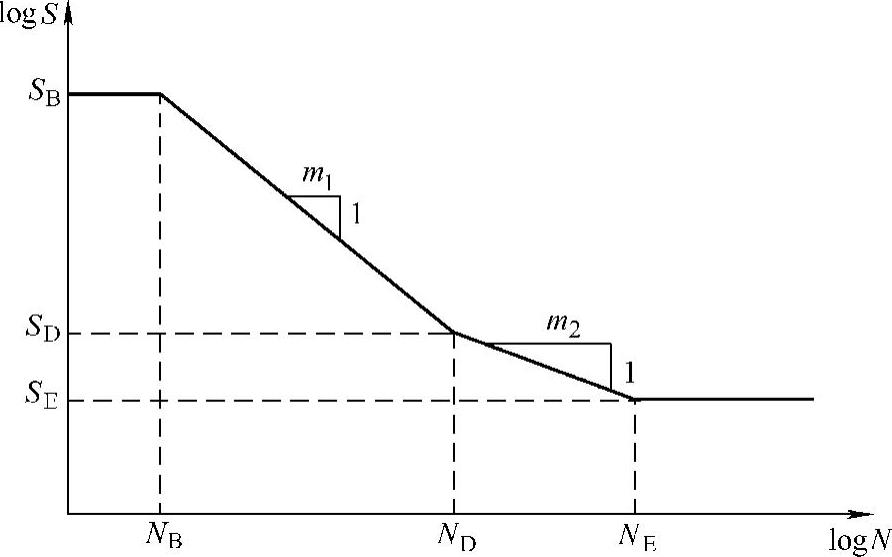
图14-3 S-N曲线^[116]

可以用折铁丝的简单实验理解S-N曲线。用双手弯折一段铁丝，经过几次弯折后，铁丝就会被折断。那么，到铁丝被折断为止，弯折的次数为应力循环周期，弯折的幅度可以理解为应力的大小。显然弯折的幅度越大，折断所需的弯折次数越少。如果给定弯折的速度和幅度，就很容易推算经过多长时间铁丝会被折断，即材料的寿命。

破坏应力循环次数可以轻易地转换成材料的使用寿命。风力发电机的设计寿命通常为20年，可以反推出对应力载荷的承受能力。材料的破坏应力循环次数LogN会发生自然的波动，通常用标准偏差σ表示。通常平均S-N曲线为50%的超越概率下的特定情形。在风力发电机的设计中，必须采用保守的方式，S-N曲线的超越概率通常为97%～98%。

疲劳载荷是周期性载荷，对结构部件的材料造成累积损伤，并最终导致结构破坏。疲劳载荷通常远低于造成静态破坏的载荷水平，需要多次载荷循环才会发生疲劳故障。这种情况通常是指高周期疲劳（简称高周疲劳)。但对于某些材料，尤其是S-N曲线坡度陡峭的材料，如一些环氧树脂材料，重要的疲劳载荷则接近造成静态破坏的载荷。对于这些材料，疲劳载荷变成极值形式，仅需少量应力循环周期就可以导致疲劳破坏，通常称为低周疲劳。