【摘要】:动叶片的惯性和重力载荷与质量有关。重力的表达式为[116]式中 g=9.82m/s2,为重力加速度;m——叶片的总质量。尤其当风力发电机偏航时,就会产生回转载荷,且不论结构是否有弹性(或柔性)都会发生。很多情况下,可以忽略回转力矩效应,因为偏航角速度通常非常小。但是,弹性的轮毂支撑会产生显著的回转力矩(旋转涡),同时兆瓦级的风力发电机也不能对其进行忽略。图14-1 叶片截面上的气流速率[116]
动叶片的惯性和重力载荷与质量有关。叶轮面的离心力Fc与角速度、半径位置和每个叶片元的质量有关。
把叶片分解为n个有限的叶片元,则在叶片根部,离心力为[116]:

式中 mi——第i个叶片元的质量;
ω——角速度;
ri——第i个叶片元的半径位置。
重力的表达式为[116]

式中 g=9.82m/s2,为重力加速度;
m——叶片的总质量。
通常,任何弹性的旋转支撑都会产生回转载荷。尤其当风力发电机偏航时,就会产生回转载荷,且不论结构是否有弹性(或柔性)都会发生。因此风力发电机偏航时会在垂直轴线周围产生偏航力矩MK和在水平轴线附近产生倾斜力矩MG。
对于三叶片的叶轮,有回转力矩产生的偏航力矩的合力矩为零,即MK=0,而倾斜力矩MG不为零,有:(https://www.xing528.com)

式中 ω——叶轮旋转的角速度;
ωK——偏航角速度;
对于两叶片的叶轮,回转力矩将导致周期性变化的偏航力矩和倾斜力矩:
MK=2M0cosωtsinωt
MG=2M0cos2ωt (14-4)
以上表达式需要就叶轮面的倾角进行调整。
很多情况下,可以忽略回转力矩效应,因为偏航角速度通常非常小。但是,弹性的轮毂支撑会产生显著的回转力矩(旋转涡),同时兆瓦级的风力发电机也不能对其进行忽略。
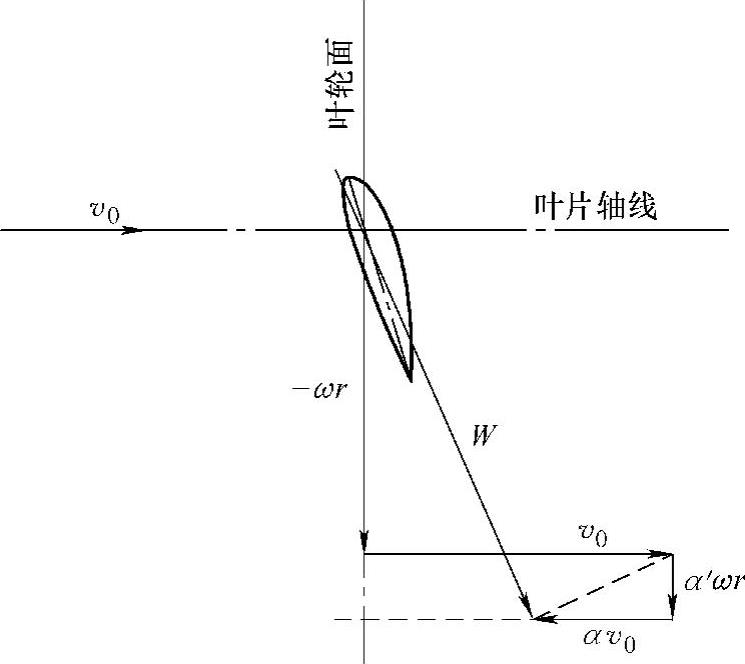
图14-1 叶片截面上的气流速率[116]
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




