机舱风速和自由风速的关联性

丹麦理工大学Risø实验室^[114]和美国国家可再生能源实验室^[113]通过对具体项目的研究，得出了几乎相同的结论，本小节就将这些基本结论展现给读者。

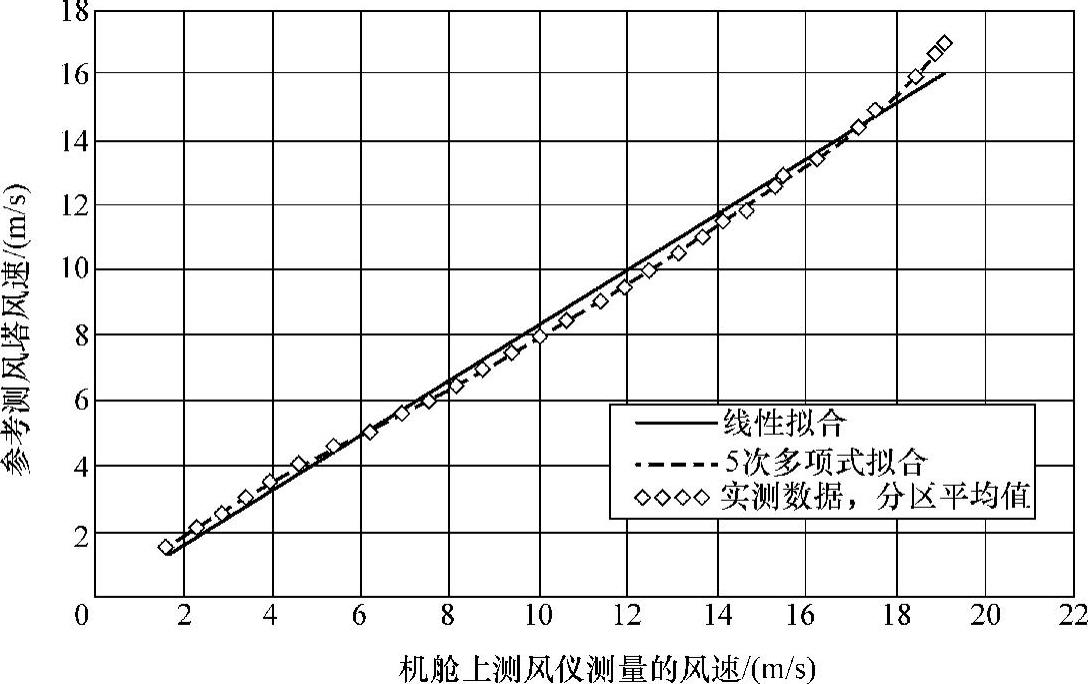
图13-8 机舱风速与测风塔风速的关系[114]

图13-8为风力发电机组（变桨距角)机舱上风速仪测量的风速与自由风速的关系，其中参考测风塔风速可以代表自由风速，测量扇区的选择是根据IEC 64100-12进行的。

可见，从切入风速到15m/s之间，两者有较好的线性关系。当风速超过15m/s时，线性度下降。这可能是由于当风速超过15m/s时，风力发电机组满发，风轮转速不再随着风速变化而变化，能量转化系数迅速下降。机舱风速仪的非线性特性，使得线性回归法明显高估了6m/s～11m/s风速段的风速约3%，低于4m/s和高于16m/s的风速段则被低估了至少3%。这一特点导致线性回归的标准误差较大，回归曲线常数的不确定度较高。Risø实验室的研究成果还表明，虽然不同风速段的线性度有所不同，但是机舱风速与自由风速之间的总体线性相关度非常高。图13-8的线性相关系数R高达0.99467。(www.xing528.com)

在整个风速区间上，5次多项式回归能更好地拟合机舱风速与自由风速之间的关系，回归曲线的标准误差也小得多。但是由于回归曲线的参数个数多（6个)，单回归系数的统计不确定性很大^[114]。

Risø实验室的报告认为，修正机舱风速仪更好的方法是对每个数据域分别求修正系数。每个数据域的修正参数为该数据域内的测风塔风速与机舱风速之比的平均值。然后，将这些修正参数应用于机舱风速仪测量的每个10min平均风速值。对于多数数据域来说，修正后的机舱风速与测风塔风速差别小于1%，且没有像线性回归那样的系统性错误。数据域修正法的标准误差小于0.1m/s，各数据域的平均误差小于1%。当风速高于4m/s时，修正后的机舱风速与测风塔风速之差的标准误差（可视作该方法修正10min平均的机舱风速的不确定度)为2%～3%。

用机舱风速仪评估功率曲线时，每个数据域的样本数越多，修正的统计不确定性越小，且理论上收敛于测风塔风速与修正后的机舱风速之差的平均值。

总体来说，因为自由风速与机舱风速之间有良好的相关性，把机舱风速用于风力发电机组功率曲线的验证是有可能的。修正机舱风速方法的选择，最好基于修正后的机舱风速和测风塔风速之间的统计学比较。修正方法的选取标准可能是，在最重要的风速区间内（如4～16m/s)，标准误差小于0.1m/s。