中尺度气象模型的不确定性分析

理论上，可以通过中尺度模型对任何风场的风况进行模拟。因此中尺度气象模型在风资源评估领域的应用也越来越受到重视。市场上，已经出现了一些中尺度模型的商业软件，且价格不菲。

然而，中尺度模型却是一把双刃剑，因为我们往往高估了计算机模型的能力。和其他数值模型一样，中尺度气象模型也存在巨大的不确定性。不了解这些不确定性，而盲目依赖中尺度模型会导致严重的决策错误。

对于天气预报来说，气象模型已经很先进，预测水平基本满足日常生活需要。退一步讲，如果天气预报不准，比如预测下雨却没下或预测下午下雨结果半夜才下等，其后果一般是可以承受的，因此我们可以不必在意。然而预测风机发电量对预报结果的精确度要求要出高几个数量级。不要忘了，风机的发电量约与平均风速的三次方成正比。

对于风资源工程师来说，可能不必亲自用超级计算机对中尺度气象模型进行建模和计算，但必须清楚中尺度模型的不确定性，及其适用范围和应用方法。毕竟中尺度气象模型是帮助我们降低风资源评估的不确定性的。

首先计算机仅能计算离散数，因此必须把大气分割成数量有限的体积单元（有限元)，并用计算节点代表。计算节点就是节点，是体现全部气象变量值的地方。显然，对连续场进行离散描述的精确度取决于计算节点的密度，也就是模型的分辨率。然而中尺度气候模型的分辨率不可能过高，否则会降低模型稳定性，反而失真。

一般来说，中尺度气候模型的分辨率不宜超过1km。低于1km属于微观选址的范畴，必须使用专门的计算模型。

同时，我们还必须把这些连续的微分方程离散化后才能用数值计算方法解析。在用离散的空间和差分方程表达连续场的微分方程时，误差不可避免。

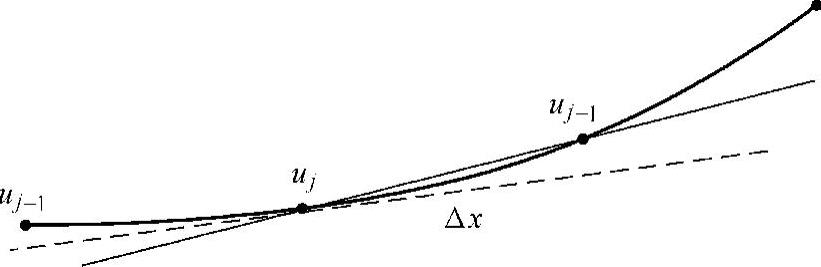
图11-32 对连续曲线进行有限差分和离散化

除了离散误差和有限差分误差外（见图11-32)，数值计算过程中还必然存在截断误差。由于实际运算只能完成有限项或有限步运算，因此要将有些需用极限或无穷过程进行的运算有限化，对无穷过程进行截断，这样产生的误差称为截断误差。例如，求一个级数的和或无穷序列的极限时，我们取有限项作为它们的近似，从而产生了误差，这种误差称为截断误差。

例如下述有限差分和离散化过程，很好地解释了离散误差和截断误差:

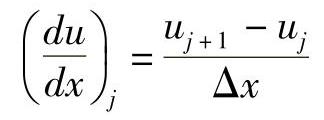（有限差分和离散化，左侧表达的虚线)

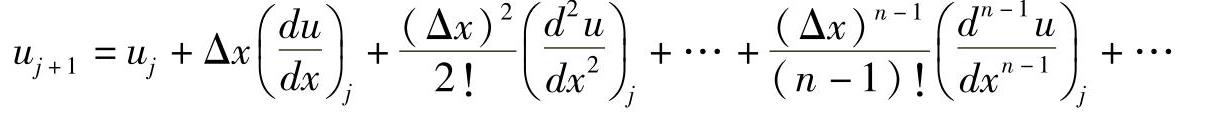
另

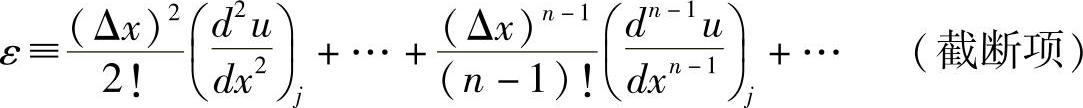(www.xing528.com)

则

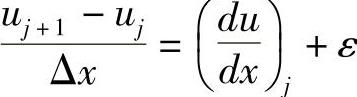
除了已知的离散误差和截断误差外，还存在其他误差。这些误差来源于方程组的不完整性、为了提高计算效率和系统稳定性而忽略掉的已知物理过程，以及已知变量的未知影响和大气中未知的物理过程。

而对于湍流的描述因其涵盖非常宽泛的空间尺度而无法完全模拟，即使用最先进最昂贵的气象和其他流体力学模型也做不到。然而湍流对风力发电至关重要。

美国气象学家爱德华•罗伦兹（Edward N.Lorentz)1963年在一篇提交纽约科学院的论文中分析了这个效应。一个气象学家提及，如果这个理论被证明正确，一只海鸥扇动翅膀足以永远改变天气变化。在以后的演讲和论文中他用了更加有诗意的蝴蝶。对于这个效应最常见的阐述是:“一只南美洲亚马逊河流域热带雨林中的蝴蝶，偶尔扇动几下翅膀，可以在两周以后引起美国德克萨斯州的一场龙卷风。”其原因就是蝴蝶扇动翅膀的运动，导致其身边的空气系统发生变化，并产生微弱的气流，而微弱的气流的产生又会引起四周空气或其他系统产生相应的变化，由此引起一个连锁反应，最终导致其他系统的极端变化，如图11-33。它称之为混沌学。

天气系统作为极其复杂的和非线性的系统，任何一个微小的误差都可能是一只蝴蝶的翅膀！

图11-33 蝴蝶效应

因此在把中尺度数值模拟的风数据应用于风资源与微观选址时，要格外小心，否则可能适得其反。基本原则是中尺度数值模拟生成的风数据不能直接用于风电场发电量评估，必须与实际测风数据拟合对比后才能判断是否可用。也就是说，中尺度气象模型不能替代测风塔。即使是在风场开发密度高且地形简单的情况下，也需要用周围风场的实际发电数据进行对比分析。

不同的中尺度气象模型生成的数据与实际测风数据的拟合度是不一样的，同一个中尺度气象模型生成的不同地点的数据与实际测风数据的拟合度也可能是不一样的。

如图11-34所示，中尺度数值模拟的风数据与实际的测风数据的总体变化趋势是相近的，即可以预见二者的拟合度是比较高的，但是平均风速与实际相差却很大。可近似理解为中尺度数值模拟的风数据的相对值是准确的，而绝对值是不准确的。然而这是比较好的情况，有很多情况就连趋势也相差很大，那么这种数据是不能用的。因此模拟数据的可用与否只能通过与实际数据对比分析后才能确定。

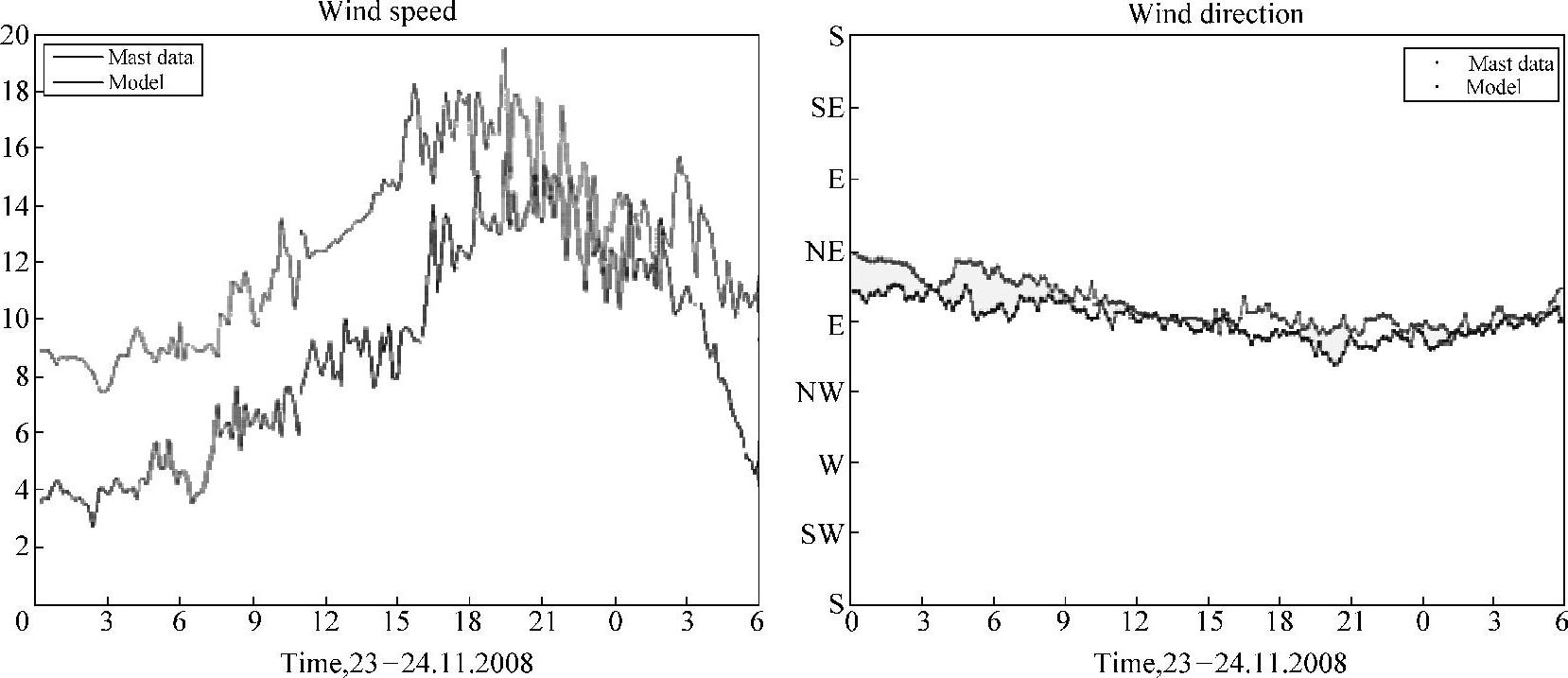
图11-34 中尺度数值模拟风数据与实际测风数据对比

当然，随着技术的发展，计算能力的提高和经验的积累，中尺度天气模型的模拟数据会越来越接近实际，但还有很长的路要走。