压力梯度、力和风：探究气象力学中的基本概念

风使空气中的能量进行了再分配。当两个点之间的距离无限小时，它们之间的压力差就变成了局部特性，称作压力梯度:

任何流体内的压力梯度都将产生一个力，来试图重建平衡，即对物质进行再分配使压力梯度变为0。压力梯度力的大小与空气密度ρ有关。根据定义，任何量的梯度都是矢量，且指向值较高的方向。显然压力梯度力指向压力低的方向，因此用负号表示:

当谈到力时，气象学家总是指单位质量的力，也就是一个空气团的加速度。

当流动的液体受到固体表面限制时，例如地球表面，摩擦力F_F就会出现，阻止液体流动，其方向与运动方向相反。通常，摩擦力的大小与流动速率和距离表面的距离成正比。对于大气来说，复杂之处在于空气中充满湍流，因此对摩擦力的描述包含对湍流通量的描述。

地球是一个旋转的星球，在观测空气流动和气团受力时也需要在一个旋转坐标系统内完成。我们肉眼见到的运动也是由于坐标系统的旋转而导致的合力的结果，我们称之为显力。其中一个分力是用来补偿气团的绝对运动过程，其中包含了气团随着地球表面的运动过程。这个力是由法国物理学家G.G.Coriolis于1835年首先提出的，并以他的名字命名。在北半球，该力使运动物体向右转向，在南半球则正好相反。Coriolis力（也称为科罗拉力或地转偏向力)与运动速度v和Coriolis参数f正线性相关。而Coriolis参数f取决于所在纬度。

式中 ω——地球自转角速度，等于2π/天；

在45°纬度线上，f=10^-4S^-1。由于空气大多不沿着直线运动，而是沿曲线运动，另一个力就出现了，即离心力。离心力把空气推离旋转中心，与速率的二次方成正比，与旋转半径r成反比。也就是说旋转半径越小，力越大。

离心力与向心力紧密相关。当急转弯时，向心力是使汽车保持在路上行驶的真正的力，而离心力却试图把汽车拉进路旁的沟里，如果车轮不能提供足够的向心力，不幸就会发生了。显然对于流体，例如空气，并不能对其施加向心力。

施加在一个气团上的四个力中，仅有压力梯度力不需要运动的存在。因此实际上压力梯度力是大气中导致运动的唯一的力，也就是说它可以把一个空气团相对于周围其他空气团加速。根据牛顿第一运动定律，当施加在物体上的合力不为0时，物体将加速:

(www.xing528.com)

在静态下分析力的平衡是很有帮助，也就是当合力加速度消失时。让我们以最简单和最概括的例子来研究一个空气团的运动过程，即该气团沿直线匀速运动。为了进一步简化，我们假设该空气团距离地面足够高而不受地表摩擦力影响。这是自由大气的情况，即由湍流决定的边界层的上方。受力平衡于是变为:

这两个力达到平衡的过程如图11-1所示。由于压力梯度，空气团被加速而脱离静止状态。由于运动，Coriolis力将出现，垂直于运动方向，并随着运动速度的增加而增加，直到达到最终平衡。最终的风将沿着一条平行于等压线的方向吹动，因为压力梯度力和Coriolis力已经达到平衡而不再加速，这样的风称作地转风（geostrophic wind)。地转风的大小取决于压力梯度、空气密度和该纬度的Coriolis参数:

在典型的情况为:100km空间距离上的压力差为1hPa，在中纬度上，地转风约10m/s。地转风建立的时间尺度为半天到一天。

显然地转风在赤道上达到奇异点，此处f=0。最糟糕的情况下，意味着地转风平衡根本不存在，而必须由其他力来平衡压力梯度力。赤道附近的热带风暴就是主要由压力梯度力和离心力建立的平衡，称作旋转平衡（gyclostrophic balance):

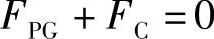
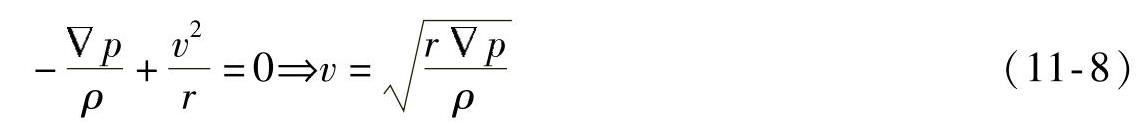
这时的Coriolis参数f很小，可以不计。

当存在摩擦力时，例如存在湍流的低空大气层，就又多出一个力，起到降低风速的作用。在地转风的例子中，Coriolis力将因此不足以平衡压力梯度力，风将向低压侧转向，新的包含摩擦力的平衡将被建立。同样可以应用到旋转平衡的例子。

由于低空大气地表摩擦力的存在，将不能建立匀速直线运动平衡，而发生向低压侧转向。第一种情况转向运动曲线圆心，称为气旋。另一种情况是转离运动曲线圆心，称为反气旋。气旋使空气质量在中心点集中而不得不向上运动，反气旋则正好相反，在中心点形成空心，而必须有上面的空气向下运动进行补充。因此摩擦力是导致空气垂直流动的机制。

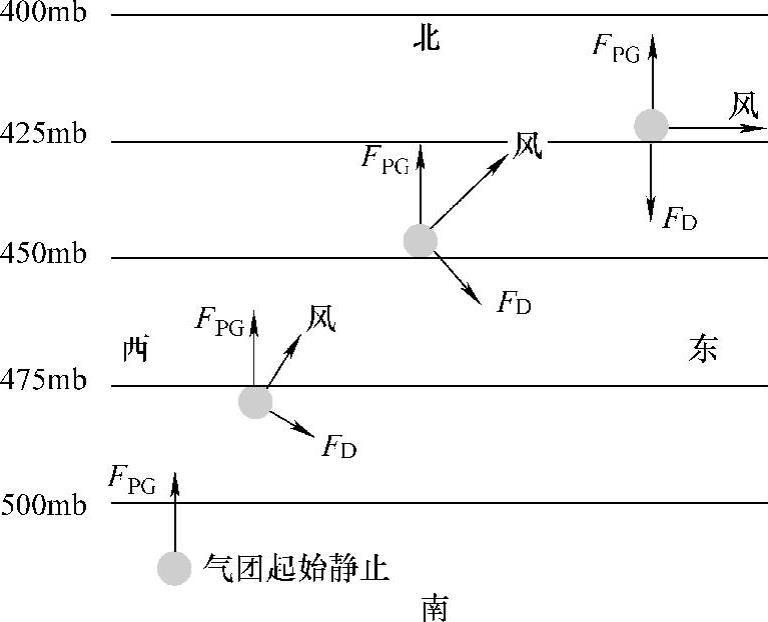
图11-1 地转风在5km高空建立平衡过程，气团起始为静止状态