湍流通量与雷诺平均值的关系

当空间内任意时刻的任意变量不随空间恒定时，运动的空气将通过把周围不同的变量值带过来而改变本地的变量值，称作平流。平流强度与风速、平流变量的梯度和二者之间的夹角有关。冷空气前锋过后本地气温下降就是平流的一个典型例子。分子扩散总是试图在空间内建立各向同性。把墨水滴进清水里的过程是最好的例子。在人类尺度实现单纯的分子扩散是很难的，因为湍流几乎始终存在，哪怕是很弱。

如果没有对湍流过程进行量化的知识是不可能描述边界层的。让我们能够获得这种知识的方法为雷诺平均。雷诺最早提出，可把湍流运动假设成两种运动的组合，在平均运动上叠加了不规则的、尺度范围很广的脉动起伏。用数学方法描述就是任意变量都可分解为平均量和湍流脉动量之和。大气边界层中最常关注的要素有:风矢量的三个分量u、v和w；虚位温θ_v；比湿q以及污染物浓度c等。

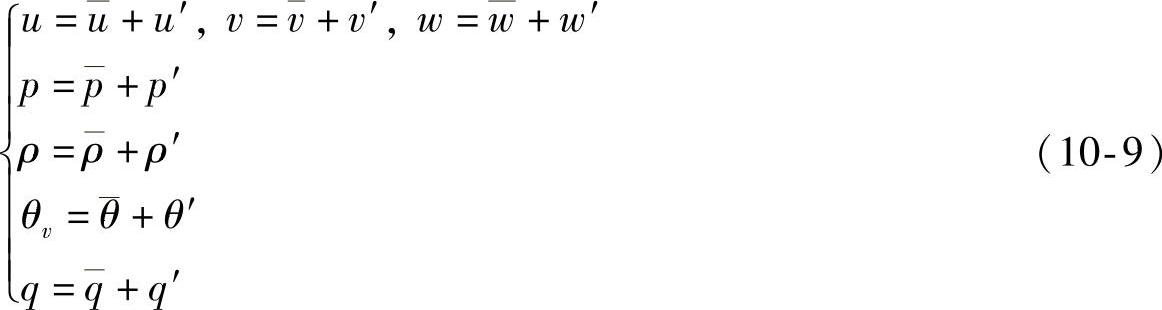
如果我们把坐标系统旋转，使风沿着一个方向流动，那么湍流就可以被看作是二维的，也就是一个垂直切面。水平和垂直分运动可以分解为平均值部分和波动部分:

垂直方向平均风速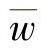显然是0，因为风既不能进入垂直切面也不能在该切面内产生。这是从数学的角度把风分为平均值部分和波动部分，而实际的物理过程（见图10-4)也支持这种做法。

现在对u和w的衍生量取时间平均值并遵循如下规则:(www.xing528.com)

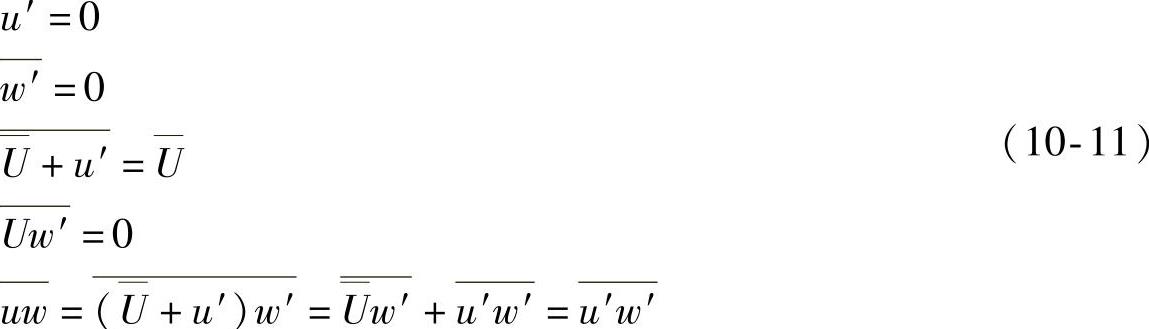
方程（10-11)中最后一项u′w′实际上是二者的协方差。当不等于0时，说明湍流运动的两个分运动方向上的波动不相关，且湍流动量通量将出现在计算结果里。

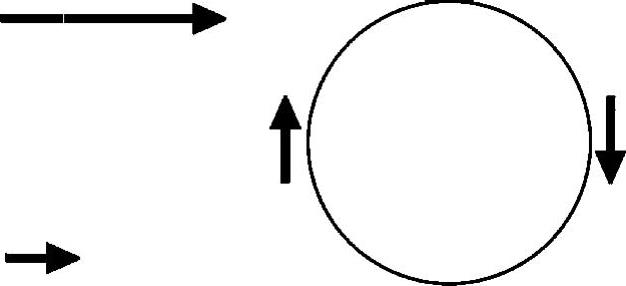
图10-8 垂直方向风速增加和湍流涡旋

如图10-8所示，涡旋的左侧垂直方向的正波动将把一些水平方向负波动带上来，而涡旋的右侧正好相反。所以即使两个方向波动的平均值都为0，它们衍生量的平均值也可以不为0。这个例子中，湍流动量的通量是负的，意味着动量被降低了。我们也可以从这个视角解释为什么湍流的存在增加了风场发电量评估的不确定性。