如何应用泰勒假设测量湍流涡旋的速度？

我们经常需要知道涡旋的尺度和在大气边界层内的运动范围，然而给边界层“拍快照”是很困难的。在大空间尺度范围内的多个地点同时观测是较为困难的，而在同一地点长时间的观测则容易得多。例如固定气象站可以测量边界层变化的时间序列。

泰勒（G.I.Taylor)于1938年提出，在满足某些条件的情况下，当湍流流经传感器时，可以认为湍流是被冻结的。如图10-7所示，一个直径100m的湍流涡旋以10m/s的平均速度平移经过气象传感器。以温度特性为例，在经过传感器初始，左侧温度为5℃，右侧为10℃。经过传感器后，两侧的温度保持不变，因为涡旋是被冻结的。这样就可以把某一固定点测量的气象变量，如温度和风速等，随时间的变化反应成相应的空间分布。需要指出的是，湍流并非是真正冻结的。仅当湍流涡旋发展的时间尺度大于涡旋平流通过传感器所需的时间的情形下，泰勒的简化才适用。

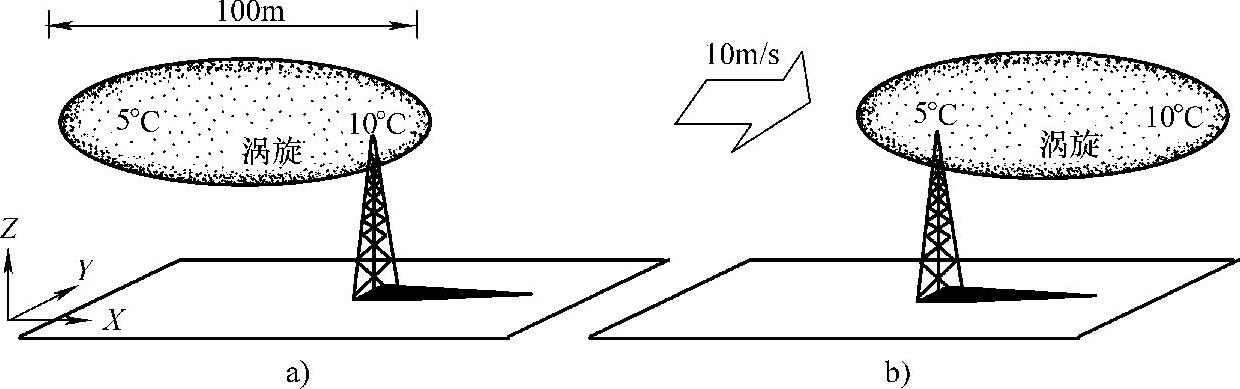
图10-7 泰勒假设^[89]

令U和V代表直角坐标系下两个水平分量的风速，M代表风速的总和，则:

M²=U²+V² （10-4)

若直径为λ的涡旋以平均风速M平移，则通过固定传感器所需的时间为(www.xing528.com)

假设涡旋两侧的温度不同，那么当涡旋通过固定温度传感器时，将测量到温度随时间的变化。根据温度的时间变化特征，就可以对涡旋的尺度进行研究。

为了满足涡旋几乎冻结的假设，Willis和Deardorff（1976)认为

σ_M＜0.5M （10-6)

式中 σ_M——风速的标准差。

因此泰勒假设在湍流强度相对风速很小（＜50%)时是基本成立的。这就提醒我们，湍流不仅可以在本地产生，而且可以从远处平流过来，值得我们在微观选址时予以关注。例如风场位于一大片平地，而远处可视范围内有一些山体，这时就要对山体的形状和与主导风向的关系等进行研究，为微观选址提供指导思路。