经典Gumbel极值分布法优化

通常极值分布方法都使用次序统计方法，即把观测的极值样本排序并重新命名为

其中：

Gumbel法^[68]给每个x_j都赋予一个累计概率F_j，即：

令：

然后对x_j作图（y_j为横轴，x_j为纵轴)，并进行线性回归，如图7-1所示。

由式（7-3)可知，回归曲线应该符合：

等式变换后：

式中 T——风数据的时间长度，单位为年。

线性回归曲线与式（7-17)对比，可以方便地求出Gumbel分布的α和β为两个参数。

于是，1年一遇的极大风速为

50年一遇的极大风速为

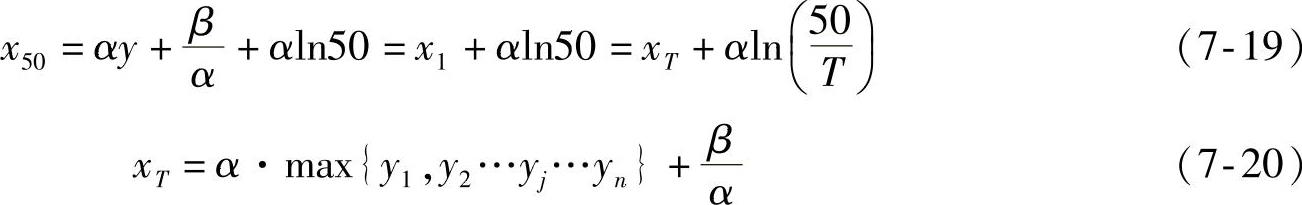
【例】 某测风数据，测风时间为2整年，经从小到大排序后的独立最大风速如表7-2的第1列所示。求50年一遇的极大风速？(www.xing528.com)

对排序后的最大风速进行编号，如表7-2的第2列所示。然后根据式（7-14)求得累计概率F_j如表第3列所示。最后再根据（7-15)求得y_j，如该表第4列所示。

表7-2 某2年测风数据的极大风速计算过程

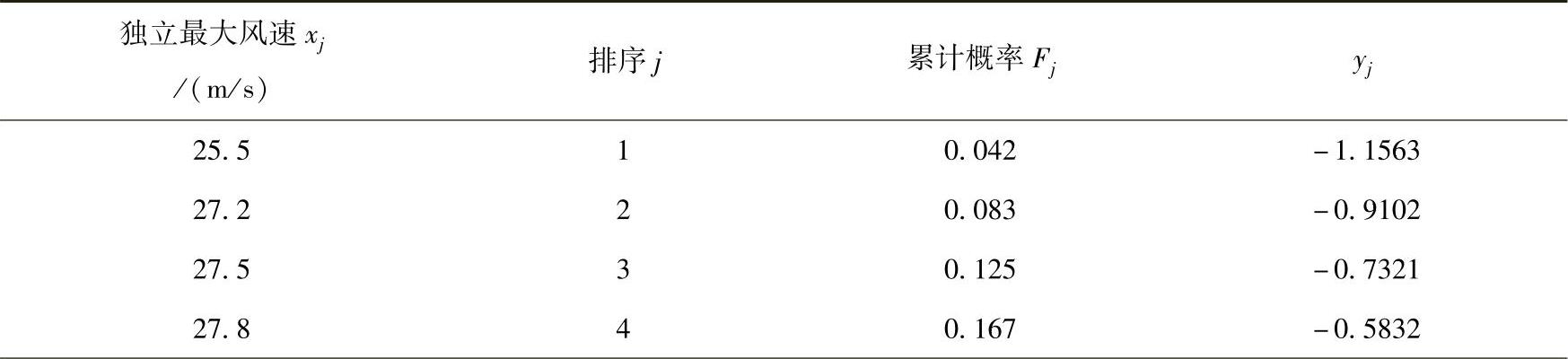
（续)

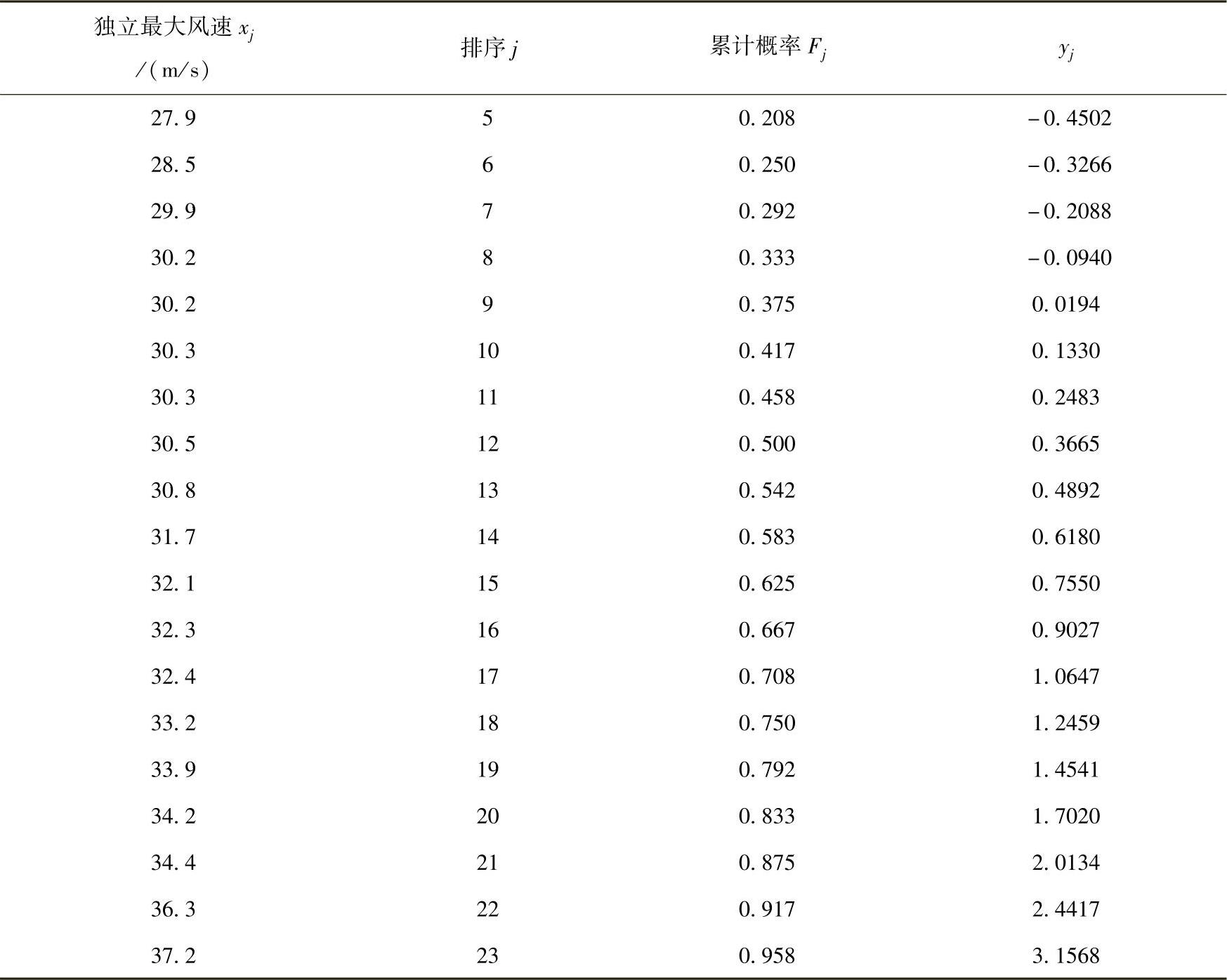
对以表7-2中第4列为横坐标，以第1列为纵坐标，做线性相关，如图7-1所示。根据线性相关拟合曲线可知：

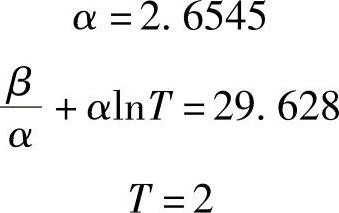
于是可以求得β=73.764；图7-1中的风数据时间长度为2年，根据式（7-20)可知，x₂=38m/s。因此，根据式（7-19)，50年一遇极大风速为

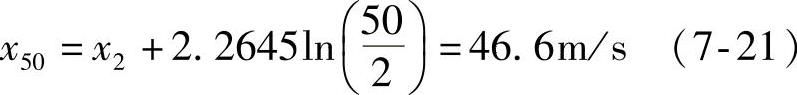
Gumbel法估计的极大风速如图7-2所示，不同再发生周期的极端值分布在线性回归曲线的延长线上。

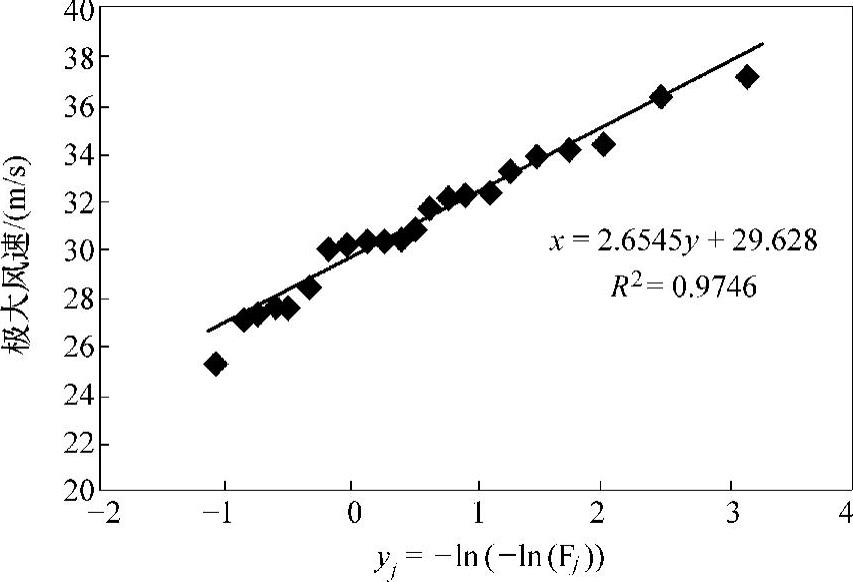
图7-1 风速极值的Gumbel分布拟合

极大风速事件值是基于10min平均的风数据。应通过调整时间窗口和极值下限，将极值样本数量控制在30个以内。需要筛查每个独立的风暴事件是否只有一个极大风速值被计入。一般认为至少4年的测风数据才能获得较好的极大风速估计。

如果极值样本的线性拟合度较差，可以通过删除异常数据点的方式提高拟合度。另外，拟合曲线应尽量与最大的3～5个极值的拟合度最好。

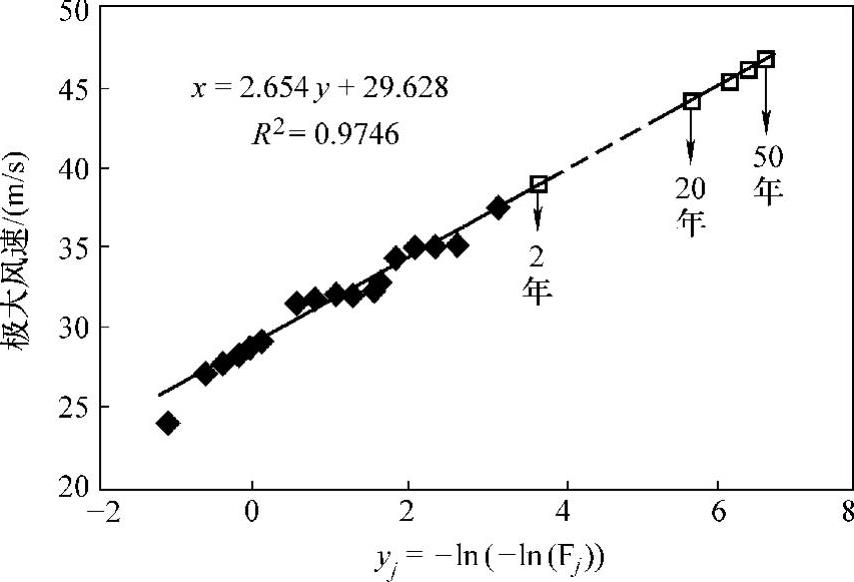
图7-2 Gumbel法估计50年极大风速。空心方块 为估计的不同再发生周期的极大风速值； 实心方块为实测的极端风事件值

极值样本整体可能出现较明显的非线性分布特性，低极值段和高极值段分别依循不同斜率的线性分布。高极值段的斜率可能代表另一个独立的极大风速系统（即潜在的泊松过程)。如台风气候中，台风和普通的风暴就是两个独立的极大风速系统，但在极值样本采集时很难区分开来（即两个不同的泊松过程叠加)。同时，还可能把不是风暴的正常大风采集到极值样本中来，使得极值样本中的低值部分明显不与其他部分成线性关系。

最后需要补充的是，如果测风高度与轮毂高度不同，那么50年一遇的极大风速还须根据风切变换算到轮毂高度。这点在应用气象站的风数据时尤为重要，因为气象站的测风高度往往只有10m左右，与轮毂高度差异较大。