再探数据应用的不确定性

AWS Truewind^[62]对美国全部再分析数据节点进行分析，得到图5-14所示的结论。图5-14中的曲线表明，基于1年的再分析数据预测的10年平均风速的平均绝对误差约为4%；基于8或9年的再分析数据，平均绝对误差降到最低到约2.3%；当超过10年后，平均绝对误差反而逐渐升高。这种现象可能是短期气候波动与长期气候趋势变化的平衡所致。

因此运用NCAR再分析数据作为长期参考数据时，并非越长越好，而是推荐用最近10年的风数据。超过10年可能反而增加了结果的不确定性。

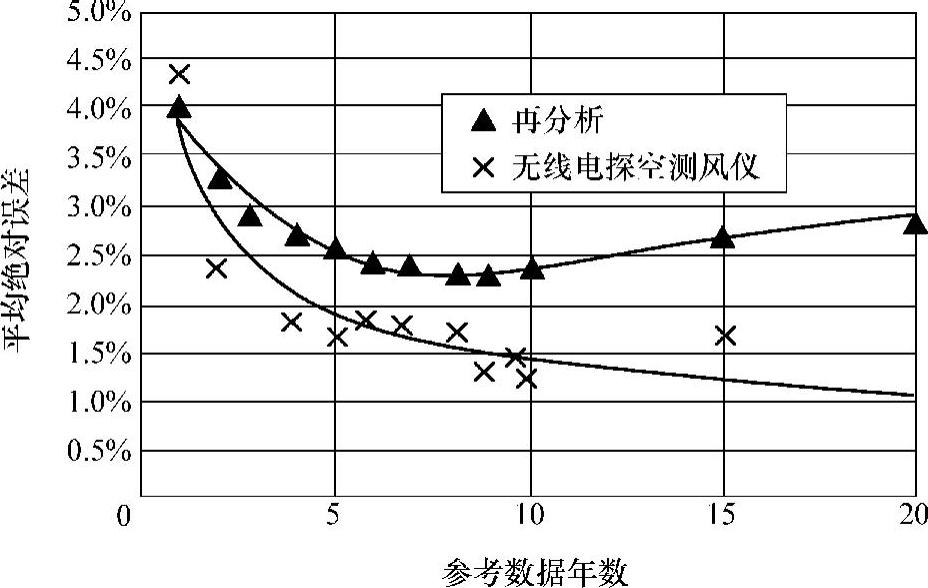
图5-14 预测的10年平均风速的标准误差与再分析参考数据长度的关系，并与无线电探空测风仪站进行对比^[62]

对于无线电探空测风仪数据，其预测的10年平均风速误差则随着参考数据的增加而持续降低，并始终低于再分析数据。这就进一步表明了再分析数据中的一些趋势和变化并非是真实的。

[1]NCEP为美国国家环境预测中心（National Centers for Environmental Prediction)。NCAR全称为美国国家大气研究中心（National Center for Atmospheric Research)。两个机构合作开发的长达50年的气象研究数据的再分析数据，免费共享。数据网格尺寸为2。5°（经度和纬度)，基本覆盖全球。WindPRO2。7提供免费的在线下载服务，数据源网址为：http：∥www。esrl。noaa。gov/psd/data/gridded/data。ncep。reanalysis。surface。html

[2]Bootstrapping在统计学里一般译为自助抽样法。自助抽样法是通过测量采自近似分布的样本的性质来估计一个估计量的性质。近似分布通常是观测样本的经验分布或实际概率分布。假设一组观测样本来自于独立的且遵循同一概率分布的样本空间，然后据此对观测样本进行多次重新采样。例如，测量全世界人的平均身高。我们不可能测量全世界每个人的身高，而仅能对极小部分人进行采样。如果我们对N个人的身高进行采样，那么也仅能获得N个人的一个平均身高值。还需要知道平均值的标准差才能完成表达全世界人的身高分布。(www.xing528.com)

假设任意N个人的身高分布都与以这N个样本的分布一样。这样就可以用电脑生成遵循同一分布的一组新的随机样本，样本大小也是N。重复成千上万次，即可以得到成千上万组自助抽样的样本，得到成千上万个平均值和这些平均值的标准差。这样就得到了全世界人口身高的分布的标准偏差值估计了。

因此，自助抽样法的关键是以已知的观测样本为基础，找到一个重复模拟观测样本的方法。当①观测样本尺寸过小而不能直接作为全体样本统计的参考时，②统计量的理论分布未知或过于复杂时，或③存在指数计算但只存在少量起始样本时，自组采样法都可发挥作用。

[3]蒙特卡罗方法（Monte-Carlo method)，也称统计模拟方法，是20世纪40年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。通常蒙特卡罗方法通过构造符合一定规则的随机数来解决数学上的各种问题。对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题，蒙特卡罗方法是一种有效的求出数值解的方法。

[4]序列相关性，在计量经济学中指对于不同的样本值，随机干扰之间不再是完全相互独立的，而是存在某种相关性。又称自相关（auto correlation)，是指总体回归模型的随机误差项之间存在相关关系。

在回归模型的古典假定中是假设随机误差项是无自相关的，即在不同观测点之间是不相关的。如果该假定不能满足，就称与存在自相关，即不同观测点上的误差项彼此相关。

自相关的程度可用自相关系数去表示，根据自相关系数的符号可以判断自相关的状态，如果小于0，则V_t与V_t-1为负相关；如果大于0，则V_t与V_t-1为正关；如果等于0，则V_t与V_t-1不相关。