预测值标准差的测量与估计技巧

把同期数据分割成m份，然后对每份分别进行重复的MCP分析，得到m个预测值。预测值可以是平均风速和威布尔参数等。

令第j个预测值为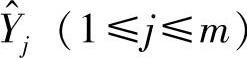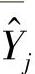，为m个预测值的均值，那么标准差的测量方法为

由于MCP分析对同期数据长度有要求，因此不可能把数据分割成很多份。实际工作中，往往测风塔实测数据长度仅有1年，因此很难进行切割。

Jackknife是统计学中常用的重新取样方法。Jackknife估计标准差的基本思想为：从整个样本空间中抽出一个或多个样本点后，系统地重复计算统计量估计。统计量的偏差和标准差可以通过新生成的统计量的变化情况计算。这样就可以不用切割风数据来估计MCP预测值的标准差了。

若在同期风数据中剥离一个数据子集，将导致MCP预测结果的变化。Jackknife标准差估计就是通过这种变化来估计MCP预测值的不确定性的。Jackknife法估计标准差的方法可用于任何MCP模型的不确定性估计，还可用于估计由MCP预测风数据推导的参数的不确定性，如威布尔参数或风力发电机的功率系数^[61]。

令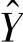为预测的平均风速或威布尔参数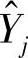；是第j（1≤j≤n)个同期数据序列的预测值。每个同期数据都缺失n分之一的数据（即剥离的数据子集)，这些数据子集各不相同也不重叠。那么对于整个风数据样本空间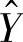，的标准差的渐进无偏估计可以表达为[61]

该方法假设剥离的n个数据子集之间相互独立。如果n个数据子集很短而相互关联，那么这个假设可能不成立，此时数据的序列相关性^[4]将对该方法产生影响。如果数据是独立的，那么随着数据样本空间的增大，Jackknife法估计的标准差将收敛于回归估计值。

把同期风数据分割成m份，并对每份进行n个数据子集的Jackknife计算。根据式（5-35)计算每份的Jackknife标准差，得到m个估计的标准差。(www.xing528.com)

令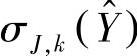为第k个Jackknife标准差，则m个Jackknife标准差的均值为

m个Jackknife标准差的标准差为

式（5-36)和式（5-37)可用于评估Jackknife标准差的均值及其置信空间。

Jackknife数据子集的最佳个数取决于同期数据的长度及其序列相关性。最佳的数据子集数目应该使测量的标准差与Jackknife标准差的差距最小，均方根误差最小。

测量的标准差与Jackknife标准差的均方根误差为

实验表明，RMSE对n的选择并不很敏感，说明序列相关性对Jackknife标准差的结果影响甚微^[61]。Anthony L。Rogers等人^[61]还指出，Jackknife法低估MCP预测的平均风速的标准差约38%，低估MCP预测的威布尔k参数标准差约18%，因此该方法存在改进空间。另外，同期数据点越少Jackknife标准差低估越严重。