简单线性模型优化：原理与应用

令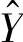为参考站平均风速在测风塔处的回归值或预测值，X为参考站同期平均风速。

一维线性回归模型1：

一维线性回归模型2：

一维线性回归是最常用的模型方法，尤其是模型1。线性回归模型首先要假设参考站点与测风塔的同期风速之间呈线性关系。对图5-4中的同期数据根据方法1进行回归分析，得到图5-5，回归模型的参数a=1。5132，b=0。2992，相关系数R²≈0。76。

因此，第i条数据的回归值为

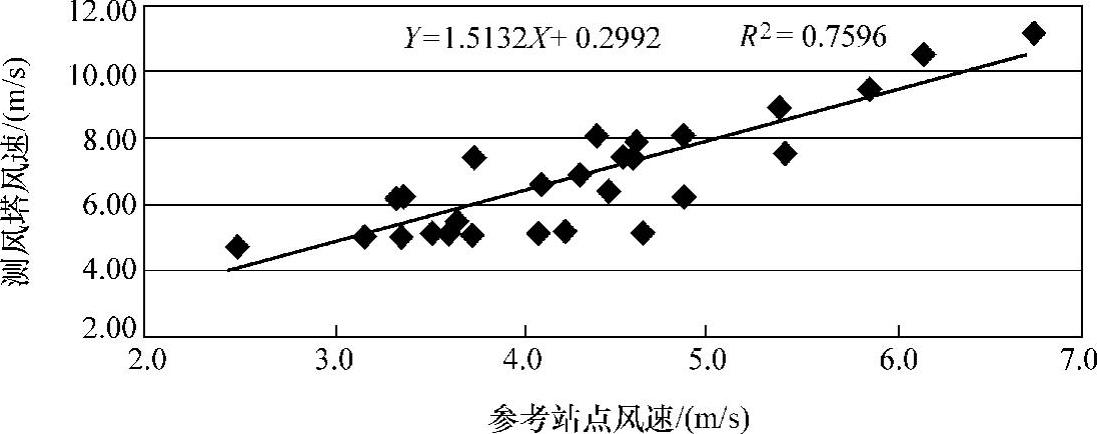
图5-5 线性回归分析（X轴为参考站点风速，Y轴为测风塔风速)

式（5-12)又称作传递函数，建立了参考站和测风塔风数据的关系。有了传递函数就可以轻松地把参考站点的风数据“传递”到测风塔处了。

图5-6展示了参考风数据的回归值时间序列曲线与测风塔实测数据的对比，可见回归值与测风塔实测值已经十分相似了。把式（5-12)应用于参考风数据的整个区间，即可以预测测风塔点的长期风速了，并得到长期的风数据时间序列，如图5-7所示。至此最简单的MCP过程，即“测量-相关-预测”过程便完成了。

Derrick^[54][55]把风数据分组成了12个扇区，然后对应扇区分别做简单线性回归分析。Derrick通过计算线性回归法的方差和协方差研究了预测风速的置信区间。通过对英国的数据进行分析，Derrick认为分散的数据点主要是由于具有显著等气压曲线的天气系统经过引起，且至少需要8个月的数据才能使结果的不确定度最小化。(www.xing528.com)

这种把风数据分组成多个扇区的方法不仅限于线性回归法。此时通常以参考风数据的风向分布为基准，且假设与测风塔处的长期风向分布是一致的。

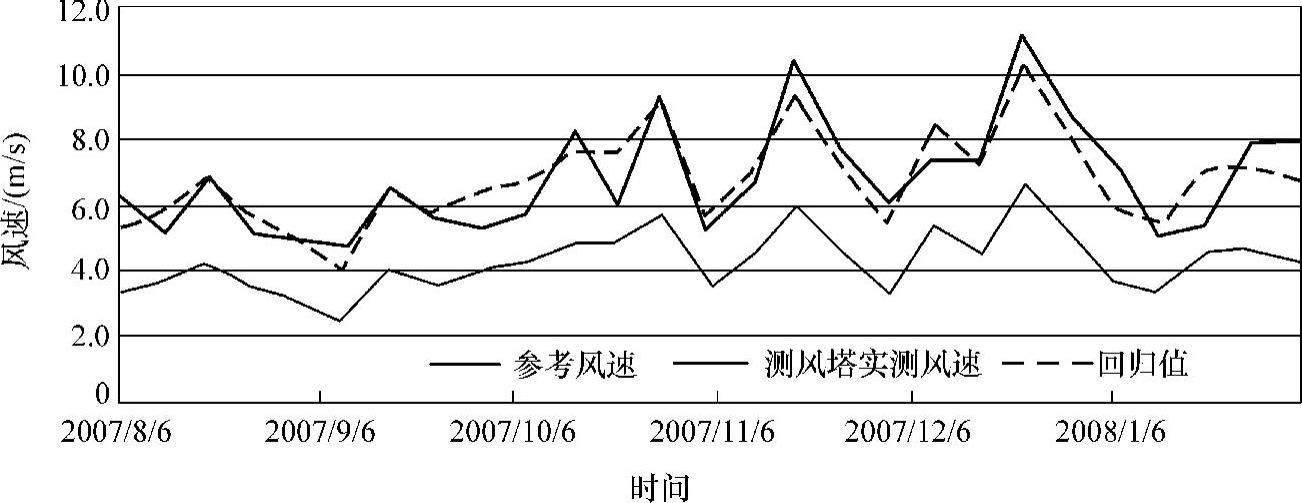
图5-6 线性回归值时间序列曲线与测风塔实测风速对比

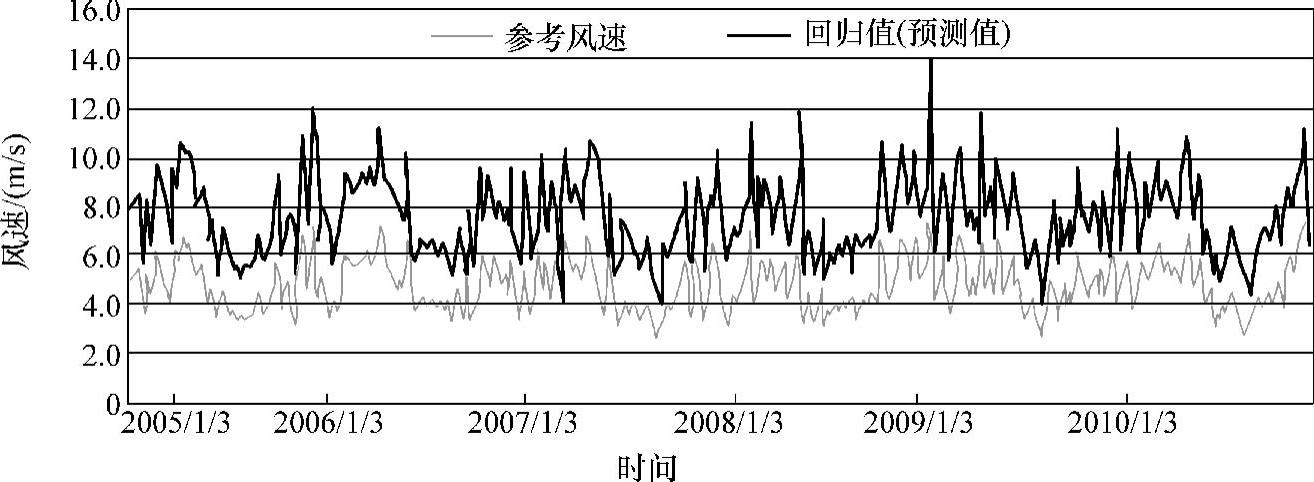
图5-7 MCP预测的平均风速时间序列曲线与原参考风数据对比

为了提高对风能的评估精度，Derrick还建议不使用低于4m/s的风速数据进行拟合^[55]。因为此时的风向仪很不稳定，且风力发电机在这样的低风速下并不发电。但是剔除低风速数据可能错误地估算整体的平均风速。

最简单的线性回归MCP方法没有考虑风向，因此显得粗糙。实际情况是，不同风向和不同的风速区间其相关性及回归模型可能各不相同。局地的风向可能被扭曲，导致测风塔实测数据的风向分布和参考数据有差异。因此好的MCP模型应该对这些复杂情况予以充分考虑。

风数据回归模型虽然复杂，但还是有标准对其优劣进行评价的。回归模型预测的风数据应该能够较好地表达测风塔实测风数据的：

1)平均风速；

2)威布尔分布参数；

3)测风塔处的年风能密度；

4)风向分布。