复杂地形修正方案

崎岖指数用来表征地形的复杂程度，是脱流程度或地形加速效应高估程度的间接量度。用预测站和参考站崎岖指数之差ΔRIX作为WAsP风流模型表现优劣的指标。

ΔRIX=RIX_WTG-RIX_MET （3-6）

式中 RIX_WTG——风力发电机点位，即预测站的崎岖指数；

RIX_MET——测风塔点位，即参考站的崎岖指数。

如果预测站和参考站的地形复杂（崎岖）程度相同（ΔRIX≈0），预测误差相对较小。如果参考站比预测站地形更加复杂（ΔRIX＜0），则预测结果被明显低估。相反的，如果参考站比预测站地形更简单（ΔRIX＞0），则预测结果被明显高估了^{[18][37][40][41]}。

Bowen等人^[18][41]对葡萄牙一个风场的案例进行研究，得出了WAsP对平均风速的预测误差与ΔRIX的关系，如图3-3所示。该风场地形复杂，共有5个测风塔，采用交叉预测的方法，得出25个预测的平均风速，并用下式表达与实测风速的误差：

式中 U_p——预测的平均风速；(www.xing528.com)

U_m——实测的平均风速。

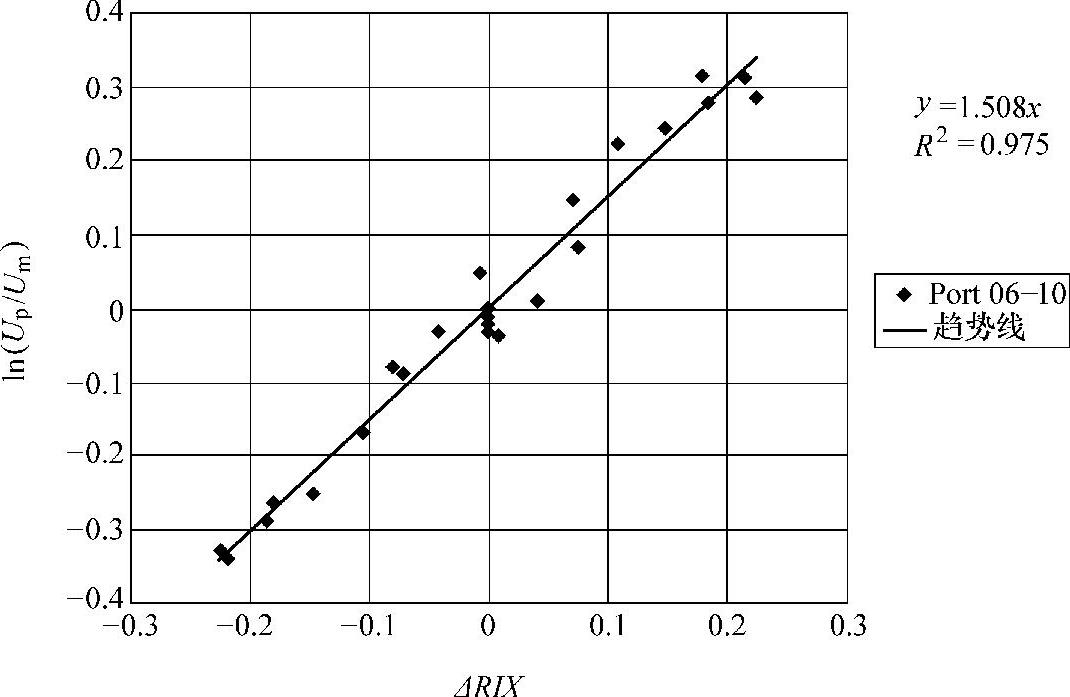
图3-3 WAsP对平均风速的预测误差与ΔRIX的关系曲线[18]

由图3-3可见，趋势线为线性的，并通过原点（0，0），即预测的平均风速与实测平均风速的比值的对数与ΔRIX呈线性关系。图3-3中还标示了直线的斜率和拟合度系数（0.975）。于是，可以推导出如下经验关系式：

式中 α——回归曲线的斜率。

可以根据ΔRIX值，由上式对预测的平均风速进行修正。对于该风场实例，经ΔRIX修正后，WAsP模型的发电量预测结果改善了69%（100%为预测无误差）。ΔRIX值大于5%的情况下，两个测风塔交叉预测的结果改善平均超过90%^[18]。由此可知，对于地形复杂的风场，至少需要安装两个测风塔才能对风场的发电量进行较为满意的预测。