图2-10为在Askervein山顶上和上风向同步测量的风垂直轮廓线。平地上的垂直风加速廓线为对数形式，但是在山顶上距离地面高度为l处存在一个拐点，为最大相对风加速度的高度。在拐点之上，风加速廓线呈直线，直到与上风向风加速廓线相交于高度为2L处。L为山体的特征高度，通常为山体半宽的高度，l和L的定义如图2-11所示。
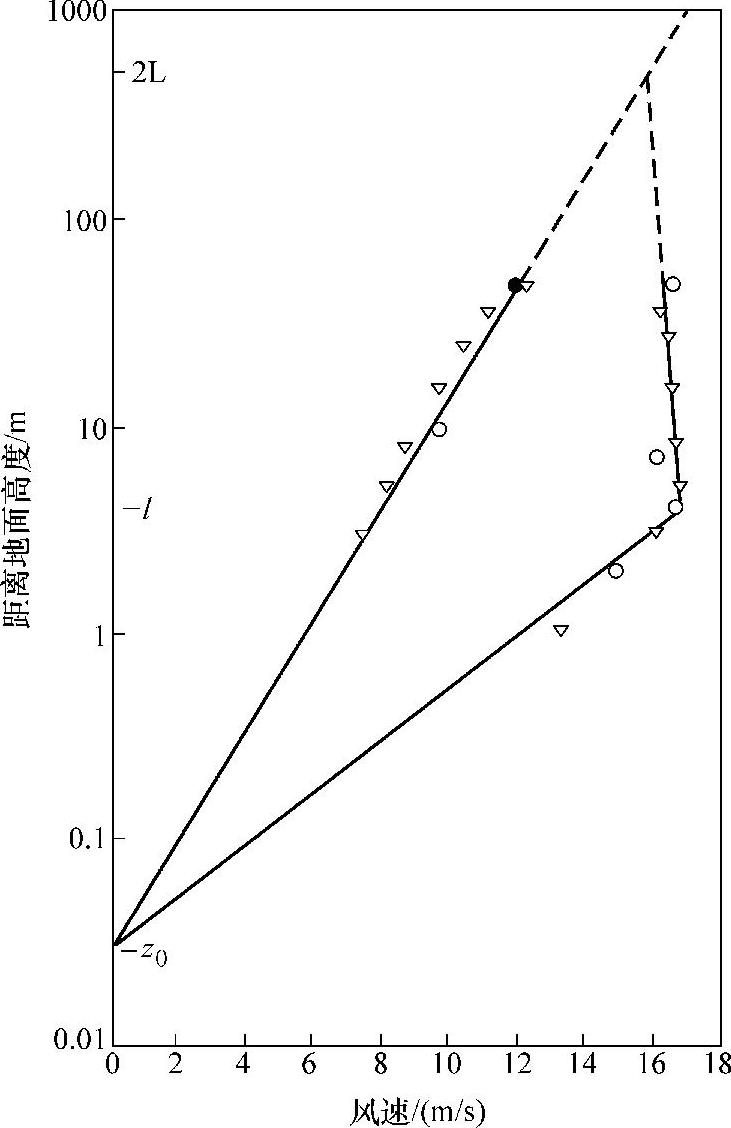
图2-10 在Askervein山顶上和上风向同步测量的风垂直轮廓线[11]（纵坐标为距离地面实际高度的对数。图中符号代表测量的平均风速；左侧直线代表上风向未受山体影响的风加速廓线；右侧直线代表山顶上的风加速廓线）
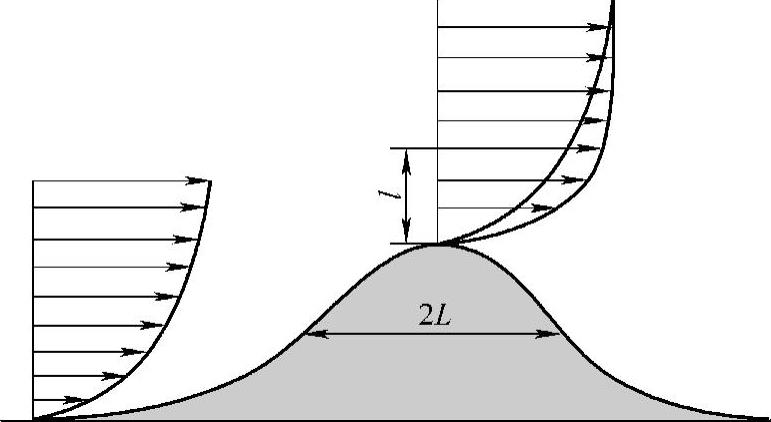
图2-11 风流过理想化的山体时，上风向和山顶上的垂直风廓线[4]
风加速度ΔS和l的近似表达式为[11]
(www.xing528.com)
当山体垂直于风向的维度比L大得多时（坡度较小），该式可以得到较好的结果，因此风加速问题可以认为是二维的。
上述的例子很清晰地表明，地形对风流的影响是十分明显的。但是应该注意，所有地形高度的变化都会影响风流：地形高度增加5%，可能对平均风速产生5%的影响（可能在轮毂高度处），进而导致近15%的风能密度的增加[4]。对于复杂地形，通常很难甚至不可能用式（2-10）和式（2-11）来计算特定地点的风资源，因此很多情况下都需要使用数值模型进行计算。
有些情况下，“距地面高度”的准确表达并不清晰。作为例子，想象位于一个低矮山顶上的风力发电机组：如果山体的高度和风力发电机组的轮毂高度比很小，且山坡陡峭，那么该山体可以认为是风力发电机组的基础，增加了风力发电机组的轮毂高度。但如果山体的横向和纵向维度增加，情况就发生了变化，相对轮毂高度就变成了距离山顶地面的高度。
另一个例子是风力发电机组位于断崖附近的情况，这种情况海边较为常见，如图2-12所示。当风来自海面时，我们可能会试图使用从水面到轮毂高度的距离作为相对高度。但这样做是非常错误的，因为在风远未到达陆地时，就已经受到了悬崖的影响，因此相对高度为距离地面的高度。
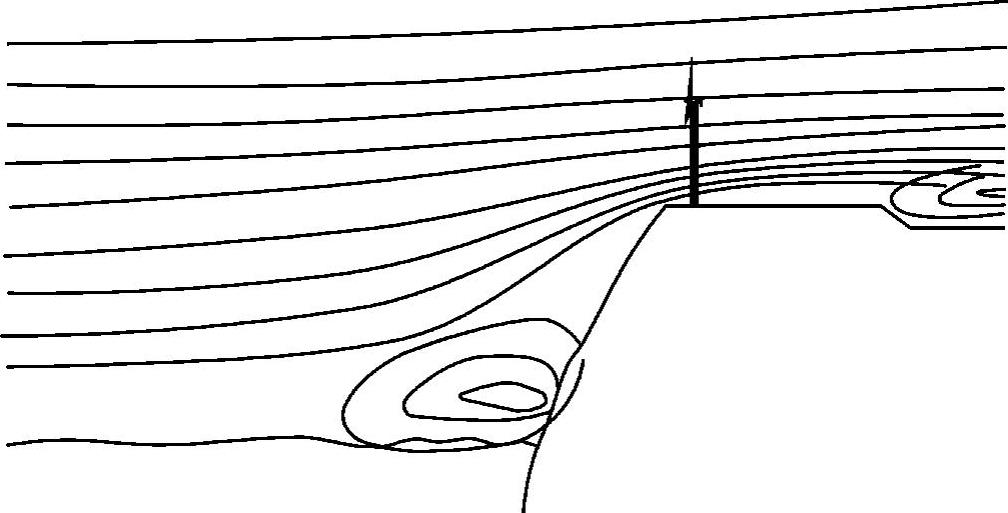
图2-12 悬崖地形对风的影响
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
