地表粗糙度长度及其影响分析

地表粗糙度由地表粗糙元的尺寸和分布决定。对于陆地表面，粗糙元主要有植被、建筑区和土壤表面。关于粗糙度的概念在本书的第10章中还有进一步的讲解。地表粗糙度是作为大气下边界出现的几何长度，是对数风廓线中平均风速等于零的高度。中性稳定大气近地层的风廓线为

式中 z₀——地表粗糙长度，单位为m；

u_∗——具有速度量纲的非负常数，称为摩擦速度。

u_∗的二次方具有湍流切应力的性质。根据粗糙度的概念，当平均风速u（z）为零时的高度就是z₀。根据式（2-1）可知，只要测量两个高度的平均风速，就可以很容易地推导出u_∗和z₀，也可以根据对数函数的外推，估算平均风速为零时的高度。

虽然粗糙长度不等于每个地表粗糙元的高度，但是这些粗糙元与粗糙长度却存在着一一对应的关系。换句话说，一旦确定了某一特定表面的粗糙长度，它将不随风速、大气稳定度和应力而改变。当地表粗糙元改变时，例如植被高度和覆盖率的变化、竖起篱笆、建造房屋和森林砍伐等，粗糙长度才可能变化。粗糙元的高度越高，粗糙长度越大，但是粗糙长度总是小于粗糙元的物理高度。

Lettau于1969年提出了粗糙元与粗糙长度的简单经验关系式^[5]。可以用高度h、迎风面的截面积S描述粗糙元的形态。如果多个粗糙元均匀地分布在一个区域范围内，那么平均每个粗糙元所占的面积为A（总面积/粗糙元个数），则有

当粗糙元分布均匀、彼此之间缝隙较大、大小和形状类似时，根据式（2-2）计算的结果是可以接受的。计算粗糙元迎风面的截面积S时，应该考虑孔隙率，如树林和树丛等。

【例2-1】 一块均匀分散着小树丛的陆地，面积为5000m²。单个树丛的平均高度约为50cm，平均宽度约为1m，这块地上大约有500个这样的小树丛。由于盛夏季节，树叶饱满，孔隙率取20%，求这块地的粗糙长度？

每个树丛作为一个粗糙元，其迎风面的截面积为

S=1×0.5×（1-20%）m²=0.4m²

平均每个粗糙元所占的面积为

A=5000/500m²=10m²

于是，粗糙长度为

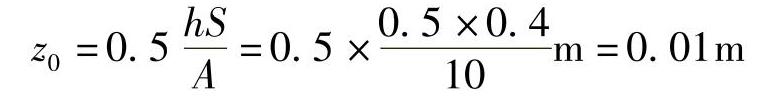
实际工作中，经常会遇到多种大小和形状不同的粗糙元混合的情形。为了计算这种情形下的粗糙长度，Kondo和Yamazawa于1986年提出了类似的经验关系式^[6]：

(www.xing528.com)

式中 S_i——第i个粗糙元的迎风面截面积；

h_i——第i个粗糙元的高度；

S_T——n个粗糙元所占的总面积。

水的表面情况比较特殊，因为水波是动态的，水波的振幅与风速有关。当不考虑粘性效应和水的表面张力时，Charnock于1955年提出了估算水面粗糙度的经验公式^[7]：

式中 b——常数，约等于0.014；

g——重力加速度；

u_∗——摩擦速度。

对海洋表面的粗糙长度讨论，应该区分光滑流和粗糙流。实验表明，在风速小的开阔洋面上，层流厚度可覆盖水面涟漪所构成的粗糙元，故认为是光滑流，此时粗糙长度随着风速的增大而减小。而当风速进一步增大后，洋面等大水体表面上粗糙长度的取值将与波浪的起伏状况有关，这时的流动称为粗糙流。式（2-4）就是针对这种粗糙流，并假设海洋波浪属于重力波，波浪的高低与近地层风切变强度有关，表明开阔水面上粗糙长度随风速增大而很快增大。虽然水面的粗糙长度并不固定，但是因为非常小，一般的风资源软件模型中把它简化成固定值（如0.0002m），但是在模拟开阔水面上的湍流时，通常不能这样简化。

在风资源和微观选址工程应用中，一般不会直接计算粗糙长度。上面的计算过程意在使读者更好地了解粗糙长度的影响因素和物理特征。实际工作中，通常通过经验，根据地表粗糙元的特征进行估计。

根据长时间的各地观测结果，归纳得出的各种地表粗糙长度z₀的典型值如图2-1所示^[89，4]。

图2-1 各种典型地表形态的粗糙长度^[4]

地表粗糙长度受季节影响非常大，如北方冬天冰雪覆盖，粗糙长度为0.001m，而夏天的农田则被庄稼覆盖，粗糙长度为0.05m，是冬天的50倍！因此，在风资源与微观选址工作中，通常只能选用年均粗糙长度。准确评估年均粗糙长度无疑是困难的，理论上可以根据不同季节的平均风速进行加权平均，但实际操作仍然极其困难。

最简单的方法，也是必要的步骤，是在初步设置好粗糙长度后，用同一测风塔不同测风高度的平均风速相互推算，看推算值与实测值是否一致（或非常接近），如果不一致，则需要重新调整粗糙长度的设置，直到得到满意的结果为止。

这里提到的年平均概念贯穿风资源评估工作的始终，如年平均大气稳定度、年平均空气密度、年平均风速等。因为气象问题十分复杂，时刻都在变，随机性很大，以目前的计算水平，不可能进行长期连续的模拟计算，所以这种简化是绝对必要的。

应该注意的是，应该把粗糙长度当作气象参数对待，而计算风力发电机组的发电量也应该是基于气象学，这主要是因为季节更替和天气的变化无常。