《逻辑代数基础》之拓展的介绍

1.逻辑函数

（1）逻辑函数定义。

逻辑函数是指以逻辑运算为基础，以逻辑变量为运算对象，输入变量和输出变量的值只能取逻辑值的函数。可表示为

（2）逻辑函数的表示方法。

逻辑函数常用的表示方法有逻辑表达式、真值表、逻辑图、波形图和卡诺图。

①逻辑表达式。由逻辑变量和逻辑运算符构成的式子，称逻辑表达式。在逻辑表达式中，逻辑运算的优先顺序是非运算、与运算、或运算。_若要改变运算顺序时需加括号，如

②真值表。将输入变量的各种取值与输出变量的对应关系用表格的形式表示出来，称为真值表，如的真值表如表2-16所示。

表2-16　F=的真值表

由表2-16可见，逻辑函数的真值表是由逻辑运算得到的。列真值表时，需将输入变量的取值组合按二进制数从小到大的顺序依次列出，然后将其代入逻辑函数表达式中进行逻辑运算，得到每一取值组合所对应的输出值，填入到真值表的输出列。

反之，如果已知逻辑函数的真值表也可以写出其逻辑表达式。方法如下。

第一步：写出真值表中输出变量值为1的组合对应的与项，在与项中输入变量取1的为原变量，输入变量取0的为反变量，如表2-16中的输入变量A、B分别取0、1和1、0时输出值为1，其对应的与项分别是

第二步：将各与项进行或运算，即为逻辑函数的输出表达式。由表2-16所写出的逻辑函数表达式为

③逻辑图。用逻辑符号表示逻辑函数中的逻辑关系，称为逻辑图。函数的逻辑图如图2-52所示。

④波形图。

它指用于反映输出变量和输入变量在时间上的对应关系的图形。函数的波形图如图2-53所示。

图2-52　函数F=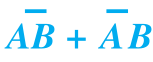的逻辑图

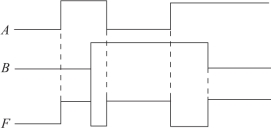
图2-53　函数F=的波形

⑤卡诺图。

卡诺图是逻辑函数最小项的图形表示。

a.最小项。对于n个变量的逻辑函数，若某个与运算项中，包含了全部的n个变量，且每个变量都是以原变量或反变量的形式仅出现一次，则称这个与项为该逻辑函数的最小项。

n个变量有2n个组合，若用原变量表示1，反变量表示0，则每一个组合所对应的与项都是最小项，故n个变量有2n个最小项。例如，3个变量有23=8个最小项，分别是

最小项除用与表达式表示外，还常用mi表示，其中i为最小项取值所对应的十进制数。即3个变量的最小项可表示成m0、m1、m2、m3、m4、m5、m6、m7。

b.卡诺图。将n个变量的2n个最小项分别用2n个逻辑相邻的小方格表示，即为卡诺图。逻辑相邻是指两个最小项中只有一个变量取值不同，其余全相同。

2个、3个、4个变量的卡诺图的结构如图2-54所示。由图可见3个、4个变量的逻辑函数的卡诺图在结构安排上作了调整，目的是要保证位置相邻的小方格中的最小项逻辑相邻。

图2-54　卡诺图结构

（a）二变量卡诺图；（b）三变量卡诺图；（c）四变量卡诺图

c.逻辑函数的卡诺图。根据逻辑函数的与或表达式，在卡诺图中将表达式包含的最小项所对应的小方格内填“1”，其余或填“0”或不填。

如逻辑函数的卡诺图如图2-55所示。

逻辑函数的各种表示方法可以相互转换。如由逻辑图可写出逻辑表达式，反之由逻辑表达式也可绘出逻辑图；由逻辑表达式可列出真值表，反之由真值表也可写出逻辑表达式；由逻辑表达式可作出卡诺图，反之由逻辑函数卡诺图也可写出逻辑表达式等。

2.逻辑函数化简

逻辑函数化简是逻辑电路分析和设计的关键步骤。在分析逻辑函数时，如果逻辑函数的表达式简单，逻辑运算工作量就小。而在逻辑电路设计中，如果逻辑函数表达式简单，所需的逻辑器件就少，电路就相对简单。逻辑函数的化简方法有公式法和卡诺图法。

（1）公式法。

逻辑函数的公式化简法，就是利用逻辑运算的基本定律和常用公式，进行合并、吸收等操作，使逻辑表达式的与项最少，与项中的变量最少。由化简所得到的逻辑表达式称为最简与或式。

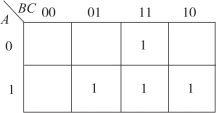
图2-55　逻辑函数的卡诺图(www.xing528.com)

①逻辑运算基本定律。

0-1律：A·0=0　A+1=1

自等律：A ·1=A　A+0=A

互补律：

交换律：A+B=B+A　A·B=B·A

结合律：（A+B）+C=A+（B+C）　（A·B）·C=A·（B·C）

分配律：A·（B+C）=AB+AC　A+（B·C）=（A+B）（A+C）

重叠律：A·A=A　A+A=A

反演律（_摩根定理）

非非律：

②逻辑运算常用公式。

③逻辑运算基本规则。

代入规则：用一个函数替代逻辑等式中的某一变量，等式仍然成立。

反演规则：将逻辑函数F中的“与”变成“或”，“或”变成“与”，0变成1，1变成0，原变量变成反变量，反变量变成原变量，即得F的反函数，用表示。

对偶规则：将逻辑函数F中的“与”变成“或”，“或”变成“与”，0变成1，1变成0，即得F的对偶式，用F′表示。若两个函数F1和F2相等，则它们的对偶式F′1和F′2也相等。

④化简举例。

（2）卡诺图法。

①化简步骤。

第一步：作出给定函数的卡诺图。

第二步：画“卡诺圈”。即将卡诺图中相邻为“1”的2n个小方格圈起来。画“卡诺圈”的原则是“能大不小”，即卡诺圈中的小方格数取最大数。因为“卡诺圈”越大，化简后与项中变量的个数越少。

第三步：合并最小项。即对每一个“卡诺圈”中的各最小项，“留同舍异”得到一个新的与项，每个卡诺圈合并后的与项进行或运算。

②化简举例。

【例2.4】化简函数

解：函数的卡诺图如图2-56所示。

由卡诺图得：F=AB+BC+AC

【例2.5】化简函数F（A，B，C，D）=∑m（0，1，2，4，6，7，8，10，11，12，14）。

解：函数的卡诺图如图2-57所示。

图2-56　【例2.4】的卡诺图

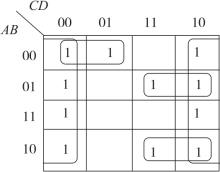
图2-57　【例2.5】的卡诺图

由卡诺图得：

【注释】

[1]居里温度是指磁性材料中自发磁化强度降到零时的温度，是铁磁性或亚铁磁性物质转变成顺磁性物质的临界点。低于居里温度时该物质称为铁磁体，此时和材料有关的磁场很难改变。当温度高于居里温度时，该物质称为顺磁体，磁体的磁场很容易随周围磁场的改变而改变。

[2]74和54是国际通用的系列标志，74为民用，温度范围为0～+70℃，电源电压范围为5V±5%；54为军用，温度范围为-55℃～+125℃，电源电压范围为5V±10%。

[3]LS：74LS和74ALS；ALS：先进低功耗肖特基。肖特基二极管是一种低功耗、超高速半导体器件，具有正向压降小、反向恢复时间极短等特点。

[4]CMOS（Complementary Metal Oxide Semiconductor，互补金属氧化物半导体），是制造大规模集成电路的一种技术或芯片。

[5]HC：高速CMOS；HCT：高速CMOS，与TTL兼容，可互换使用。

[6]数字逻辑电路分为组合逻辑电路和时序逻辑电路两类，时序逻辑电路是指电路在任一时刻的输出不仅与该时刻的输入信号有关，还与电路原来的状态有关；而组合逻辑电路的任一时刻的输出仅和该时刻的输入有关。