1.基尔霍夫定律及应用
基尔霍夫定律(Kirchhoff laws)是分析复杂直流电路的最基本定律,反映的是电路中各电流和各电压的相互关系。基尔霍夫定律包括电流和电压两个定律,分别称为基尔霍夫第一定律和基尔霍夫第二定律。
1)基尔霍夫第一(电流)定律(KCL)
(1)内容。
在电路的任一节点上,流入或流出节点的电流的代数和等于零。一般形式为
![]()
节点是指电路中3条或3条以上支路的汇集点;支路是指至少含有一个电路元件且流过同一电流的分支电路。
(2)应用。
用基尔霍夫第一定律分析、求解电路时,需先设电流的参考方向,再按假定的正、负方向,列电流方程。通常设流入节点的电流为正,流出节点的电流为负。图1-48所示的电路中,因b、c为同一节点,故在图示电流参考方向下,节点a、b(c)、d的电流方程分别为
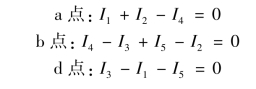
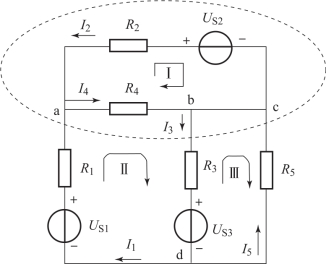
图1-48 基尔霍夫定律示意图
(3)推广。
基尔霍夫第一定律虽然是描述节点电流关系的,但同样适用于包围几个节点的闭合面。如对图1-48所示电路中的虚线包围的闭合面,有
![]()
2)基尔霍夫第二(电压)定律(KVL)
(1)内容。
在任一个闭合回路中,按一定方向绕行一周,各段电压的代数和等于零。用电压方程表示为
![]()
(2)应用。
根据基尔霍夫定律列回路电压方程,首先应假定各段电压的参考方向和回路的绕行方向,然后按照“在绕行方向上,电位降低电压为正,电位升高电压为负”的方法列回路电压方程。电压又称为“电压降”,电压的正方向就是电位降落的方向。对于电阻,电流的方向是电位降落的方向;对于电源,从正极到负极是电位降落的方向。如图1-48所示电路,在图示的回路绕行方向下,回路Ⅰ、Ⅱ、Ⅲ的电压方程分别为
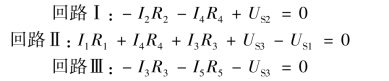
(3)推广。
基尔霍夫电压定律虽然是描述闭合电路电压关系的,但如果将开路电压计入回路电压方程中,也适用于非闭合回路情况。在图1-49所示电路中,图示回路绕行方向下,可列出电压方程为
![]()
也可直接写成
![]()
3)用基尔霍夫定律分析电路的方法
用基尔霍夫定律分析和求解具有多个回路的复杂电路时,要通过列、解方程的方法进行,一般步骤如下。(https://www.xing528.com)
(1)在电路中设出各支路的电流参考方向和回路的绕行方向。
(2)根据基尔霍夫第一定律和第二定律,列出独立的节点电流方程和回路电压方程。
独立的节点电流方程是指任意一个方程都不能由其他方程线性组合得到。对于有n个结点的电路,最多只能列出n-1个独立的节点电流方程。
如果电路中有m条支路,则求解m条支路的电流需m个方程,在列出n-1个独立的节点电流方程后,还需要列m-n+1个回路电压方程。
(3)联立,求解方程组,得各支路电流。
当只需了解某一支路电流和某一元件的电压时,可以采用戴维南定理,将被求支路以外的部分,视为一个有源二端网络并将其等效成一个电压源。
2.戴维南定理及应用
(1)戴维南定理(Thevenin's theorem)的内容。
任意一个有源二端网络都可以用一个等效电压源代替,该等效电压源的电动势等于有源二端网络的开路电压,内电阻等于二端网络所有电源不起作用时端口的等效电阻。
电压源是电源的模型之一,是由恒压源和内电阻串联而成,如图1-50(a)所示。恒压源是电源的理想化模型,是忽略电源内电阻的电压源。电源的另一种模型为电流源,是由恒流源和内电阻并联而成,如图1-50(b)所示。
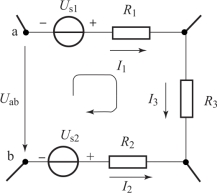
图1-49 非闭合电路
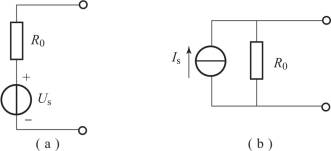
图1-50 电源模型
(a)电压源;(b)电流源
(2)戴维南定理的应用。
用戴维南定理分析、计算电路的一般步骤如下。
①断开待求支路,将待求支路以外的电路作为有源二端网络,如图1-51所示。
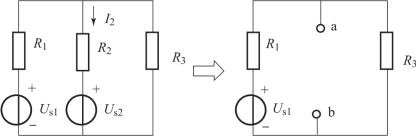
图1-51 有源二端网络
②求二端网络的端口处的开路电压,如图1-51所示的开路电压Uab。
由图可知
![]()
③令二端网络中,所有的电源都不起作用,求端口等效电阻。对不起作用电源的处理方法是:电压源视为短路,电流源视为开路,如图1-52所示的端口等效电阻Rab。

图1-52 有源二端网络电阻等效电路
由图可知
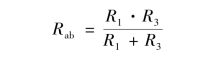
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




