分析比例导引的过载特性

不考虑制导动力学的比例导引制导框图如图1.4 所示， 其中ε 表示初始速度指向误差， 在图1.4 中的误差引入点， 误差输入为VMε。

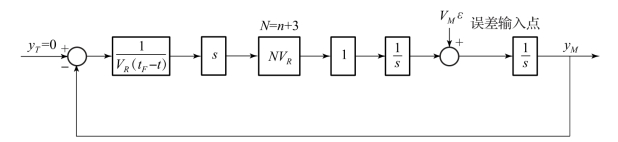
图1.4　不考虑导动力学的比例导引制导框图

由图1.4 可知， 从VMε 到yM 的传递函数可以表示为

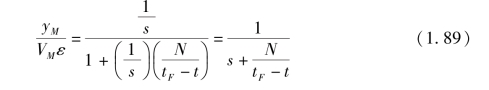
或者， 表示成如下的微分方程形式：

求解式（1.90） 微分方程得到

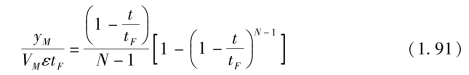(www.xing528.com)

或者， 将N ＝n+3 代入式（1.91）， 又可得到

从式（1.91） 和式（1.92） 可以看出， 针对图1.4 所示的无动力学滞后的简单系统， 导弹在t ＝tF 的末端时刻总是能击中目标， yM ＝yT ＝0。

分别对式（1.91） 进行一次求导和二次求导， 得到

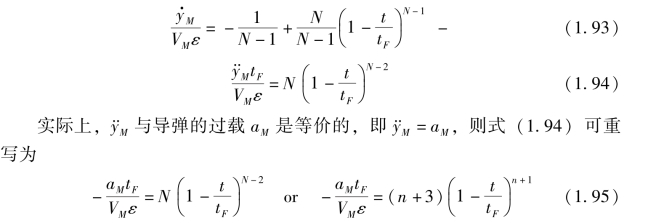
通过式（1.95） 或图1.4， 容易得到由初始速度指向误差驱动的比例导引无量纲过载随N 的变化曲线， 如图1.5 所示。 由此可见， 当N ＝3 时， 比例导引的过载随时间变化按线性关系收敛到0； 当N≥2 时， 比例导引的终端过载均收敛到0， 但较大的N 选值会导致导弹在初始阶段面临过载饱和的危险，因此N 也不宜过大； 当N ＝2 时， 比例导引的过载为恒定值2， 不随时间变化； 当N ＜2 时， 如N ＝1， 则比例导引的终端过载是发散的， 通常情况下这是不希望出现的， 但如果导弹过载能力允许， 也可以刻意利用这种规律来实现某些方案弹道设计， 以达到特定的目的［33］。

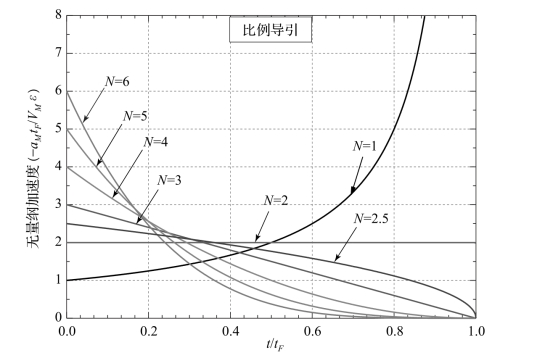
图1.5　由初始速度指向误差驱动的比例导引无量纲过载随N 的变化曲线