二次型最优控制理论与比例导引证明

系统状态方程表示为

式中， x 为m1 维状态向量； u 为满足解存在唯一性条件的m2 维控制向量； A、B 分别为满足解存在唯一性条件的m1 ×m1 维状态矩阵、 m1 ×m2 维控制矩阵。

系统状态初值表示为

目标函数表示为

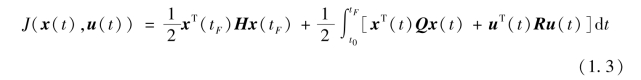
式中， t0 为起始时刻； tF 为终端时刻； H 为m1 ×m1 维半正定的终端加权矩阵； Q 为m1 ×m1 维半正定的状态加权矩阵； R 为m2 ×m2 维正定的控制加权矩阵。

系统最优控制表示为［29］

其中， P 是如下Riccati 方程的解：

且P（tF） 满足如下关系：

式（1.4） ～式（1.6） 即为方程（1.1）、 方程（1.2） 表示的系统在以式（1.3） 为目标函数时的二次型最优控制结果。 下面利用上述结论来讨论经典比例导引的证明过程。

以纵向平面运动为例， 建立图1.1 所示弹目运动几何关系。 图1.1 中，LOS 表示当前弹目视线（line of sight）， （xM， yM） 表示导弹的位置， （xT， yT）表示目标的位置， VM 表示导弹速度， ac 表示导弹加速度指令， θ 表示弹道倾角； VR 表示弹目相对速度。(www.xing528.com)

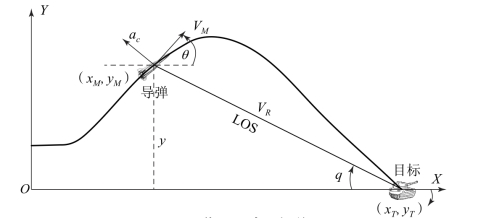
图1.1　弹目运动几何关系

根据上述几何关系， 定义

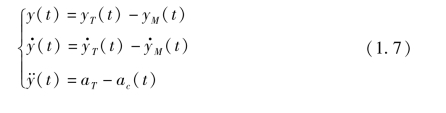
为简化起见， 式（1.7） 写成

将式（1.8） 表示成框图的形式， 如图1.2 所示。

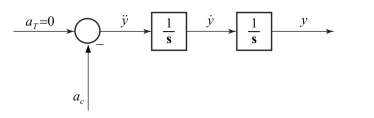
图1.2　弹目运动几何关系的框图表示

暂不考虑目标机动， 根据式（1.8）， 系统的状态空间方程为

进一步整理， 得到如下3 个微分方程：

将矩阵P（t）、 控制加权矩阵R、 控制矩阵B 代入式（1.4） 中， 得到式（1.7） ～式（1.9） 所示系统的最优解

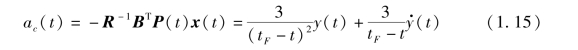
式（1.15） 即为纵向平面内经典比例导引的相对位置、 相对速度、 剩余飞行时间的表示形式， 其导航系数为常值3。