圆曲线测量技术详解

圆曲线的主点ZY、QZ、YZ定出后，为在地面上标定出圆曲线的形状，还必须进行曲线的详细测设工作。曲线点的间距，一般规定：R≥150 m时曲线点的间距为20 m，50 m≤R＜150 m时曲线点的间距为10 m，R＜50 m时曲线上每隔5 m测设一个细部点，在地面点上要钉设木桩，在地形变化处还要钉加桩。

圆曲线的详细测设方法有偏角法、切线支距法、弦线支距法、弦线偏角法、极坐标法和GPS-RTK法等，下面主要讲解偏角法、切线支距法、极坐标法和GPS-RTK法。

4.2.3.1　偏角法（长弦偏角法）

偏角法实质就是极坐标法，如图4-3，它是以曲线起点或终点至曲线上任一点P的弦线与切线T之间的弦切角（偏角）和弦长C来确定P点位置的方法。

偏角法测设圆曲线

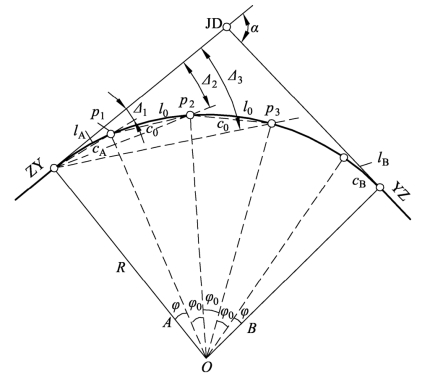
图4-3　偏角法测设圆曲线

（1）偏角的计算。

偏角法测设曲线，通常采用整桩号设桩，由几何原理可知，偏角δ等于相应弧（弦）所对圆心角的一半，即

曲线上其他各整桩号上的偏角为：

式中：l为弧长，一般为20 m，当半径R较小时，l取10 m。由此可知，只要曲线半径R和曲线桩号至曲线起点（或终点）的弧长已知，就可以算出弦切角δ和弦长C，从而可以定出曲线上的桩号。

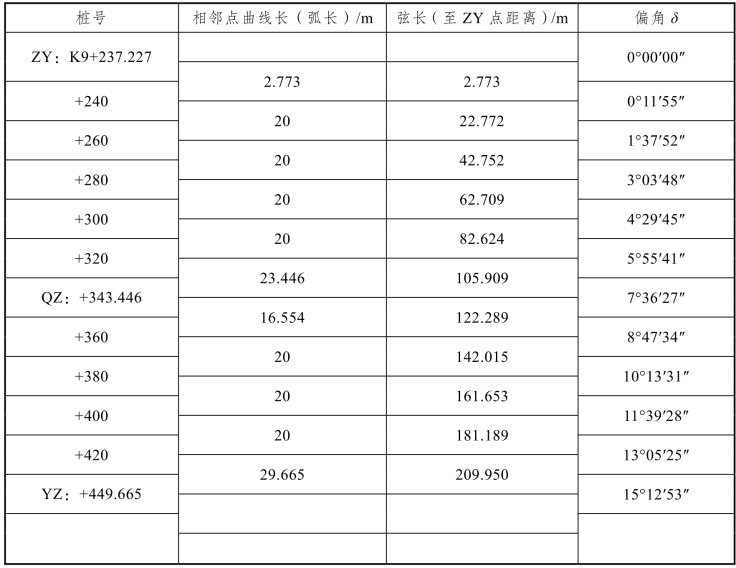
【例4-3】已知Yα=30°25′46″，R=400 m，JD5里程桩号为K9+346.015，计算曲线要素和主点里程，曲线上加桩间隔为20 m，试计算详细测设数据。

【解】根据已知条件，计算曲线要素得：T=108.788 m，L=212.438 m，E=14.530 m，其他计算数据见表4-1。

表4-1　偏角法测设圆曲线计算

（2）偏角的测设方法。

对于同一条曲线在不同的主点安置经纬仪测设辅点时，因照准部转动方向不同，有正拨和反拨之分。当顺时针方向转动，即依次测设曲线各加密点（辅点）度盘数逐个增加时，称为正拨；反之称为反拨。

由上例可知，路线右转时，在ZY点安置仪器，角度为正拨，其测设步骤为：

① 在ZY点安置仪器，瞄准交点J5D，水平度盘配盘为0°00′00″，此方向即切线方向；

② 转动照准部，使水平度盘读数为0°11′55″，在此方向自ZY点量距2.773 m，得桩号为K9+240；

③ 继续转动照准部，使水平度盘读数为1°37′52″，自ZY点量距22.772 m（弦长），得桩号K9+260；

④ 依次类推测出曲线其余各桩号。

当测至曲中点QZ点和YZ点时，应与曲线主点测得的QZ点重合，若不重合，闭合差一般不超如下规定：

否则，应查明原因，进行纠正或重测。实际测设中，为了提高测设精度，一般从曲线起点ZY点和终点YZ点上分别测设曲线的一半，在曲线中点QZ处检核。

4.2.3.2　切线支距法

切线支距法又称直角坐标法，它是以曲线起点（ZY）或终点（YZ）为原点，以切线方向作为坐标纵轴x，过原点的半径方向作为横轴y，建立直角坐标系。利用曲线上各点的坐标x、y值放样出曲线上的各点。在实际施工测量中，一般采用整桩进行设桩，如图4-4，li为待测点至原点ZY的弧长，iφ为li所对的圆心角，R为曲线半径，则pi点的坐标为：

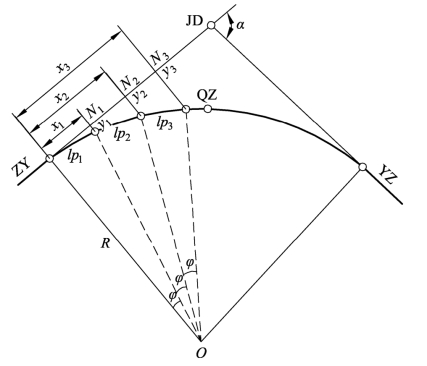
图4-4　切线支距法测设圆曲线

在实际施工测量过程中，为了避免支距过长，一般采用由ZY、YZ点向QZ点进行施测，具体施测步骤为：

（1）在ZY（或YZ）点安置仪器，瞄准切线（即JD）方向，用钢尺量距xi，得垂足Ni。

（2）在Ni点架设仪器，后视ZY（或YZ）点，拨90°，转向圆心方向，再用钢尺量距yi，即可定出曲线点pi。

（3）曲线上各点施测完成后，要量取曲线中点至最近的一个曲线桩点间的距离，比较桩号之差与实测距离，若二者之差在限差之内，则测设合格；否则查明原因，予以纠正。

切线支距法适用于平坦开阔地区，有桩号误差不累积的优点，但效率低，对自然环境要求高，在全站仪没有普及时，有时采用该方法进行检核，目前外业工作中基本不用该种测量方法，只是利用该公式进行编程计算。

4.2.3.3　极坐标法(www.xing528.com)

用极坐标法测设圆曲线细部点时，要先计算各细部点在测量平面直角坐标系中的坐标值，测设时，全站仪安置在平面控制点或已知坐标的线路交点上，输入测站坐标和后视点坐标（或后视方位角），再输入要测设的细部点坐标，仪器即自动计算出测设角度和距离，据此进行细部点现场定位。下面介绍细部点坐标的计算方法。

（1）计算圆曲线主点坐标。

如图4-5（a），可以由JD1（x1，y1）和JD2（x2，y2）的坐标，利用坐标反算公式计算第一条切线的方位角αJ1—J2：

第二条切线的方位角αJ2—J3可由JD2、JD3的坐标反算得到，也可由第一条切线的方位角和线路转角推算得到，即αJ2—J3有：

根据方位角αJ1—J2、αJ2—J3和切线长度T，用坐标正算公式计算曲线起点（ZY点）坐标（xZY ，yZY）和终点（YZ点）坐标（xYZ，yYZ），则起点（ZY点）和终点（YZ点）坐标分别为：

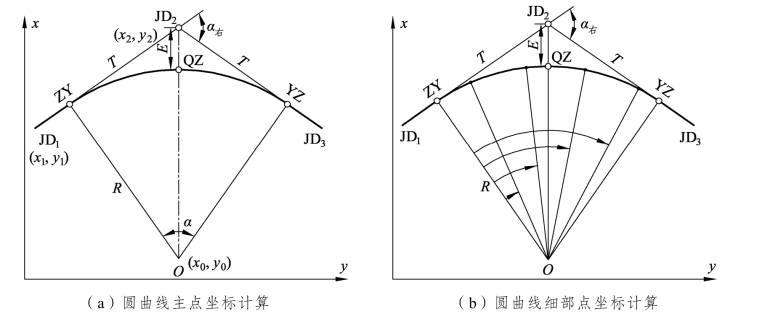
图4-5　圆曲线坐标计算

曲线中点坐标（xQZ ，yQZ）则由分角线方位角αJ2—QZ 和矢距E计算得到，其中分角线方位角αJ2—QZ 由第一条切线的方位角和线路转角求得：

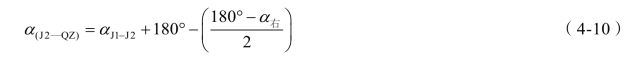
（2）计算圆心坐标。

如图4-5（a）所示，因ZY点至圆心方向与切线方向垂直，其方位角为

则圆心O坐标（xO，yO）为：

（3）计算圆心至各细部点的方位角。

如图4-5（b）所示，设ZY点至曲线上某细部里程桩点的弧长为li（li=细部点桩号里程-ZY点里程），其所对应的圆心角：

则圆心O至各细部点的方位角αOi—为：

（4）计算各细部点的坐标。

根据圆心坐标、圆心至细部点的方位角和半径，可以计算各细部点坐标：

【例4-4】如图4-5（a），该圆曲线半径R=500 m，转角（右）α右=12°52′48″，交点JD2的桩号为K2+560.976，JD1坐标为（261 936.955，341 250.715）、JD2坐标为（262 836.025，342 610.158），计算各主点坐标和各里程桩点的坐标。

【解】（1）计算主点坐标。

计算JD2至各主点（ZY、QZ、YZ）的坐标方位角，再根据坐标方位角和算出的测设元素切线长度T、外矢距E，用坐标正算公式计算主点坐标，计算结果见表4-2。

表4-2　圆曲线主点坐标计算

（2）计算圆心坐标。

计算ZY点至圆心的方位角为146°31′17″，计算圆心坐标为（262 387.847，342 838.897）。

（3）计算各细部点坐标。

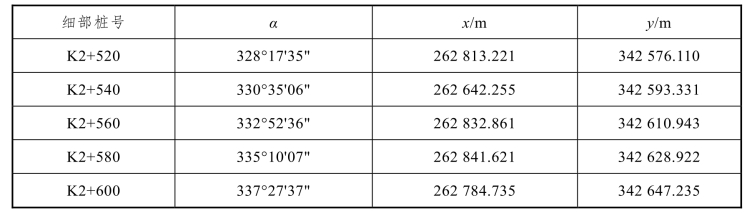
起点ZY点桩号=K2+560.976-56.437=K2+504.539，首先根据各细部点的里程，算出弧长，然后按上述公式计算圆心至各细部点的方位角αOi—，再计算各点坐标，计算结果见表4-3。

表4-3　圆曲线细部桩点坐标

在公路或铁路施工测量时，通常利用编程计算器（如卡西欧5 800）或计算机自编程序计算，具有速度快、精度高、准确性高等特点，可在野外快速计算出曲线上任意桩号的中桩坐标。利用全站仪按极坐标法施测，极大地提高了工作效率。

4.2.3.4　GPS-RTK法

用GPS-RTK放样曲线的工作与RTK放样点的方法相同，如果圆曲线各点的坐标是已知数据，则可按放样点的方法进行曲线放样。如果不知道曲线坐标，可以将曲线已知条件输入手簿，由手簿解算主点和细部点的坐标进行放样。南方RTK所提供的解算软件是按一定的里程进行坐标解算的，待坐标解算完毕后就可按点的放样方法进行放样。