地形图的基本应用技巧

2.4.2.1　求图上一点坐标

利用地形图进行规划设计，经常需要知道设计点的平面位置，它可根据图廓坐标格网的坐标值求出。如图2-18所示，欲确定图上P点坐标，首先绘出坐标方格abcd，过P点分别作x、y轴的平行线与方格abcd分别交于m、n、f、g，根据图廓内方格网坐标可知

图2-18　1∶2 000图坐标网格

再按测图比例尺（1∶2 000）量得dm、dg的实际平长度

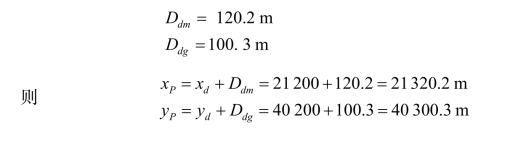
如果为了检核量测的结果，并考虑图纸伸缩的影响，则还需量出ma和gc的长度。若（dm+ma）和（dg+gc）不等于坐标格网的理论长度l（一般为10 cm），即说明图纸发生变形。此时，为了精确求得P点的坐标值，应按下式计算

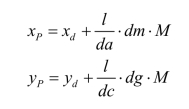
式中：M——地形图比例尺的分母。

2.4.2.2　求图上一点的高程

对于地形图上一点的高程，可以根据等高线及高程注记确定。如该点正好在等高线上，可以直接从图上读出其高程，例如图2-19中q点高程为64 m。如果所求点不在等高线上，可根据相邻等高线间的等高线平距与其高差成正比例原则，按等高线勾绘的内插方法求得该点的高程。如图2-19所示，过p点作一条大致垂直于两相邻等高线的线段mn，量取mn的图上长度dmn，然后再量取mp中的图上长度dmp，则p点高程

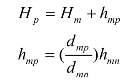
式中：hmn=1 m，为本图幅的等高距；dmp=3.5 mm；dmn=7.0 mm。则

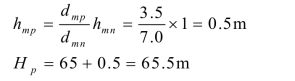
图2-19　地形图上求点的高程

2.4.2.3　求图上两点间的水平距离

若精度要求不高，可用毫米尺量取图上P、Q两点间距离，然后再按比例尺换算为水平距离，这样做受图纸伸缩的影响较大。

为了消除图纸变形的影响，首先，求出图上P、Q两点的坐标（xP，yP）、（xQ，yQ），如图2-18所示。然后，应根据两点的坐标计算水平距离，即按下式计算水平距离DPQ：

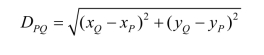
2.4.2.4　确定图上直线的坐标方位角

如图2-20所示，欲求直线AB的坐标方位角。首先求出图上A、B两点的坐标（xA，yA）、（xB，yB），然后，按照反正切函数，计算出直线AB坐标方位角，即

当直线AB距离较长时，按上式可取得较好的结果。

如果精度要求不高，也可以用图解的方法确定直线坐标方位角。首先过A、B两点精确地作坐标格网X方向的平行线，然后用量角器量测直线AB的坐标方位角。同一直线的正、反坐标方位角之差应为180°。(www.xing528.com)

图2-20　确定图上直线坐标方位角

2.4.2.5　确定直线的坡度

设地面两点m、n间的水平距离为Dmn，高差为hmn，则直线的坡度i为其高差与相应水平距离之比：

式中：Dmn为地形图上m、n两点间的长度（以毫米为单位）；M为地形图比例尺分母。坡度i常以百分率表示。例如，图2-19中m、n两点间高差为hmn=1.0 m，量得直线mn的图上距离为7 mm，并设地形图比例尺为1∶2 000，则直线mn的地面坡度为i=7.14%。

2.4.2.6　根据地形图绘制指定方向的断面图

在工程设计中，经常要了解在某一方向上的地形起伏情况，例如公路、隧道、管道等的选线，可根据断面图设计坡度，估算工程量，确定施工方案。如图2-21所示，绘制AB方向的断面图方法如下：

（1）在AB线与等高线交点上标明序号，如图2-21（a）中的1、2…10各点。

（2）如图2-21（b）所示，绘一条水平线作为距离的轴线，绘一条垂线作为高程的轴线。为了突出地形起伏，选用高程比例尺为距离比例尺的5倍或10倍。

（3）将图2-21（a）中1、2…10各点距A点的距离量出，并转绘于（b）图的距离轴线上。转绘时，一般情况下，断面图采用的距离比例尺与（a）图上用的比例尺一致，必要时也可按其他适宜比例尺展绘。

（4）在图2-21（b）的高程轴线上，按选定的高程比例尺及AB线上等高线的高程范围，标出66～72 m高程点。

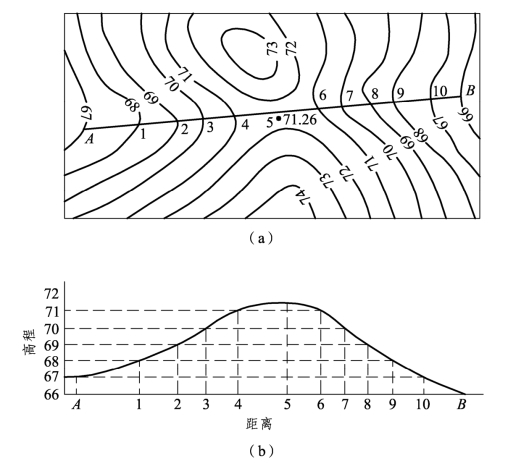
图2-21　绘制AB方向的断面图

（5）在图2-21（b）上，对应横坐标上A、1、2…10、B各点，在纵坐标上按高程比例尺取点，即得断面上的点，其中第5点为落在鞍部处实测碎部点，高程为71.6 m。

（6）将所得断面上相邻各点以圆滑曲线相连，即得AB方向的断面图。

2.4.2.7　按规定坡度在地形图上选定最短路线（图2-22）

图2-22　在地形图上选线

在做铁路、公路、管道等设计时，要求有一定的限制坡度。例如，要求在地形图上按规定坡度选择最短路线。其方法如下：

在图2-22中，要求自A点（高程38.0 m）向山头B点（高程45.36 m）修一条路，允许最大坡度i为8%，地形图比例尺为1∶1 000，等高距h为1 m，则路线跨过两条等高线所需的最短距离D可用坡度公式i=h/D导出，D=h/i=1/0.08=12.5m ，化为图上长为d=12.5m/1000=12.5mm。以A为圆心，d为半径画弧交39m等高线于1点；再以1点为圆心，d为半径画弧交40 m等高线于2点；以此类推得3、4、5、6、7点。至此两条路线均尚未到达B点。但是，由于B点高程为45.56 m，与7或7′点所在等高线高程之差为0.56 m，按8%坡度所需的最短实地距离0.56m/0.08=7m，相应图上距离为7 mm，而图上7′B与7B量得距离都大于最短距离7 mm，因此，这两条路均符合要求。

按上述方法选择路线，仅从坡度不超过8%来考虑。实际选线时，还须考虑其他因素，如地质条件、工程量大小、占用农田等，需对这些问题作综合分析，才能最后确定路线。

2.4.2.8　在地形图上确定汇水面积

在公路、铁路的勘测设计中，遇有跨越河流、山谷或深沟时，需要修建桥梁和涵洞。桥梁的跨度、涵洞的孔径与水流量有关，水量的大小又与该区域内汇集雨水和雪水地面面积的大小有关。某处能汇集到雨（雪）水的范围面积称为汇水面积，其大小与该地区的降雨（雪）量有关，这就为工程设计提供了有关水量的依据。为了确定汇水面积的范围，须在地形图上画出汇水面积的边界，这个边界实际上是一系列分水线即山脊线的连线。汇水面积边界线的特点是：边界线是通过一系列山脊线连着各山头及鞍部的曲线，并与河道的指定断面形成闭合环线。如图2-23所示，A处为公路跨越山谷的一座桥，桥的设计应考虑通过A处的流量，该处的汇水面积界线为从桥的西端起，经B、C、D、E、F、G、H回到桥的东端，形成汇水面积界线。

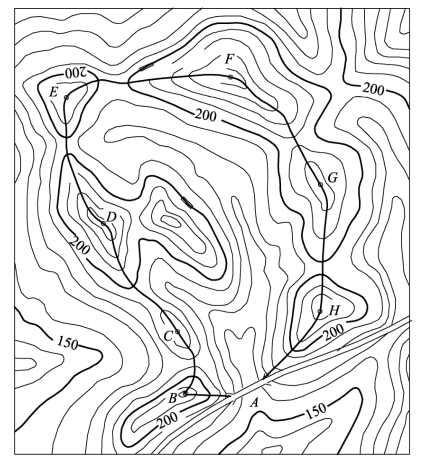
图2-23　在地形图上确定汇水面积