小波变换理论及其仪器功能的数学模型

小波变换是将原始信号与小波基进行内积运算，而快速小波变换是将内积运算转换为信号和离散滤波器的卷积运算，快速小波变换中的小波基的选择转化为正交镜像滤波器（QMF）的选择。

事实上，为了实现快速小波变换，只需要正交镜向滤波器组：H、G、H^∗和G^∗，而不必进行滤波器的多分辨率分析，因为滤波器与尺度参数j无关。H为低通分解滤波器，离散形式记为h（n）；G为高通分解滤波器，离散形式记为g（n）；H^∗为低通重构滤波器，离散形式记为rh（n）；G^∗为高通重构滤波器，离散形式记为rg（n）。滤波器组与尺度函数ϕ（t）和小波函数ψ（t）有关，据多分辨率框架理论，存在一个双尺度关系式：

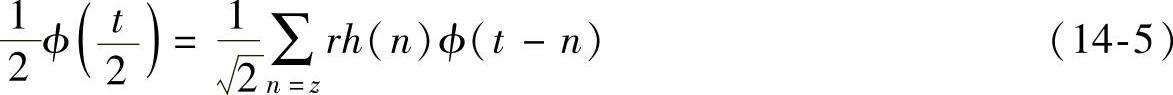
对于一个已知的小波基，它的尺度函数和小波函数也为已知，根据式（14-5）可得低通重构滤波器rh（n）。其他三个滤波器可由下面式子求得

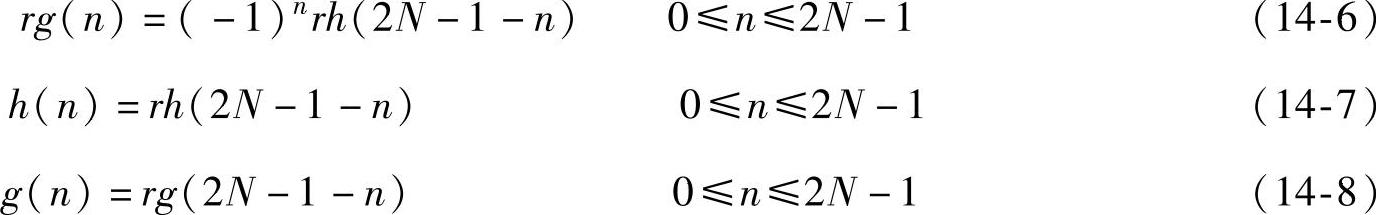
正交镜像滤波器组有两类：正交和双正交。正交是指低通分解滤波器H和高通分解滤器G正交，低通重构滤波器H^∗和高通重构滤波器G^∗正交；双正交是指低通分解滤波器H和高通重构滤波器G^∗正交，低通重构滤波器H^∗和高通分解滤波器G正交。常用的几个正交小波基有Daubechies小波、Beylkin小波、Coifman小波及插值样条小波，它们的rh（n）序列见相关文献。

1.快速小波分解

对于一个已知长度为N的离散原始信号样本f（k），最多可进行log₂N次分解。将样本f（k）与低通分解滤波器h（n）进行卷积滤波，下抽样即保留偶数下标样本后，得离散逼近系数cA₁；将样本f（k）与高通分解滤波器g（n）进行卷积滤波，下抽样即保留偶数下标样本后，得离散细节系数cD₁。这就是信号的第一次小波分解。

设信号的第j次分解的离散逼近系数为cA_j，则计算第j+1次的cA_j+1和cD_j+1的程序流程图如图14-26所示。

图14-26 第j+1次分解过程程序流程图

设最大分解次数为J，则0≤j＜J，其中当j=0时，cA₀=f（k）。由于实施了下抽样，使得j+1次的样本点数是j次的样本点数的一半，相当于样本的采样频率f_s减半。由于h（n）、g（n）与尺度参数j无关，为保持样本的采样频率与小波基的采样频率一致性，固定样本采样频率f_s不变，伸展信号的固有频率f₀，这样，保证了数值计算的可行性，这主要是由尺度函数ϕ（t）和小波函数ψ（t）的一些特性所决定的。不难从下面的信号表达式看出

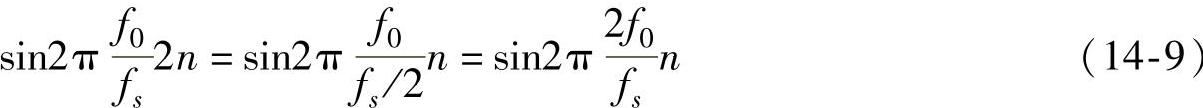
2.快速小波重构(www.xing528.com)

上述分解只是求得离散逼近系数cA_j（0＜j≤J）和离散细节系数cD_j（0＜j≤J），要求得离散逼近A_j（0＜j≤J）和离散细节信号D_j（0＜j≤J），需进行小波重构。重构的程序流程图如图14-27所示。

图14-27 第j次重构过程程序流程图

其中上抽样采用经典的内插法实现，即在相邻两个样本之间插入一个零值，以扩展样本长度。这样

A_J+D_J+D_J-1+…+D₂+D₁=f（k） （14-10）

上述实现过程包括三个方面的内容：首先把原始信号分解得到不同分辨率的小波系数，再修正这些系数，最后从这些系数合成不同分辨率分解分量、逼近分量和原始信号的重构。可见快速小波变换的实质是把原始信号不同频率段的信息抽取出来，并将其显示于时间轴上，这样既可反映信号的时域特征，也可反映信号的频域特征。小尺度高分辨率的变换包含信号的高频成分，大尺度低分辨率的变换包含信号的低频成分。这样，实际应用中可根据需要，择取不同尺度的变换来描述信号的特征。

3.小波包分解

小波包分解与小波分解的区别可用图14-28来表示。

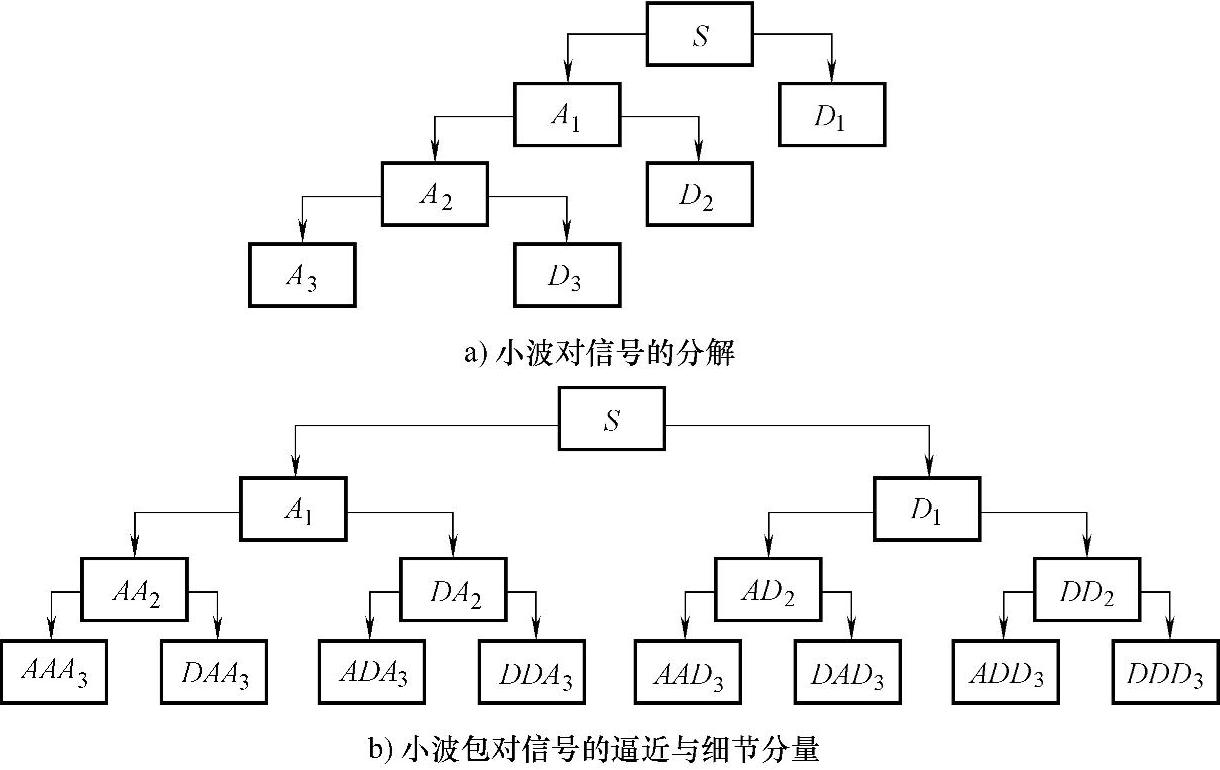
图14-28 小波分解与小波包分解的区别

图14-28a所示为小波对信号的分解，第一次分解将信号频带划分成高低两个频带A₁和D₁，第二次分解将第一次分解得到的低频段，即逼近分量A₁继续分解成A₂和D₂，如此依次类推，可以分解得到很多层（图中只画到第3层）。容易理解，不同层次具有不同频率分辨率。层次越往下，频率分辨率越高。根据测不准原理，层次越往下，时间分辨率越高。小波分析是从高层到低层只取分解后的高频分量，即图中的D₁，D₂，…。这样构成的滤波器组具有等Q特性。

如上所述，小波分解的各层具有不同的分辨率，但组合成滤波器组时，每一层所取的子带是固定的，因而在信号特性适应性方面还不够灵活。小波包分解则不一样，如图14-28b所示，它是将每一层所有滤波器子带均一分为二，并传至下一层。各层滤波器子带的数目为：第一层两个，第二层四个，第三层八个。每一层的滤波器子带都覆盖信号所占有的频率，只是各层的频率分辨率不同，组合而成的滤波器组其特性应覆盖整个频带，但滤波器子带间在频域上也不应该有重叠。因此，小波包分解多少层，以及在各层选择哪些子带来使用，都是十分灵活的。就是说，对不同特性的信号，可以构成相应的“最佳”滤波器组。在滤波器组的构造上，小波包分解提供了层间多种组合选择的可能性。