快速傅里叶变换和卷积算法的程序设计

在对测试分析仪器的功能进行编程之前，先要将仪器的功能分解成一些基本的功能单元，将这些功能单元规范化为一个个功能模块，并建立相应的功能数学模型，依据数学模型设计相应算法。

算法需要用一种语言来描述，同时，算法可有各种描述方法以满足不同的需求。采用结构化程序设计的方法进行算法的描述，描述算法的两个通用工具是流程图和伪代码。流程图图形化地描述了算法内部解决问题的逻辑，伪代码由解释语句组成，以段落的形式描述了处理的步骤。在对算法进行设计时常采用结构图，结构图的作用是在算法设计中给出算法各部分的关系，算法的每个部分称为一个模块，将算法分成部分或模块的过程，称为模块化。这种方法的本质是对复杂的问题采取抽象策略，通过把复杂算法进行分解，进入下一个抽象层次，这样精化过程一直继续，直到该算法可以用程序语言比较简单地实现。

设计算法，应达到以下目标：

1）正确性。算法应当满足具体功能的需求，否则，算法的正确与否的衡量标准就不存在了。算法程序对于一切合法的输入数据都能产生满足规格说明要求的结果。

2）可读性。可读性好有助于人对算法的理解，并且晦涩难懂的程序易于隐藏较多错误，难以调试和修改。

3）健壮性。当输入数据非法时，算法也能适当地作出反应或进行处理，而不会产生莫明其妙的输出结果。

4）高效性。效率指的是算法执行的时间。对于同一个功能如果有多个算法可以解决，执行时间短的算法效率高，特别是在实时处理的场合，算法的高效性尤为重要。

5）低存储量。存储量指算法执行过程中所需要的最大存储空间，占用存储空间越少的算法越好，一般程序设计中尽量采用动态分配和释放存储空间，以满足算法的低存储量需要。

下面以快速傅里叶变换（FFT）算法程序设计及卷积算法程序设计为例进行说明。

1.快速傅里叶变换（FFT）算法程序设计

在动态信号分析中，很多分析功能是以离散傅里叶变换为基础，简称DFT，其数学模型如下

正变换：

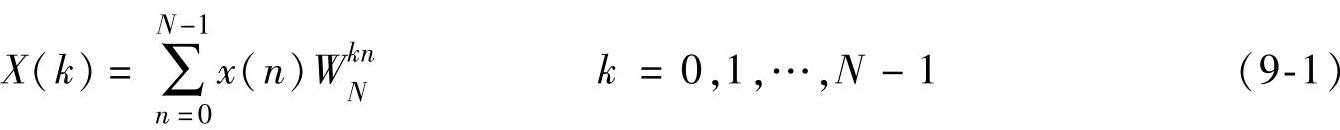
逆变换：

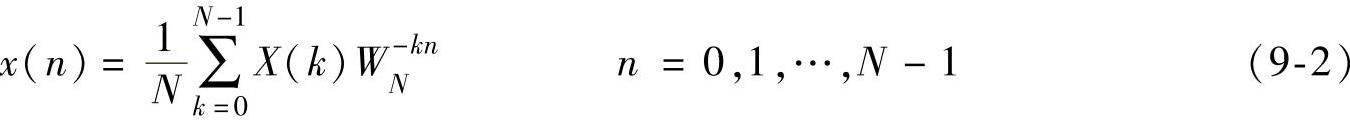
式中，

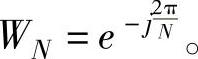
然而，当数据有较长的长度时，这种变换的计算量是很大的，在一定程度上限制了信号分析的发展与应用。1965年J·W·Cooly和J·W·Tukey发表了他们的DFT快速算法之后，快速傅里叶变换（FFT）算法迅速发展起来，产生了基2FFT、基4FFT、基8-4-2FFT等几种算法，这些算法大大地加快了傅里叶变换的运算速度。采用速度相对较快的混合基FFT即基8-4-2FFT算法，运用运行速度快的汇编语言编制出了FFT程序。基8-4-2FFT保持了基2FFT的次序和对称性，但省去了对实序列的多余运算，因此在计算和存储量上有减少一半的效果。基8-4-2FFT程序尽可能多地进行基8迭代，然后，如有必要，也可以进行基4或基2迭代，其程序流程图如图9-7所示。

2.卷积算法程序设计

如果两序列x（n）和h（n）的长度分别为N和M，即

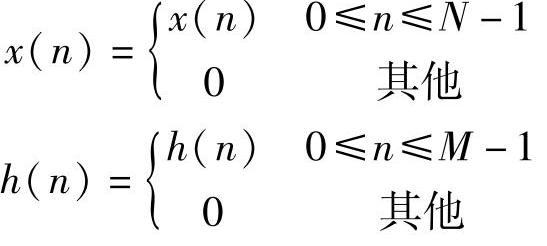(www.xing528.com)

两序列x（n）和h（n）的卷积数学模型为

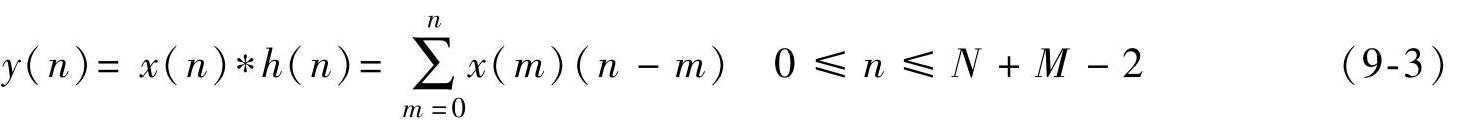
m=0

式（9-3）表明，线性卷积计算过程很繁琐，当x（n）的样本点N较大时，无论是计算时间或是计算所需存储量，都会很大，为克服这些困难，采用快速傅里叶变换（FFT）计算线性卷积。

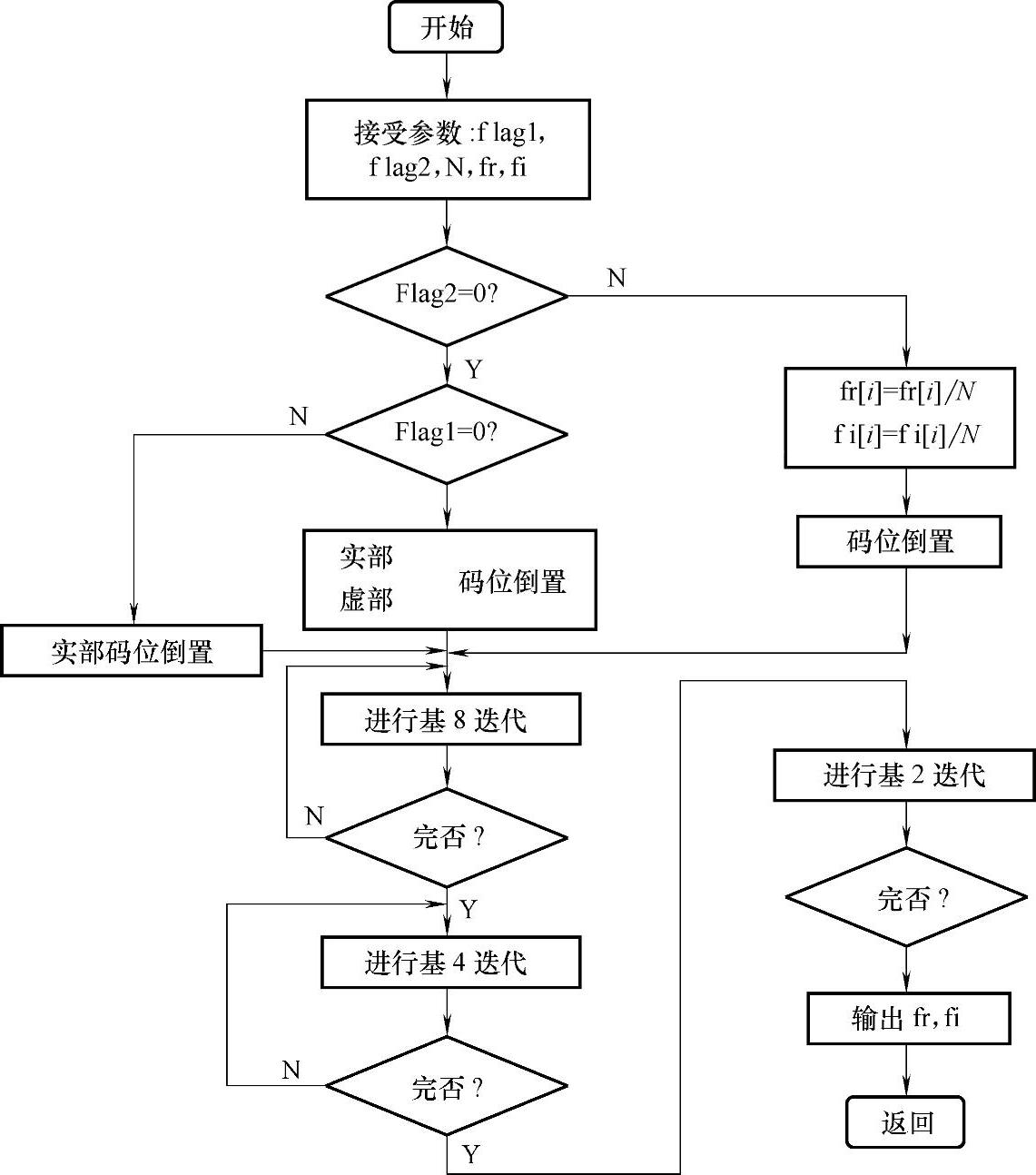
图9-7 基8-4-2FFT程序流程图

采用伪代码来描述FFT计算线性卷积的过程，步骤如下：

1）令L≥N+M-1，将x（n）延长至L，后L-N个补充为零，将h（n）延长至L，后L-M个元素补充为零，为满足FFT的需要，L还应为2的幂。

2）计算X（k）=FFT[x（n）]和H（k）=FFT[h（n）]。令Y（k）=X（k）·H（k）

则 y（n）=IFFT[Y（k）]

只要进行二次FFT，一次逆变换（IFFT）就可以完成线性卷积运算。

但上述方法适用于x（n）和h（n）两序列长度比较接近或者相等情况，如果两者长度相差较大，例如h（n）为某滤波器单位冲激响应，长度有限，用来处理一个很长的信号x（n），这样按上述方法，h（n）后补许多零之后再计算，运算时间不但不会减少，反而会增加。

为了解决这个问题，可以将x（n）分为许多小段，每小段长度为h（n）的长度接近，把x（n）的每小段与h（n）作线性卷积，最后取和，这种方法叫“重叠相加法”。

设x（n）和h（n）均为因果序列，h（n）长度为M，x（n）长度为N₁，且N₁M。将x（n）分成若干小段，每段长为N，设x_i（n）表示第i段序列。

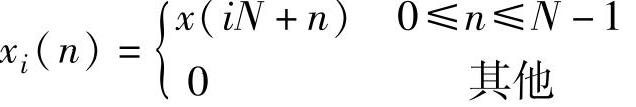
将x_i（n）和h（n）补零延长到L=N+M-1，当M值给定时，只有改变N值以满足L为2的幂的需要。这样

y_i（n）=x_i（n）∗h（n）=x_i（n）h（n） （9-4）

值得注意的是，y_i（n）长为N+M-1，而x_i（n）的有效长度为N，故相邻的y_i（n）必有M-1长度重叠，最后必须对重叠部分求和，重叠部分相加可由以下关系式计算出来。

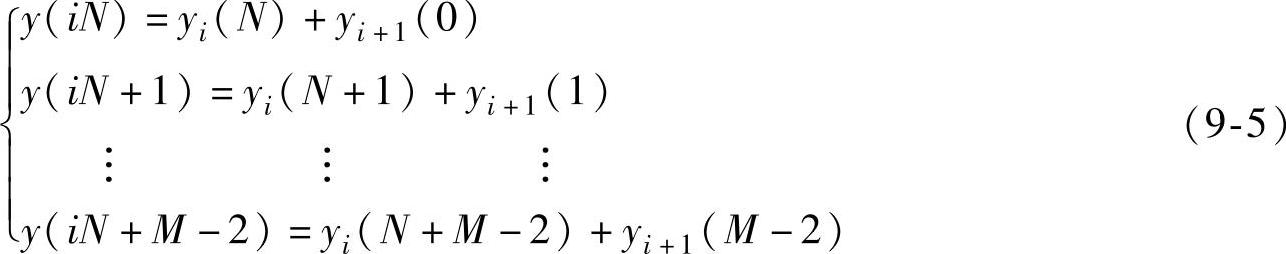
将y_i（n）最后M-1项与y_i+1（n）最开始的M-1项相加起来得到y（iN）、y（iN+1）、…、y（iN+M-2）各项。