图形变换的数学模型及应用

为了便于观察、显示虚拟仪器的分析结果，常常需要进行图形变换，为此在显示建模中需要建立许多图形变换的数学模型。

1.窗口变换

在显示器的显示中常常需要通过矩阵变换将原始数据转化为适合显示器显示的数据，这一过程就是窗口变换，其数学模型为

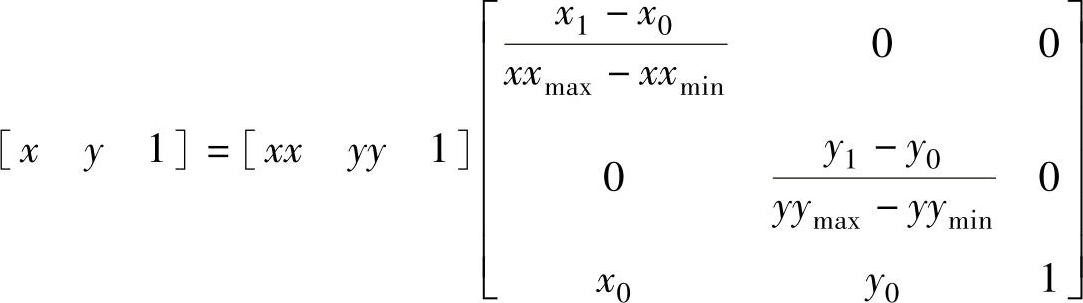
其中，[xy 1]为数据在显示窗口中的齐次坐标；[xxyy 1]为数据在原始直角坐标系中的坐标；x₀，y₀，x₁，y₁分别为显示区域相对于显示器的偏移坐标；xx_max，xx_min，yy_max，yy_min为原始数据序列xx（n）、yy（n）的极值。这里显示器窗口的坐标原点建立在显示器显示区域的左下角，x轴向上，y轴向右，下同。

2.二维缩放

二维缩放包括两种缩放方式，即无极缩放和框选缩放。

（1）无极缩放 所谓无极缩放是指可以以任意缩放比例逐步缩放、细化，达到满足科学观察和研究的目的。可采用如下方法：在需要细化的区域，按下鼠标左键，向不同区域移动鼠标，再单击鼠标，即可确定缩放中心和缩放倍数，无极缩放如图7-30所示。

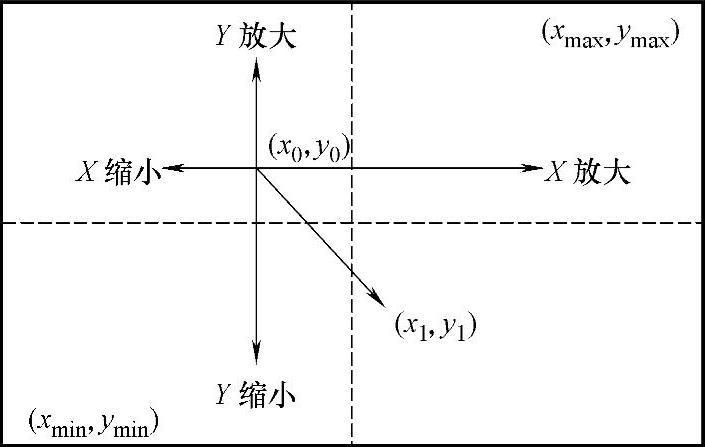
图7-30 无极缩放

无极缩放的数学模型如下

其中，[xy 1]为缩放后的齐次坐标；[xxyy 1]为缩放前的齐次坐标；（x₀，y₀）为第一次按下鼠标时的坐标；（x₁，y₁）为第二次按下鼠标时的坐标，x_min、x_max、y_min、y_max为缩放前显示区的最大值和最小值。

（2）框选缩放 框选缩放是一种常用的放大细化方式，它较无极缩放简单，只是将选中的区域满屏显示。其数学模型如下

其中，（xx_min，yy_min），（xx_max，yy_max）为显示区的最值，而（x_min，y_min），（x_max，y_max）为框选区的最值。

3.三维图形的任意角度旋转(www.xing528.com)

三维图形的旋转分为绕x轴，绕y轴，绕z轴或绕任意直线旋转，绕任意直线的旋转可由绕x轴，绕y轴，和绕z轴的旋转组合而成。

三维图形绕z轴正向旋转θ角的数学模型为

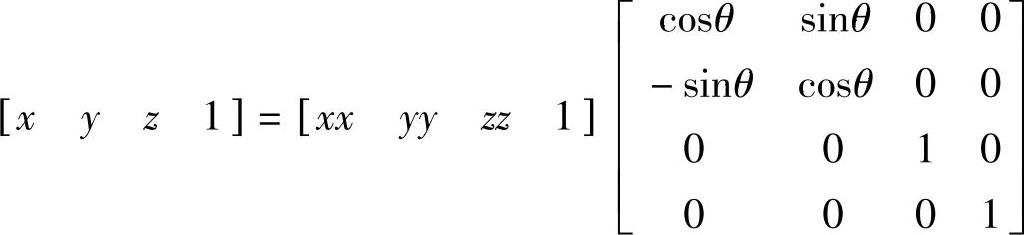
绕x轴正向旋转θ角的数学模型为

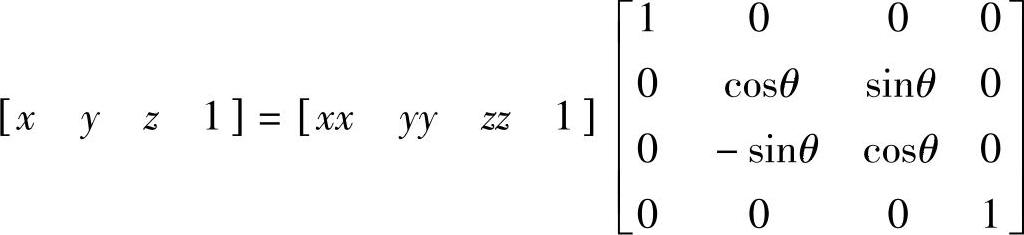
绕y轴正向旋转θ角的数学模型为

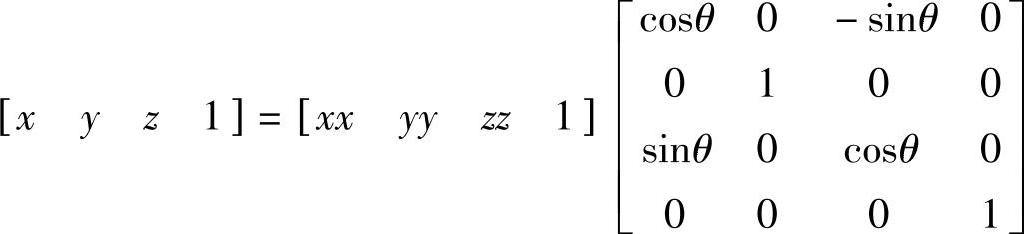
4.三维图形的缩放

三维图形缩放的数学模型如下

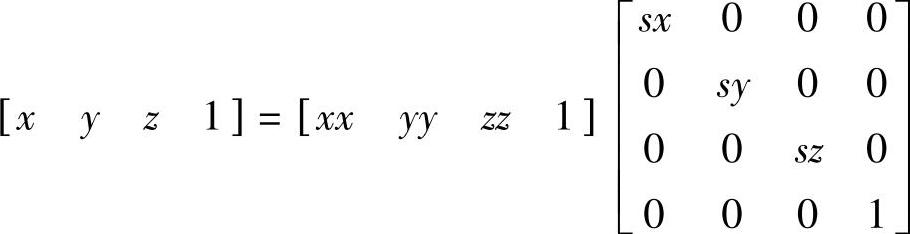
其中，sx，sy，sz分别为三维图形沿x，y，z轴方向缩放的倍数。

5.三维图形的平移

三维图形平移的数学模型如下

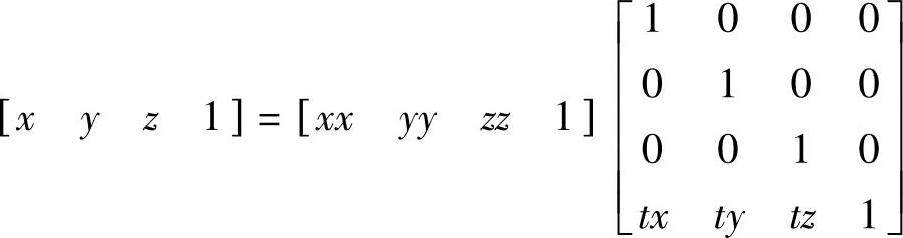
其中，tx，ty，tz分别为三维图形沿x，y，z轴方向的位移。