【摘要】:温度计的几何模型比较容易建立,关键在于建立体现其真实感的物理模型。温度计的坐标系建立如图7-8b所示,即控件坐标系的原点建立在圆柱体的中心,y轴向右,z轴向上,x轴垂直于显示器向外。温度计的三维几何模型上半椭球:圆柱体:下半椭球:图7-8 温度计及其建模其中,R表示圆柱体或上、下半椭球的x、y向半径;He表示上、下半椭球的z向半径;H表示圆柱体的高。
温度计如图7-8a所示,将一个圆柱体的上、下底面分别与一个上、下半椭球结合起来,即得到温度计。
温度计的几何模型比较容易建立,关键在于建立体现其真实感的物理模型。
温度计的坐标系建立如图7-8b所示,即控件坐标系的原点建立在圆柱体的中心,y轴向右,z轴向上,x轴垂直于显示器向外。
(1)温度计的三维几何模型
上半椭球: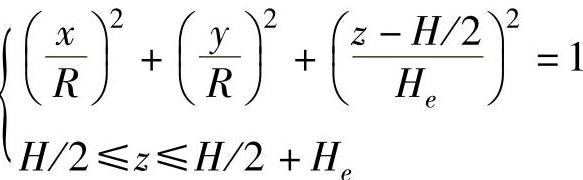
圆柱体: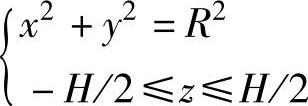
下半椭球: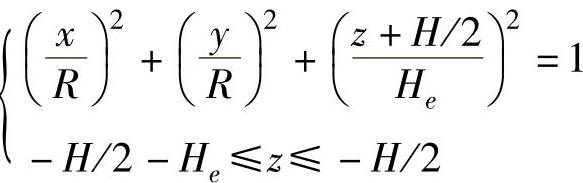
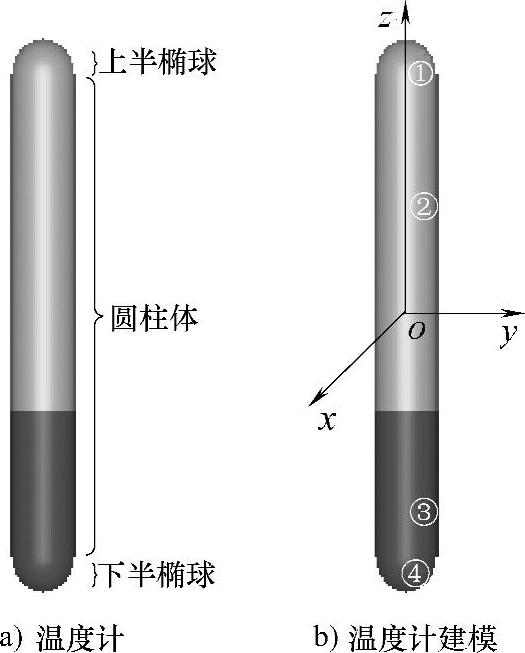
图7-8 温度计及其建模
其中,R表示圆柱体或上、下半椭球的x、y向半径;He表示上、下半椭球的z向半径;H表示圆柱体的高。
(2)温度计的二维几何模型
基本图形:
半椭圆: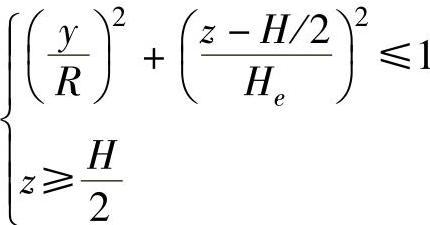
长方形: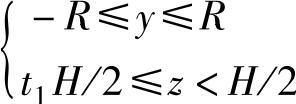
其中,z=t1H/2为水银柱的液面位置;-1≤t1≤1,
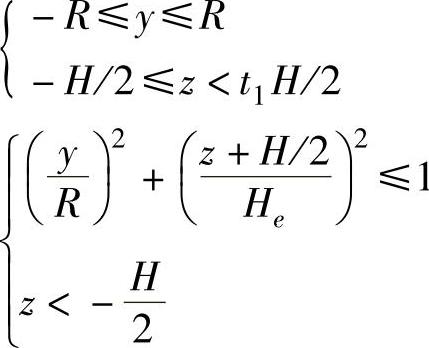
(3)温度计的物理模型
基本图形:(https://www.xing528.com)
Color(y,z)=RGB(L,V,N(y,z),Ia,Ka,Id,K1d,Ks=K1d,n)
其中,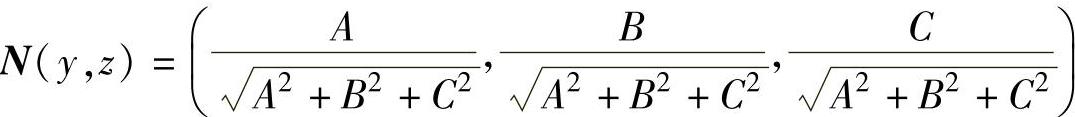
而
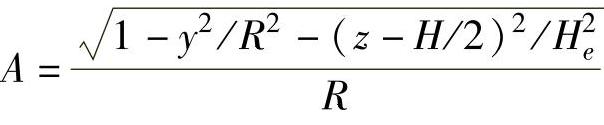 ,
,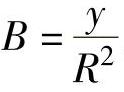 ,
,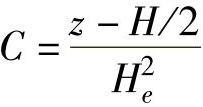
Color(y,z)=RGB(L,V,N(y,z),Ia,Ka,Id,K1d,Ks=K1d,n)
其中,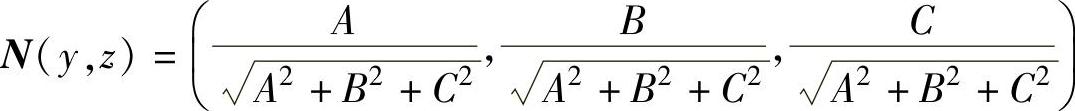
而
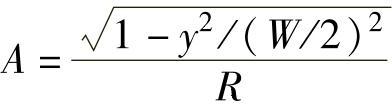 ,
,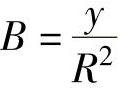 ,C=0,
,C=0,
Color(y,z)=RGB(L,V,N(y,z),Ia,Ka,Id,K2d,Ks=K2d,n)
其中,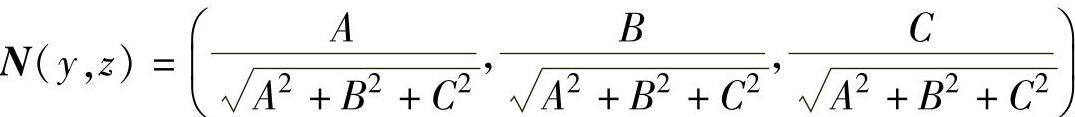
而
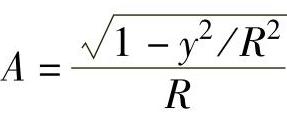 ,
,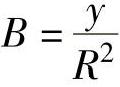 ,C=0,
,C=0,
Color(y,z)=RGB(L,V,N(y,z),Ia,Ka,Id,K2d,Ks=K2d,n)
其中,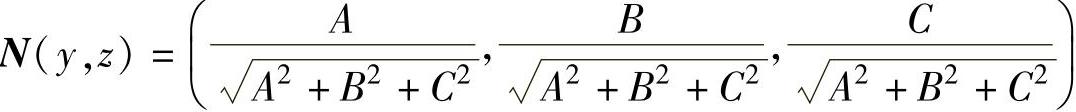
而
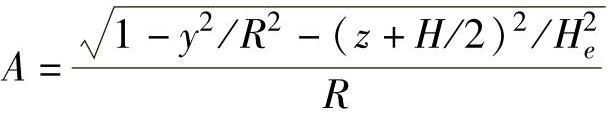 ,
,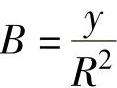 ,
,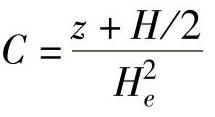
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




