虚拟旋钮模型设计优化

旋钮如图7-1a所示，在一个由圆环和半球体所组成的立体图形上，绘上表示指针和刻度的线段，即得到旋钮。如图7-1b所示，将控件坐标系的原点建立在圆环的中心，y轴向右，z轴向上，x轴垂直于显示器向外，则旋钮中半球体的数学模型为

圆环的数学模型为

式中，R为旋钮的包括刻度在内的半径，0＜t₁＜t₂＜1。

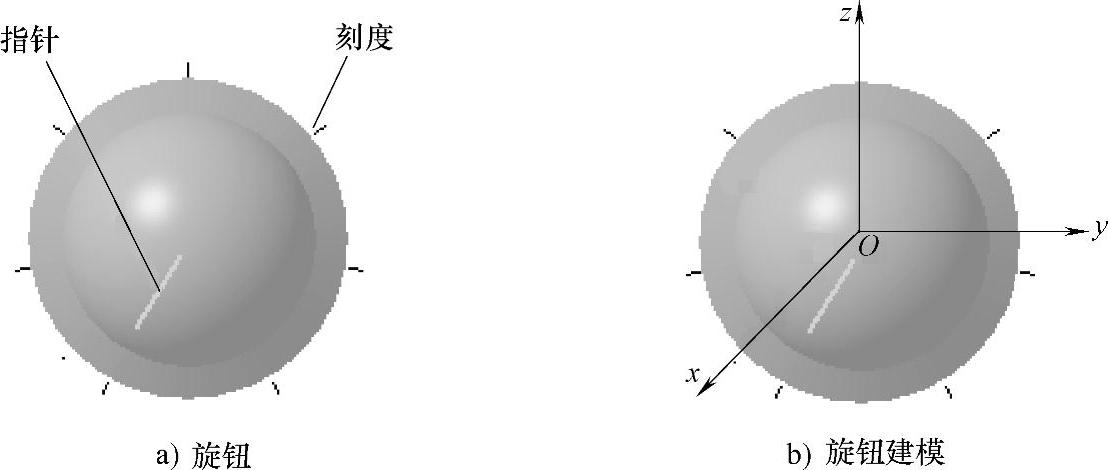
图7-1 旋钮及其建模

通过投影变换得到虚拟旋钮的如下二维几何模型：

1）圆（半球体的投影）：y²+z²≤（t₁R）²

2）圆环：（t₁R）²＜y²+z²≤（t₂R）2

刻度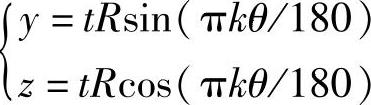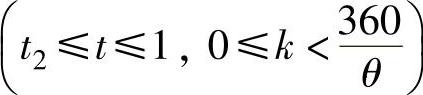：，，其中，k表示第k条刻度，（k=0对应垂直向上的刻度）；θ为每两个刻度间沿顺时针方向的夹角（单位：（°））。

指针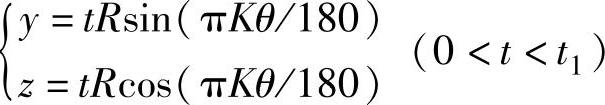：，其中，K表示指针指向第K条刻度。(www.xing528.com)

为了使虚拟旋钮看起来具有真实感，需要建立其物理模型，即确定虚拟旋钮上每一点的光强度，尤其是控件的二维几何模型上每一点的光强度Color（y，z）。物体上任意一点的光强度与光源的单位方向向量L、单位视向向量V、单位法向向量N、环境光强I_a、环境光的反射系数K_a、光源强度I_d、漫反射系数K_d、镜面反射系数K_s、反射指数n有关，从而控件的二维几何模型上每一点的光强度也与L、V、N、I_a、K_a、I_d、K_d、K_s和n有关。如果记控件的二维几何模型上每一点所对应的三维几何模型的单位法向量为N（y，z），记

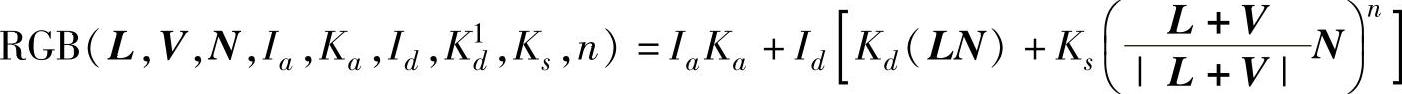
则可建立与虚拟旋钮的二维几何模型对应的光强度（或物理）模型如下

基本图形：Color（y，z）=RGB（L，V，N（y，z），I_a，K_a，I_d，K¹_d，K_s=K¹_d，n）

其中，

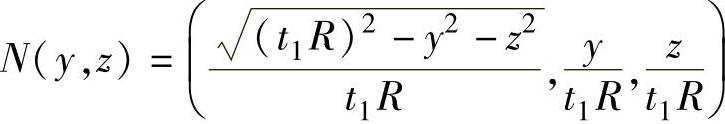
Color(y，z)=K¹_d×255。

刻度：Color（y，z）=K²_d×255

指针：Color（y，z）=K²_d×255

在以上物理模型中，K_a实际上反映了控件所在环境的颜色；K_d和K_s反映了控件的颜色。

以上对虚拟旋钮的建模原理、方法和过程进行了介绍。由建模过程可知，对虚拟控件的建模主要包括控件的三维几何模型、坐标系的建立、（通过投影变换得到的）二维几何模型和（与虚拟控件的二维几何模型对应的）物理模型四个部分，因此下面对每个虚拟控件的建模都只给出这四个部分的结果，而不再对建模过程作详细介绍。